- Article
- Open access
- Published:
Nature volume 645, pages 702–711 (2025)Cite this article
-
126k Accesses
-
8 Citations
-
908 Altmetric
Subjects
Abstract
Since the advent of computing, humans have sought computer input technologies that are expressive, intuitive and universal. While diverse modalities have been developed, including keyboards, mice and touchscreens, they require interaction with a device that can be limiting, especially in on-the-go scenarios. Gesture-based systems use cameras or inertial sensors to avoid an intermediary device, but tend to perform well only for unobscured movements. By contrast, brain–computer or neuromotor interfaces that directly interface with the body’s electrical signalling have been imagined to solve the interface problem1, but high-bandwidth communication has been demonstrated only using invasive interfaces with bespoke decoders designed for single individuals2,3,4. Here, we describe the development of a generic non-invasive neuromotor interface that enables computer input decoded from surface electromyography (sEMG). We developed a highly sensitive, easily donned sEMG wristband and a scalable infrastructure for collecting training data from thousands of consenting participants. Together, these data enabled us to develop generic sEMG decoding models that generalize across people. Test users demonstrate a closed-loop median performance of gesture decoding of 0.66 target acquisitions per second in a continuous navigation task, 0.88 gesture detections per second in a discrete-gesture task and handwriting at 20.9 words per minute. We demonstrate that the decoding performance of handwriting models can be further improved by 16% by personalizing sEMG decoding models. To our knowledge, this is the first high-bandwidth neuromotor interface with performant out-of-the-box generalization across people.
Similar content being viewed by others
Main
Interactions with computers are increasingly ubiquitous, but existing input modalities are subject to persistent trade-offs between portability, throughput and accessibility. While keyboard text entry, texting, trackpads and mice are important, our aim is to enable computation in settings in which these conventional methods are not feasible, for example, seamless input to mobile computing with smartphones, smart watches or smart glasses.
A neural interface that can obviate trade-offs and provide seamless interaction between humans and machines has long been sought, but has been slow to emerge. In recent years, intracortical neural interfaces that directly interface with brain tissue have advanced the premise2,5, demonstrating translation of thought into language at bandwidth rates comparable with conventional computer input systems3,4. However, existing high-bandwidth interfaces require invasive neurosurgery, and the models that translate neural signals to digital inputs remain bespoke.
Non-invasive approaches relying on recording of electroencephalogram (EEG)6 signals at the scalp have offered more generality across people, for example, for gaming7, but EEG can require lengthy setup, and the low signal-to-noise ratio of these devices has limited their use8.
Regardless of the modality, issues of signal bandwidth, generalization across populations and the desire to avoid per-person or session-to-session calibration remain key technical hurdles in the field of brain–computer interfaces (BCIs)5,9,10,11,12.
To build an interface that is both performant and accessible, we focused on an alternative class of non-invasive neuromotor interfaces based on reading out the electrical signals from muscles using electromyography (EMG). Myoelectric potentials are produced by the summation of motor unit action potentials (MUAPs) and represent a window into the motor commands issued by the central nervous system. Surface EMG (sEMG) recordings offer a high signal-to-noise ratio by amplifying neural signals in the muscle13, enabling real-time single-trial gesture decoding. The nature of the sEMG signal lends itself naturally to human–computer interface (HCI) applications because it is not subject to problems that vex computer-vision-based approaches, such as occlusion, insufficient lighting or gestures with minimal movement. Indeed, sEMG has been deployed for diverse applications in clinical settings14,15, for diagnosis and rehabilitation16, as well as prosthetic control1,17,18.
However, current EMG systems, including those for prosthetic control17, have many limitations for wide-scale use and deployment. Laboratory systems are generally encumbered with wires to external power sources and amplifiers, and placed over uncomfortable locations such as the target muscle belly. Commercially available EMG-based neuromotor interfaces have been historically challenging to control19, relating to myriad technical issues such as poor robustness across postures20, a lack of standardized data21, electrode displacement22, and a lack of both cross-session23 and cross-user generalization24. More recently, deep learning techniques have shown some success at addressing these limitations25, but a general lack of available EMG data and low sample sizes are believed to limit their efficacy21.
To validate the hypothesis that sEMG can provide an intuitive and seamless computer input that works in practice across a population, we developed and deployed robust, non-invasive hardware for recording sEMG at the wrist. We chose the wrist because humans primarily engage the world with their hands, and the wrist provides broad coverage of sEMG signals of hand, wrist and forearm muscles while affording social acceptability26,27. Our sEMG research device (sEMG-RD) is a dry-electrode, multichannel recording platform with the ability to extract single putative MUAPs. It is comfortable, wireless, accommodates diverse anatomy and environments and can be donned or doffed in a few seconds.
To transform sEMG into commands that drive computer interactions, we architected and deployed neural networks trained on data from thousands of consenting human participants. We also created automated behavioural-prompting and participant-selection systems to scale neuromotor recordings across a large and diverse population. We demonstrated the ability of our sEMG-RD to drive computer interactions such as one-dimensional (1D) continuous navigation (akin to pointing a laser-pointer based on wrist posture), gesture detection (finger pinches and thumb swipes) and handwriting transcription.
The sEMG decoding models performed well across people without person-specific training or calibration. In open-loop (offline) evaluation, our sEMG-RD platform achieved greater than 90% classification accuracy for held-out participants in handwriting and gesture detection, and an error of less than 13° s−1 error on wrist angle velocity decoding. On computer-based tasks that evaluate these interactions in closed-loop (online), we achieved 0.66 target acquisitions per second in wrist-based continuous control, 0.88 acquisitions per second on discrete gestures and 20.9 words per minute (WPM) with handwriting.
To our knowledge, this is the highest level of cross-participant performance achieved by a neuromotor interface. Our approach opens up directions of sEMG-based HCI research and development while solving many of the technical problems fundamental to current and future BCI efforts.
Scalable sEMG recording platform
To build generic sEMG decoding models capable of predicting user intent from neuromuscular signals, we developed a hardware and software platform capable of quickly and robustly coupling the neuromotor interface with computers across a diverse population (Fig. 1a). Consenting participants (Methods) were seated in front of a computer while wearing the sEMG-RD at the wrist; the sEMG-RD is a dry electrode, multichannel recording device with a high sample rate (2 kHz) and low-noise (2.46 μVrms), and is compatible with everyday use26,27 (Fig. 1a and Methods). We fabricated the device in four different sizes to ensure coverage across a range of wrist circumferences. The device streamed wirelessly over secure Bluetooth protocols and provided a battery life of more than 4 h.
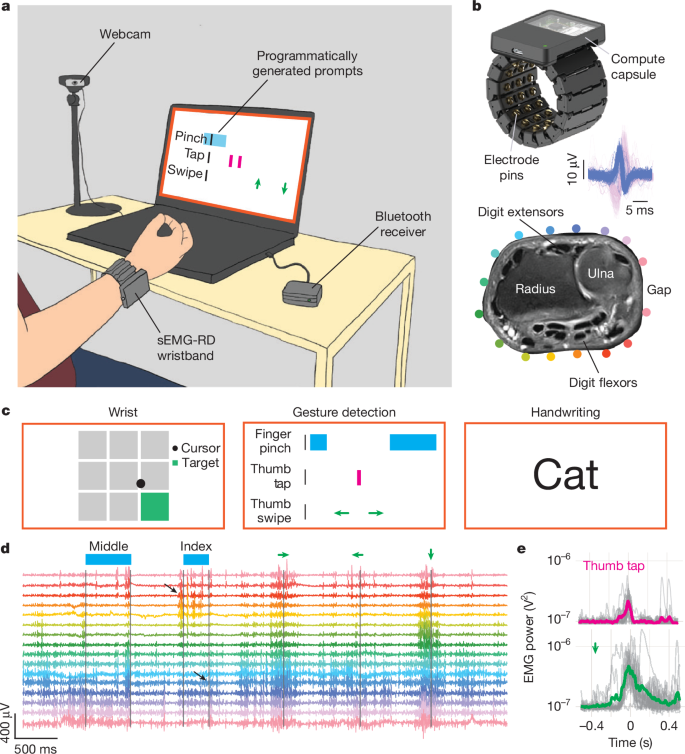
a, Overview of sEMG data collection. A participant wears the sEMG wristband, which communicates with a computer through a Bluetooth receiver. The participant is prompted to perform diverse movements of the hand and wrist. A webcam captures their hand and wrist, excluding the face. Between sessions within a single day, the participants remove and slightly reposition the sEMG wristband to enable generalization across different recording positions. b, The sEMG wristband consists of 48 electrode pins configured into 16 bipolar channels with the sensing axis aligned with the proximal–distal axis of the forearm and the remainder serving as shield and ground electrodes (top). A 3D printed housing encloses cabling and analogue amplifiers for each channel. A compute capsule digitizes the signal and streams sEMG data using Bluetooth. Inset: overlay of 62 and 72 individual instances of two putative MUAPs evoked by subtle thumb (blue) and pinky extension (pink) movements, respectively, from a single sEMG channel (Methods). Bottom, a proton-density-weighted axial plane magnetic resonance imaging (MRI) scan of the wrist; relevant bone and muscle landmarks are labelled. The coloured dots indicate the approximate position of electrodes, with an adjustable gap between electrodes placed over an area of low muscle density. c, Schematic of the prompters for the three tasks (Methods and Extended Data Fig. 4). In the wrist task, the participants controlled a cursor using wrist movements tracked in real time with motion capture. In the discrete-gesture task, gesture prompts scrolled from right to left. In the handwriting task, the participants wrote words presented on the screen. d, Representative sEMG signals, high-pass filtered at 20 Hz, recorded during performance of discrete gestures reveal intricate patterns of activity across multiple channels accompanying each gesture, with prompt timings above (for example, ‘middle’ indicates middle pinch, and the green left arrow indicates a leftward thumb swipe). Channel colouring corresponds to electrode locations in b. The black arrows highlight activation of flexors and extensors during an index-to-thumb pinch and release, respectively. e, Representative examples of variability in gestural sEMG activations across gesture instances (thumb taps (top) and downward thumb swipe (bottom)). The grey lines show the instantaneous high-pass-filtered sEMG power, summed across channels, for all instances of a gesture during a single band placement. The bold traces show the average. The mean was subtracted from all traces, and the power was offset by 10−7 V2 to plot on a logarithmic scale without visually exaggerating the baseline variance.
We optimized the sEMG-RD for recording subtle electrical potentials at the wrist (Extended Data Fig. 1). We manufactured the device in four sizes, with a circumferential interelectrode spacing of 10.6, 12, 13 or 15 mm, approaching the spatial bandwidth of EMG signals at the forearm (~5–10 mm)28, while minimizing the device’s form factor. We placed the gap in electrodes to allow for tightening adjustments along the ulna bone, where muscles are reduced in density. Together, this enabled the sensing of putative MUAPs across the wrist during low-movement conditions (Fig. 1b and Extended Data Fig. 2).
To collect training data for models, we recruited an anthropometrically and demographically diverse group of participants (162–6,627 participants, depending on the task; Extended Data Fig. 3) to perform three different tasks: wrist control, discrete-gesture detection and handwriting. In all cases, the participants wore sEMG bands on their dominant-side wrist and were prompted to perform actions using custom software run on laptops (Fig. 1c). For wrist control, the participants controlled a cursor, the position of which was determined from wrist angles tracked in real time using motion capture. During the discrete-gesture detection task, a prompter instructed participants to perform nine distinct gestures with a randomized order and intergesture interval. During the handwriting task, the participants were prompted to hold their fingers together (as if holding an imaginary writing implement) and ‘write’ the prompted text. Further training data protocol details are provided in the Methods.
We designed the data-collection system to facilitate supervised training of sEMG decoding models. During data collection, we recorded both sEMG activity and the timestamps of labels on the prompter using a real-time processing engine. We designed the engine to be used during recording and model inference to reduce online–offline shift (Methods). To precisely align prompter labels to actual gesture times, which may vary due to a participant’s reaction time or compliance, we developed a time-alignment algorithm that enabled post hoc inference of gesture event times (Methods).
Examination of raw sEMG traces revealed highly structured patterns of activity (Fig. 1d). Discrete gestures evoked patterned activity across a set of channels that roughly corresponded to the position of flexor and extensor muscles for the corresponding movement (Fig. 1d and Extended Data Fig. 1c). Fine differences in sEMG power across instances of a given gesture performed during a session (Fig. 1e) highlight the power of the platform in acquiring repeated time-aligned examples for supervised learning and some of the challenges facing generalization of EMG decoders.
Single-participant models do not generalize
It is well known across BCI modalities that both across-session and across-user generalization are difficult problems5,11,24,29. We wanted to evaluate the difficulty of these generalizations for sEMG decoders. Inspection of the raw data revealed pronounced variability in the sEMG for the same action across different participants and band donnings (which we refer to as sessions), reflective of variations in sensor placement, anatomy, physiology and behaviour that make generalization challenging (Fig. 2a,b). As an example of this variability, we found that the cosine distances between waveforms of the same gesture across sessions and users heavily overlapped with the distribution of distances between waveforms of different gestures (Extended Data Fig. 5a), and intermingled even in a nonlinear embedding of gesture distances (Fig. 2b), highlighting the challenge of the generalization problem.
a, Cross-participant (columns) and cross-session variability (light lines) in gestural sEMG for four discrete gestures (different rows and colours) across seven participants. Four of the possible nine gestures are shown for clarity. The light lines show the high-pass-filtered sEMG power averaged across all channels and all gesture instances during a single band placement. The bold lines correspond to the average across all band placements. b, t-SNE embedding of sEMG activations (Methods) across participants for the four different gestures in a. Gesture colour map as in a, with shading reflecting different participants (n = 20). Each dot reflects an individual gestural instance. c,d, Single-participant models trained and tested on the same participant (c) or different participants (d). Generalization across sessions improves as more training data are used. Generalization across participants remains poor even when more training data are used. Statistical analysis was performed using two-sided Wilcoxon signed-rank tests; all pairwise comparisons are significant; P < 10−10. n = 100 single-participant models. The boxes show the median (centre line) and lower and upper quartiles (box limits), and the whiskers extend to ±1.5 × interquartile range. e–g, The decoding error of models trained to predict wrist angle velocity (e), classify nine discrete gestures (f) and classify handwritten characters (g) as a function of the training set size. Data are the mean ± s.e.m. decoding error evaluated on a test set of held-out participants (n = 22 for wrist, 100 for discrete gestures and 50 for handwriting) (Methods). The dashed lines and inset equations show fitted scaling curves (N is measured in units of hundreds of participants and D in millions of parameters). For discrete gestures, the open circle represents varying numbers of sessions per participant (Methods).
To evaluate the ability of obtaining performant sEMG decoders across sessions for a given participant, we trained single-participant models for 100 participants who had collected at least five sessions on the discrete-gesture-classification task. For each participant, we held out one session for evaluation and then trained models on two, three or four of the remaining sessions (Methods). As an offline evaluation metric, we used the false-negative rate (FNR), defined as the proportion of prompted gestures for which the correct gesture was not detected by the model.
Single-participant models trained and tested on the same participant achieved offline performance that improved substantially with more training data (Fig. 2c). By contrast, models trained on one participant and then tested on another showed substantially worse performance and benefited only mildly from an increasing amount of training data (Fig. 2d), indicating a greater domain shift across people compared with across sessions. For 98% of participants, the model trained on their own data performed better compared with all other single-participant models (Extended Data Fig. 5b).
We wondered whether cross-participant generalization was difficult because there was structure or clusters across people, or whether every participant required a relatively unique single-participant model. The former could motivate an approach where a set of models trained on a small population (within each cluster) could achieve a high level of population coverage. The absence of overt structure in a t-distributed stochastic neighbour embedding (t-SNE; Extended Data Fig. 5c) of the average model transfer FNR between participant pairs suggests that there are no obvious participant clusters. Moreover, there are no people who exhibit the ability to generate performant models for other people, nor are there any people for whom other people’s models always perform well (Extended Data Fig. 5d).
Offline evaluation of generic models
To avoid the need to train and tune models for each individual, we trained generic models that are able to generalize to entirely held-out participants. To do this, we collected data from hundreds to thousands of data-collection participants for each task. These data were then used to train neural network decoding models. In each case, we used preprocessing techniques and network architectures designed for processing multidimensional time series (Methods and Extended Data Fig. 6): multivariate power frequency (MPF) features and a long short-term memory (LSTM) layer for the wrist task, a 1D convolution layer followed by an LSTM layer for the discrete-gesture task, and MPF features and a conformer30 for the handwriting task, which we anticipated would require an architecture with richer context information (provided through the attention mechanism).
Previous studies on large language models31 and vision transformers32 have shown that performance shows power-law scaling with the amount of training data and the model size. To investigate whether such scaling holds for sEMG decoding, we examined the offline decoding performance of models trained on data from varying numbers of participants (Fig. 2e–g). Across all tasks, we observed reliable performance improvements as a function of the increasing number of participants in the training corpus. Consistent with other domains, empirical performance follows a power law both as a function of parameters and data quantity, with the parameters of the scaling relationship shared across architecture sizes (Methods). The largest models showed promising offline performance.
Online evaluation of generic models
Ultimately, closed-loop performance of our sEMG decoding models is the critical evaluation that confirms their viability as a computer interface. For each task, closed-loop evaluation was performed on naive participants who had not previously had meaningful experience using any sEMG decoder on that task (n = 17 (wrist), n = 24 (discrete gestures) and n = 20 (handwriting)). The core tasks involved using the wrist-angle decoder to continuously control a 1D cursor to acquire targets, the discrete-gesture decoder to navigate and perform actions in a discrete lattice, and the handwriting decoder to write out prompted phrases that were then visualized on the screen (Fig. 3a–c; the evaluation tasks are described in the Methods; see Supplementary Videos 1–3 for representative performance, and Extended Data Fig. 7 for a depiction of the task dynamics). For each task, the participants performed three distinct blocks of trials to allow for characterization of learning (50 trials per block for wrist, 10 trials for discrete gestures and handwriting), with the first block always being a practice block that allowed them to adapt to the controller.
For all of the tasks, we observed learning effects, whereby the participants improved with experience. During the practice block, the supervisor gave verbal coaching—for example, “swipe faster” or “write more continuously”—as needed to improve participant’s performance. The participants were typically able to perform each task on their own after the initial practice block but, for the discrete gestures and handwriting tasks, we found that coaching during the evaluation block was valuable for a subset of participants on trials that they struggled to complete (Methods).
Every participant was able to complete every trial of the three tasks. For wrist control, all of the participants were able to successfully navigate to each target and stay on the target for 500 ms to acquire it. Performance was characterized by time to target acquisition (Fig. 3d) and dial-in time, which measures the time taken to acquire the target after having exited it prematurely (Fig. 3e; definitions are provided in the Methods). We found learning effects in which participants improved in both of these metrics from the practice block to the evaluation blocks, and the majority of them subjectively reported that the cursor moved in the intended direction >80% of the time (Extended Data Fig. 8e).
a–c, Schematics of the three closed-loop tasks. a, Horizontal cursor (wrist): the participants control a cursor (red circle) to acquire a target (green rectangle) in a row of possible targets (grey rectangles). b, Discrete grid navigation: the participants use thumb swipe gestures to navigate, and perform activation gestures prompted by coloured shapes. c, Text entry: the participants handwrite prompted text. (Methods, Extended Data Fig. 7 and Supplementary Videos 1–3). d,e, The performance of n = 17 naive test participants using the wrist decoder in the horizontal cursor task. d, The mean target-acquisition time (excluding the 500 ms hold) in each task block. e, The mean dial-in time in trials in which the cursor prematurely exited the target before completing the hold. Inset: the fraction of trials with premature exits. The dashed red and orange lines in panels e and d show the median task performance with the ground truth wrist angles measured by motion capture (n = 162, with no previous task exposure) and with the native MacBook trackpad (n = 17, with previous task exposure), respectively (Methods). f–h, The performance of n = 24 naive test participants using the discrete-gesture decoder in the grid navigation task. f, The fraction of prompted gestures in each block for which the first detected gesture matches the prompt (first-hit probability). g, The mean gesture completion rate in each task block. The dashed red lines in panels f and g show the median task performance of a different set of n = 23 participants using a gaming controller (Methods). h, Confusion rates (normalized to expected gestures) in evaluation blocks, averaged across participants. Early release denotes a hold of less than 500 ms. i,j, The performance of n = 20 naive test participants using the handwriting decoder on the text entry task. i, The online CER in each block. j, The WPM in each block. The dashed red line shows the median WPM of a different set of n = 75 participants handwriting similar phrases in open loop without a pen (Methods). For each participant, the online CER and WPM are calculated as the median over trials in each block. For all panels, statistical analysis was performed using two-tailed paired sample Wilcoxon signed-rank tests; *P < 0.05, **P < 0.005; not significant (NS), P > 0.05. The boxes show the median (centre line) and lower and upper quartiles (box limits), and the whiskers extend to ±1.5 × interquartile range. The printed numbers show the median and outliers are marked with open circles. For each baseline device, the dashed lines show the median over participants and the shading shows the 95% confidence intervals estimated using the reverse percentile bootstrap with 10,000 resamples.
For discrete gestures, all of the participants were able to complete the task by navigating with the swipe gestures and performing the activation gestures (thumb tap, index pinch and hold, middle pinch and hold) when required. Performance on the discrete-gesture task was characterized by a measure of how often the first detected gesture following a prompt matched the prompted gesture (Fig. 3f) as well as how long it took to complete each prompted gesture (Fig. 3g). The confusion matrix across discrete gestures is shown in Fig. 3h. Note that errors on this task (reflected in both confusions and first-hit probabilities) are a combination of model decoding errors as well as behavioural errors, whereby the participant performed the wrong gesture. This is evident in the fact that confusions were also present when performing this task using a gaming controller rather than an sEMG decoder (Extended Data Fig. 8b–d). Index and middle holds were sometimes released too early (that is, the detected release followed the detected press less than 0.5 s later), and this was indicated in the confusion matrix as an ‘early release’.
The performance of the closed-loop handwriting decoder was evaluated by participants entering prompted phrases and was characterized by the online character error rate (CER; Fig. 3i) and speed of text entry (Fig. 3j). Improvements from practice to evaluation blocks indicate that participants were able to use the practice trials to discover handwriting movements that were effective for writing accurately with the decoder.
For each of these interactions, we also provide performance metrics for a baseline interface that does not rely on decoding sEMG (dashed horizontal lines in each panel). For 1D continuous control, we find that a MacBook trackpad and motion capture ground-truth wrist-based control lead to improved median acquisition times of 0.68 s and 0.96 s, respectively, compared with 1.51 s for the sEMG wrist decoder. For discrete grid navigation, using a Nintendo Joy-Con game controller showed a median gesture completion rate of 1.45 completions per second versus 0.88 with the sEMG discrete-gesture decoder. For prompted text entry, the participants performed open-loop handwriting on a surface, without a pen, at 25.1 WPM, higher than the 20.9 WPM achieved with the sEMG handwriting decoder (and below 36 WPM achievable with mobile phone keyboard33). While our sEMG decoders therefore have room to improve relative to these baseline devices, they are sufficiently performant to reliably complete each task, while not requiring the use of hand-encumbering devices or external instrumentation.
Representations learned by the discrete-gesture model
To develop an intuition about how the generic sEMG decoders function, we visualized the representations learned by the intermediate layers of the discrete-gestures decoder. The network architecture consisted of a 1D convolutional layer, followed by three recurrent LSTM layers (Fig. 4a) and, finally, a classification layer.
a, Schematic of network architecture. Conv1d denotes a 1D convolutional layer. The final linear readout and intermediate normalization layers are not shown (Methods). b, Representative convolutional filter weights (16 input channels × 21 timesteps) from the first layer of the trained model. c, Example heat maps of the normalized voltage across all 16 channels for putative MUAPs recorded with the sEMG wristband (Methods and Extended Data Fig. 2) after high-pass filtering (Methods). d,e, The frequency response of the channel with maximum power (d) and the root mean square (RMS) power per channel (e), both normalized to their respective peaks, for each example convolutional filter (blue lines) and putative MUAP (orange lines) from b and c, respectively (see also Extended Data Fig. 9). For comparison, the dashed black lines show these curves calculated over an entire recording session, averaged over ten randomly sampled sessions from the model training set. For d, we used the mean temporal frequency response over all 16 sEMG-RD channels. The sharp frequency response cut off at 40 Hz is from high-pass filtering (Methods). f–h, Principal component analysis projection of LSTM representations of 500 ms sEMG snippets aligned with instances of each discrete gesture, from three participants held out from the training set, each with three different band placements. Each row shows the representation of each LSTM layer. Each column shows the same data, coloured by discrete gesture category (f), participant identity and band placement (g) or sEMG RMS power (h) at the time of the gesture. i, The proportion of total variance accounted for by each variable, for each layer (n = 50 test participants; Methods). Statistical analysis was performed using two-tailed paired sample t-tests; ***P < 0.001. The error bars (barely visible) show the 95% Student’s t confidence interval for the mean.
To interpret the convolution layer, we visualized representative spatiotemporal filters (Fig. 4b) alongside putative MUAPs (Fig. 4c) detected using the wristband during low-movement conditions (Extended Data Fig. 2). The filters appear to form a coarse basis set spanning the statistics of MUAPs; specifically, Fig. 4d,e shows the general similarity in temporal frequency content and spatial envelope between the putative MUAPs and emergent convolutional filters (Extended Data Fig. 9).
To examine the intermediate LSTM representations, we visualized the changing representational geometry across layers. We analysed the representations of four properties: gesture category, participant identity, band placement and gesture-evoked sEMG power (a proxy for behavioural variability over executions of the same gesture). Figure 4f–h shows LSTM hidden-unit activity at each layer evoked by snippets of sEMG activity triggered on discrete-gesture events, coloured by one of the four aforementioned properties. By examining the dominant principal components (PCs), we observed a trend of gesture category becoming more separable deeper in the network as the representations of each gesture become more tightly clustered and less or equally sensitive to nuisance variables (participant identity, band placement and power). With increasing depth in the network, gesture category accounted for an increasing proportion of the variance in the representation of each layer (Fig. 4i and Methods). In summary, the network learns to solve this task by progressively shaping its representation of the sEMG to be more and more invariant to nuisance variables.
Personalizing handwriting models improves performance
While generic models allow a neuromotor interface to be used with little to no setup, performance can be improved for a particular individual by personalizing the generic model to data from that participant. Personalization has shown benefits to accuracy for related problems in automatic speech recognition in language models34 and acoustic models35 as well as speech enhancement36. We explored personalization for the handwriting task through the fine-tuning of all of the generic model’s parameters using additional supervised data from a set of 40 held-out participants not included in the training data of the generic model. For each participant, we held out three sessions of data (Methods) and then trained personalized models for 300 epochs without early stopping on varying amounts of data from their remaining sessions (Fig. 5a).
a, Schematic of the supervised handwriting decoder personalization. Predictions before and after personalization are shown above and below example prompts (such as ‘howdy!’) for two participants (left and right). The green and purple font denotes correct and incorrect character predictions, respectively. b, The mean performance (n = 40 test participants) of models pretrained on varying numbers of participants (red line) and fine-tuned on varying amounts of personalization data for each test participant (shades of blue). The dashed lines show power law fits (Methods). c, The relative reduction in offline CER that personalization provides beyond a given generic model, for varying amounts of pretraining participants and personalization data. The dashed lines show the relative improvements calculated from the power law fits in b. d, The relative increase in the number of pretraining participants that matches CER reduction from fine-tuning on varying amounts of personalization data (Methods), for generic models with varying amounts of pretraining participants. A value of 1 indicates doubling the number of pretraining participants. The dashed lines show the relative increases calculated from the power law fits in b. e, The relative reduction in offline CER (beyond the 60.2-million-parameter 6,527-participant pretrained generic model) achieved for each test participant (rows) by personalizing on 20 min of data from every other test participant (columns), sorted by the diagonal values. f, The relative reduction in CER achieved for each test participant (n = 40) by fine-tuning on 20 min of personalization data, as a function of the pretrained generic model CER for that test participant (60.2-million-parameter model), across various numbers of pretraining participants. Improvements from personalization are correlated with the CER of the pretrained generic model. We show the range of Pearson correlation coefficients across numbers of pretraining participants and the median P value (two-sided test); the maximum P value over all fits is 0.0035.
Fine-tuning generic models improved their average offline CER for all amounts of additional data and for all numbers of pretraining participants (Fig. 5b). Even for generic models trained on 6,400 participants, using just 20 min of personalization data resulted in a 16% improvement in the median performance (Fig. 5c). In all cases, more personalization data led to further reductions in the average per-user CER across the personalized participants. However, across all generic models, as the generic model was pretrained with data from more participants, the absolute and relative improvement in CER from personalization decreased (Fig. 5c), indicating that there are diminishing returns to personalizing already performant generic models.
Personalizing models is therefore an alternative to expanding the generic corpus size to decrease a model’s CER on the target participant (Fig. 5d). For example, for the model pretrained on the smallest corpus of 25 participants (or 1,900 min), personalization with 20 min of data from the target participant was equivalent to training a generic model with 14,000 min of additional data from other participants—7× as much data as in the original pretraining corpus. However, as more data from other participants are added, the effective enhancement of the generic training corpus achieved through personalization diminishes. Adding 14,000 min of pretraining data is equivalent to 20 min of personalization data for the 25 participant model and only about 1 min for the 200 participant model.
While personalization improved performance on the target participant, model performance improvements from personalization caused the model to overfit to the target participant and did not transfer across participants. For the most performant generic model trained (6,527 participants, 60.2 million parameters), personalizing on one participant and evaluating on another participant generally had a negative impact on performance when compared to the generic model performance (Fig. 5e). Personalization on the same participant improved the performance in 88% of the participants and led to a relative improvement of 8.35 ± 2.36% (median ± s.e.m. over participants), whereas data from one participant used to personalize another participant improved performance on only 7% of such participant pairs and led to an average relative decrease of 8.86 ± 0.53% (median ± s.e.m., taken across each evaluation participant after averaging across personalized models; Methods).
Personalization disproportionately improved the performance of poorly performing participants across all generic models (Fig. 5f). For example, for generic models pretrained with 6,527 participants, personalization provided larger relative gains for participants with higher generic model CER (Fig. 5f) and more moderate gains or occasional regressions for those with already low CERs. In Extended Data Fig. 10, we show that these regressions can be mitigated with early stopping during fine-tuning, albeit at the cost of increased data required for validation.
Overall, these results highlight clear trends and trade-offs for personalization, facilitating the rational design of data collection. We expect that personalization will provide a practical solution for enhancing the average per-user performance when further scaling generic data collection to achieve a target performance level is prohibitive. Moreover, personalization can effectively address the long tail of users experiencing poor performance with the generic model, as it ensures considerable relative performance improvements for these users.
Discussion
Here, we introduce an easily donned/doffed wrist-based neuromotor interface capable of enabling a diverse range of computer interactions for novel users. We developed a scalable data-collection framework and collected a large training corpora across diverse participants (Fig. 1). We used supervised deep learning to produce generic sEMG models (Fig. 2) that overcome issues that have long stymied generalization in BCIs and sEMG systems. The resulting sEMG decoders enabled continuous control, discrete input and text entry in closed-loop evaluations without the need for session- or participant-specific data or calibration (Fig. 3). A dissection of intermediate representations in the discrete-gesture neural-network decoder highlighted its ability to disentangle nuisance parameters related to band placement and behavioural style (Fig. 4). Finally, we demonstrated improvements to handwriting decoding performance with additional personalization data (Fig. 5). Together, this work defines a framework for building generic interaction models using non-invasive biological signals.
Related work in HCI and BCI
The work presented here sits at the nexus between HCI and BCI. The HCI community has placed significant emphasis on advancing gestural input for various technology applications by deploying machine-learning-backed solutions for differing sensing modalities such as computer vision (for example, Kinect, Meta Quest) inertial measurement units37,38, sEMG24,39,40, bio-acoustic signals41, electrical impedance tomography42, electromagnetic signals43 and ultrasonic beamforming44. The most direct antecedent of our work uses the discontinued commercial sEMG Myo armband (worn on the forearm) for gesture detection, and wrist movement39, in datasets with more than 600 participants45,46. However, to date, sEMG-based approaches have typically been offline or necessitated within-session or participant-specific calibration, limiting their real-world use47.
Our non-invasive sEMG work has intimate connections to BCI. EEG-based BCI systems (notably, spellers) can achieve impressive bitrates of 100–300 bits per minute48 (versus 528 bits per minute for our handwriting decoder). However, EEG performance generally lags behind other BCI modalities due to issues with signal quality, interpretation and lack of standardized hardware or software49. As a result, efforts have been focused on small models and relatively small datasets (for example, <50 users50).
Intracortical BCI offers higher signal-to-noise ratio, but has been limited to single-participant studies due to nonstationarities in recordings and over sessions5,11,12,29. While the field of BCI is transitioning to neural network decoders4,29,51,52, it remains focused on solving these calibration issues, which are largely a function of limited data. Given that sEMG signals derive from the summed activity of motor unit firing, it is possible that sEMG-decoding methods such as those described here can guide methods development for intracortical BCI systems. The large-scale approaches demonstrated here may provide direction to the larger BCI field, such as BrainGate2,4 or Neuralink53.
Comparison to HCI baselines
To contextualize the absolute performance of our sEMG decoders, we compared their performance to both common input methods and those using similar gestures as our sEMG decoders use: a MacBook trackpad and motion capture ground truth wrist angles for 1D continuous control, a Joy-Con game controller for discrete grid navigation and open-loop prompted handwriting for text entry. In each case, these baseline devices outperform our sEMG decoders.
However, we note that these baseline interfaces cannot fulfil the same role as an always-available sEMG wristband, as they require cumbersome equipment: tracking wrist angles requires multiple calibrated cameras, using a laptop trackpad or a gaming controller encumbers the hand, and handwriting requires a pen, paper and a surface. For tasks in which constant availability is important (such as on-the-go scenarios), the reductions in current decoder performance may therefore be acceptable.
Regardless, we expect further improvements in sEMG decoding through continued development of user familiarity/skill over time, improved models (including through personalization), post-processing and hardware innovations for superior sensing. We also note that the gestures used with our sEMG decoders are novel, and we found that coaching typically improved sEMG decoder performance (Methods). We expect user proficiency to grow with increased familiarity with the sEMG-RD and underlying gestures.
Future directions
Our sEMG decoder enables direct intentional motor signal detection from the muscle, thereby opening directions in novel and accessible computer interactions. For example, such a decoder could be used to directly detect an intended gesture’s force, which is generally unobservable with existing camera or joystick controls. While we demonstrated accurate, fully continuous control over only one degree of freedom, it is also likely that joint control of multiple degrees of freedom is achievable through additional, separate biomimetic mappings such as adding ulnar/radial deviation of the wrist for vertical control. Moreover, the sensitivity of sEMG to detect signals as subtle as putative individual MUAPs (Fig. 1b and Extended Data Fig. 2) enables the creation of extremely low-effort controls—an important innovation with a potential impact for people with a diverse range of motor abilities or ergonomic requirements54. Explorations of interactions in neuromotor signal space—as opposed to gesture space—may enable entirely new forms of control, for example, by exploring the limits of novel muscle synergies or interaction schemes that directly depend on individual motor unit recruitment or firing-rate control.
As a research platform, the sEMG-RD and associated software tooling could enable study of the effects of neurofeedback on motor unit activity for novel human–machine interactions55,56, the learning of novel motor skills57 or the limits and mechanisms of motor unit control58.
Finally, in the clinic, the ability to design interactions that require only minimal muscular activity, rather than performance of a specific movement, could enable viable interaction schemes for those with reduced mobility, muscle weakness or missing effectors entirely59, as well as the development of effective closed-loop neurorehabilitation paradigms60. It is unclear whether the generalized models developed here and trained on able-bodied participants will be able to generalize to clinical populations, although early work appears promising54. Personalization can be applied selectively to users for whom the generic model works insufficiently well due to differences in anatomy, physiology or behaviour. However, all of these new applications will be facilitated by continued improvements in the sensing performance of future sEMG devices, increasingly diverse datasets covering populations with motor disabilities, and potentially combining with other signals recorded at the wrist, such as IMU or biosignals.
Methods
Hardware
sEMG-RD
The sEMG devices consisted of two primary subcomponents: a digital compute capsule and an analogue wristband (Extended Data Fig. 1). The digital compute capsule comprised the battery, antenna for Bluetooth communication and a printed circuit board that contained a microcontroller, an analogue-to-digital converter and an inertial measurement unit. The analogue wristband comprised discrete links that each housed a multilayer rigid printed circuit board that contained the low-noise analogue front-end circuits and gold-plated electrodes. We manufactured the sEMG-RD device in four sizes. The analogue front end applied 20-Hz high-pass and 850-Hz low-pass filters to the data.
These printed circuit boards were inserted into Nylon 12 PA 3D printed housings and then strung together with a multilayer flexible printed circuit board along with a strain-relieving fabric. An elastic nylon cord was routed continuously between the links and was tied together at the wristband gap to form a clasp and tensioning mechanism. Finally, the digital compute capsule was connected to the analogue wristband through a connector on the flexible printed circuit board and fastened together with screws for mechanical stability. The device underwent a biocompatibility testing process to ensure its safety. The band is easily donned at the wrist with the only requirements being that the compute capsule is on the dorsal side and the gap is near the ulna bone.
Data collection
MRI scan
To visualize the position of the sEMG-RD’s electrodes relative to wrist anatomy, we collected a high-resolution anatomical MRI scan (Siemens Magnetom Verio 3T) from a consenting participant’s right forearm. We collected axial scans along the forearm, beginning from just distal to the wrist and ending just distal to the elbow. The scan was collected pursuant to an IRB governed study protocol conducted by Imperial College London.
Participant experience
All data collection was done at either Meta’s internal data-collection facilities or at third-party vendor sites. Study recruitment and participant onboarding was performed according to protocol(s) approved by an external IRB (Advarra). All studies began by providing the participants with information about the study protocol and asking them to review and sign an IRB-reviewed consent form before beginning the study. The participants were provided with the opportunity to ask questions before their participation and were able to discontinue their participation at any time. On-site research administrators monitored participants during the study protocol(s) to ensure participant well-being. The participants were financially compensated for their time participating in the study.
Collection at scale
The participants visited data-collection and laboratory facilities to perform the study protocols. On a given day, there were up to 300 participants who partook in a study. Once a participant was in the facility, measurements of the wrist and hand were taken, including the forearm circumference and wrist circumference. Next, we fitted them with an appropriately sized band to collect sEMG data; small, 130–148 mm; medium, 148–169 mm; large, 169–193 mm; and extra large, 193–220 mm.
All of the participants received general coaching in the form of a study introduction, in-person demonstration of the correct and incorrect movements, and general supervision of participant compliance by research assistants. Study sessions lasted around 2–3 h (including rests and briefing). All responses and information provided during the study were collected and stored using de-identification technique(s) in a secure database.
While all collection occurred in controlled environments, training and testing datasets demonstrated large variance along band placement, sweating, skin condition, demographic diversity, local climate and other axes.
Prompted study design
All of our tasks were framed as supervised machine learning problems. For the handwriting and discrete-gesture recognition tasks, we relied on prompting to obtain approximate ground truth for our data, rather than direct instrumentation using physical sensors. While prompt labels depend on participant compliance, we found that instrumentation imposed constraints on what could be explored, as dedicated sensors need to be built for each individual modelling task. Furthermore, the use of sensors such as gloves or pressure sensitive pads limited the ecological validity of the signal, as physical sensors can restrict the movement range, poses and conditions examined.
For the wrist task, we used motion capture to continuously track the participant’s wrist angle (see below). In this case, we used a mixture of open-loop prompting (as for the discrete-gesture and handwriting tasks) and closed-loop interactions, in which participants performed cursor control tasks in which the cursor’s position was determined from their wrist angles tracked in real time (see below).
Training and evaluation protocols were implemented in a custom, internal software framework that took advantage of the abilities of Lab.js, an established open-source web-based study builder61. This framework orchestrated both the presentation of task-specific prompter applications and the recording of annotations from these applications. The framework was developed using TypeScript and the task-specific prompters were built on the React framework.
We created the overview figure of our data-collection approach in Fig. 1a using a photograph taken at our data-collection facility as a reference, which was then traced and edited in Procreate, with additional colour and graphical elements added in Adobe Photoshop.
Real-time data-collection system
Data collection for our studies was performed using an internal framework for real-time data processing that supports data collection, offline model training, and benchmarking and online evaluation. At its core, the framework offers an engine for defining and scheduling a data-processing graph. On the periphery, it provides well-defined APIs for real-time performance monitoring and interaction with consumer applications (for example, prompting software, applications for stream visualization).
For data collection, our internal platform served as the host for recording real-time signals and annotations to a standardized data format (that is, HDF5). For offline model training and benchmarking, our internal platform provides an API for batch processing of data corpora. This helps to generate featurized data from the recorded raw-signals and apply model inference for offline evaluation. To ensure online and offline parity, the internal platform also supports running the same sequence of processing steps on real-time signals for online evaluation.
Offline training data corpora
Wrist corpus
The wrist decoder training corpus included simultaneous recordings of sEMG and ground truth flexion-extension wrist angle (measured with motion capture) from 162 participants, 96 of whom recorded 2 sessions (both sessions from each of these participants were included in the same train or test split to which they were assigned). To track flexion-extension and ulnar-radial deviation wrist angles, we placed two light (16 g) 3D printed rigid bodies on the back of the hand and on the digital compute capsule of the sEMG-RD. Each of these rigid bodies had three retroreflective markers attached, which together defined a 3D plane that was tracked in 3D in real time (60 Hz) with <1 mm resolution using 18–30 PrimeX 13 W cameras (OptiTrack). We used the relative orientation of these two planes to calculate the flexion-extension and ulnar-radial deviation wrist angles. Only the flexion-extension angle was used for training and evaluating wrist decoders.
Each session consisted of an open-loop stage, a calibration stage and a closed-loop stage, in which the participants controlled a cursor that determined its position from these two wrist angles. Throughout all stages, the participants were instructed to keep their hand in a ‘laser pointer’ posture, with a loose fist in front of the body, thumb on top and elbow at approximately 90°.
In the open-loop stage, the participants performed centre-out wrist deflections in eight possible directions (four cardinal directions and four intercardinal directions) following a visual prompt (Extended Data Fig. 4a), for a total of 40 repetitions (5 per direction) in a pseudorandomized order.
In the closed-loop stage, the participants were asked to perform two tasks to the best of their abilities: a cursor-to-target task and a smooth pursuit task. In both tasks, the flexion-extension and radial-ulnar deviation wrist angles were normalized by their range of motion (measured in a calibration stage), centred by the neutral position (measured by prompting the user to hold a neutral wrist angle), and then respectively mapped to the horizontal and vertical position of a cursor on the screen, in real-time (60 Hz). This mapping consisted of simply scaling the (normalized and centred) wrist angles by a constant gain, gx. To encourage both small and large wrist movements, two different gains were used: gx = 2.0 pixels per normalized radian (half of range of motion) and gx = 4.0 pixels per normalized radian (quarter of range of motion). Gains larger than 1.0 were required for every user to be able to reach the corners of the workspace.
In the cursor-to-target task, the participants were prompted to move the cursor to one of the equally sized rectangular targets presented on the screen. During each trial, one of the targets was highlighted, and the participant was instructed to move the cursor towards that target. The target was acquired when the cursor remained within the target for 500 ms. Once a target was acquired, the rectangular target disappeared, and one of the remaining targets was prompted, initiating the next trial, in a random sequence. Once all of the targets were acquired, a new set of targets was presented. Three different target configurations were used: horizontal (10 targets presented side-by-side along the horizontal axis, with the cursor confined to this axis; Extended Data Fig. 7a), vertical (10 targets presented one on top of the other along the vertical axis, with the cursor confined to this axis) and 2D (25 targets presented in a 5 × 5 square grid; Extended Data Fig. 4b). These three configurations were presented in this order in a block structure. In the horizontal target configuration block, the participants had to acquire all 10 horizontal targets, and repeat this 10 times, for a total of 100 trials. The first 5 repetitions (50 trials) were performed with the lower cursor gain and the last 5 repetitions (50 trials) were performed with the higher cursor gain. The vertical target configuration block followed the same structure, and the 2D target configuration block consisted of 4 repetitions (for a total of 100 trials), with the first 2 performed with the lower cursor gain and the last 2 with the higher cursor gain.
Finally, in the smooth pursuit task, the participants were instructed to move the cursor to follow a moving target on the screen as closely as possible (Extended Data Fig. 4c). Each trial consisted of a 1-min random target trajectory, generated by taking a random combination of 0.1 Hz to 0.25 Hz sinusoids (with randomly sampled phases) along the horizontal and vertical axes. The participants performed a total of four trials, the first two of which were performed with the lower cursor gain and the last two with the higher cursor gain.
Only data within these task stages (open-loop, cursor-to-target and smooth pursuit) were used for model training and offline evaluation. All data outside of these stages were excluded from the model training and test sets. We also excluded data from the cursor-to-target task with the vertical target configuration, as the flexion-extension wrist angle was mostly constant during this task.
Discrete-gesture corpus
The discrete-gesture training corpus was composed of data from 4,900 participants. As noted in the main text, there were nine prompted gestures: index and middle finger presses and releases, thumb tap and thumb left/right/up/down swipes. Each session consisted of stages in which combinations of gestures were prompted at specific times (Extended Data Fig. 4d,e). These combinations usually included the full set of trained gestures but, in some stages, were restricted to specific subsets (for example, pinches only, thumb swipes only). During data collection for these stages, the participants were asked to hold their hand and arm in one of a range of postures (hand in front, palm facing in/out/up, hand in lap, arm hanging by side, forearm pronated inwards) or to translate/rotate their arms while completing gestures. In around 10% of stages, instead of prompting specific timing, the participants were asked to complete sequences of 3–5 gestures at their own pace. About one-third of the training corpus was composed of a range of null data in which participants were either asked to generate specifically timed null gestures (such as snaps, flicks) or to engage in more loosely prompted longer-form null behaviours (such as typing on a keyboard). On average, gestures occur in around 6% of samples. The gestures were unevenly distributed, with thumb gestures being more frequent. Given that an event has occurred, individual gesture probabilities range from around 9% to 13%. When considering the entire dataset including null cases, the probability of correctly guessing any specific gesture falls below 1%.
Handwriting corpus
The handwriting recognition corpus comprised sEMG recordings from a total of 6,627 participants. The data were collected in short blocks, during which the participants were prompted to write a series of randomly selected items, including letters, numbers, words, random alphanumeric strings or phrases (Extended Data Fig. 4f,g). The participants were prompted with spaces inserted both implicitly and explicitly between words. In implicit space prompting, the participants advance from one word to the next naturally as with pen and paper writing. In explicit space prompting, prompts with a right dash character would be presented after each word, instructing the participants to perform a right swipe with their index finger that would later be remapped to a space. This can constrain the modelling problem, avoiding the need for the model to infer spaces implicitly by relying on factors such as the linguistic context of the text being written. We sampled phrases from a dump of Simple English Wikipedia in June of 2017, the Google Schema-guided Dialogue Dataset62 and the Reddit corpus from ConvoKit63, after filtering to remove offensive words and phrases. Each participant contributed varying amounts of data, but approximately 1 h and 15 min each on average. Each block was performed in one of three randomly chosen postures: seated writing on a surface, seated writing on their leg as the surface or standing writing on their leg. Note that we did not have ground truth information about the fidelity with which participants wrote these prompts but, for a subset of participants, handwriting was performed with a Sensel Morph touch surface device. Visual examinations of a subset of the Sensel recordings suggested that approximately 98% of prompted characters were executed successfully.
sEMG preprocessing
Putative motor unit action potential waveform estimation
Figure 1b shows the spatiotemporal waveforms of MUAPs evoked by subtle contractions of the thumb and pinky extensors in one participant. For each digit, the participant selected the sEMG channel with maximum variance during sustained contractions based on visual inspection of the raw signals. Down-selecting to one channel enabled greater acuity for visual biofeedback during data collection. Subsequently, the participant was prompted to alternate between resting and performing sustained contractions of the chosen digit for three repetitions while receiving visual feedback about the raw sEMG signal on the selected channel. Each rest and movement prompt was 10 s long with 1 s interprompt intervals. The participant used the visual feedback on the selected channel to titrate the amount of generated force to recruit as few motor units as possible with each contraction64,65.
We estimated the MUAP spatiotemporal waveforms W (W ∈ \({\mathbb{R}}\)L×C, where L is the number of samples (40) and C is the number of channels (16)) for each digit using a simple offline spike-detection algorithm. The sEMG traces were first preprocessed by filtering with a second-order Savitzky–Golay differentiator filter with a width of 2.5 ms (5 samples). The filtered sEMG was rectified to improve the alignment of detected MUAPs, averaged over channels, then smoothed with a 2.5 ms Gaussian filter to obtain a 1D sEMG envelope. Spikes were detected by peak finding on the sEMG envelope using scipy.signal.find_peaks with prominence=0.5 (ref. 66). MUAPs were extracted using a 20-ms-long window across all sEMG channels, centred on each peak. The waveforms shown in Fig. 1b were obtained from the selected channel for thumb extension (12; blue) and pinky extension (14; pink) using all MUAPs detected during the second prompted movement period; no attempt was made to cluster MUAPs into different units. For visualization, the opacity of each trace was scaled as 1/(1 + |ai − median(a)|), where ai is the peak-to-peak amplitude of the ith MUAP and a is the amplitudes of all detected MUAPs for each contraction.
MPF features
The wrist and handwriting generic sEMG decoders used custom features extracted from the raw sEMG; we refer to this feature set as MPF features. To obtain these features, we first rescaled the sEMG by 2.46 × 10−6, to normalize the s.d. of the noise to 1.0 (this value was determined empirically). Motivated by the need to remove motion artifacts67, we then applied a 40 Hz high-pass filter (fourth-order Butterworth) to the sEMG recordings sampled at 2 kHz. We then extracted the squared magnitude of the cross-spectral density with a rolling window of T sEMG samples and a stride of 40 samples (20 ms). We used T = 200 samples (100 ms) for the wrist decoder and T = 160 samples (80 ms) for the handwriting decoder. The cross-spectral density was chosen to preserve cross-channel relationships in the spectral domain. We estimated the magnitude of cross-spectral density by first taking the outer product (over channels) of the discrete Fourier transform of the signal (64 sample (32 ms), stride of 10) with its complex conjugate. We then binned the result into 6 frequency bins (0–62.5, 62.5–125, 125–250, 250–375, 375–687.5, 687.5–1,000 Hz). We summed this product over each frequency bin, and took the square of the absolute value of the sum over frequencies. This produced a set of 6 symmetric and positive definite 16 × 16 square matrices that update every 40 samples, for an output frequency of 50 Hz. Building on robust results in the EEG space for this class of features, we applied a log-matrix operation on each of these matrices68. Finally, the diagonal and the first three off-diagonals (rolled over the matrix edge to account for the band being circular) were preserved and half-vectorized for each matrix, and then concatenated across the 6 frequency bins, producing a single 384 (6 × 4 × 16) dimensional vector for each 80 ms window. An implementation for both the cross spectral density estimation and taking the matrix logarithm can be found in the pyRiemann Python toolbox69.
Discrete-gesture time alignment
As all discrete-gesture data collection was performed by prompting participants, we had access to only approximate timing of the gesture execution (that is, the time at which the participant was prompted to perform the gesture). However, training sEMG decoding models to infer when the participant performs a gesture required more precise alignment of labels with the signal to be effective. While a task like handwriting used an alignment free loss (that is, connectionist temporal classification, CTC) and would be applicable in this task as well, forced-alignment enabled us to gain much finer control over the latency of the detections produced by our models, which was critical for practical use of discrete gestures as control inputs.
When gestures were well isolated, that is, when the intergesture interval was greater than the uncertainty of the timing, existing solutions from the literature could be readily deployed on sEMG data, leading to robust inference of gesture timing70. However, realistic data collection involved rapid sequence of gestures in close succession, which made identification of timing of individual gestures a challenging problem and required a dedicated solution. We therefore developed an approach to infer the precise timing of the gestures.
Our approach was to infer the timing of all gestures in a sequence, defined as a series of consecutive gestures for which uncertainty bounds overlap. We did this by searching for the sequence of gesture timings that best explained the observed data according to a generative model of our MPF features.
First, for the purposes of this timing adjustment stage, we defined the generative model for a set of K gesture instances as the sum of gesture-specific templates centred at corresponding event times, tk, with additive noise:
$$x(t)={\sum }_{k=0}^{K}{\phi }_{k}(t-{t}_{k})+n(t)$$
where x(t) is our features over time, ϕk(t) is a prototypical spatiotemporal waveform for gesture of index k (that is, the gesture template for the class of gesture corresponding to event k) and n(t) is a noise term. We note that this generative model is only valid for ballistic gesture execution and power-based features. We also note that templates are shared across executions of the same gesture type, but specific to each participant and band placement.
We define the generative inference as the joint optimization of gesture templates and times at which each gesture occurred. For each recording, we solved this through an iterative algorithm: we first estimated the templates based on prompted times, then inferred timestamps of the gesture sequence, and repeated with new inferred event times until convergence (that is, when the timestamp updates across iterations of the EM algorithm were smaller than a tolerance value).
Templates were estimated by an EMG analogue of the regression-based estimator of the event-related potential (rERP), to disentangle overlapping contributions of gestures performed in a fast sequence71. Timings were obtained by the following optimization problem:
$${\min }_{{t}_{k}={\rm{0..}}.K}{\int }_{t}{(x(t)-{\sum }_{k=0}^{K}{\phi }_{k}(t-{t}_{k}))}^{2}{\rm{d}}t$$
We optimized this numerically through a beam search algorithm, subject to additional ad hoc constraints that bounded how far the adjusted times could deviate from the prompted times based on priors from the data-collection protocol.
Direct application of the above procedure produced timestamps that were referenced to the session template, and there was an indeterminacy as to the timing offset within the gesture, which can vary due to initial conditions. To better standardize alignment of template timing across individuals, we performed a global recentring step at the end of timestamp estimation. Specifically, we found the time of maximal correlation between the session template (that is, for a particular participant) and a global template (grand average of all templates across participants).
Gesture-trigged sEMG activations
To inspect the structure of sEMG activations across gestures and participants (Fig. 2b), we used EMG covariance features. Specifically, we concatenated the 0-, 1- and 2-diagonals of the sEMG covariance matrix over a 300 ms window centred on each gesture, yielding a 48 × 60-dimensional feature space. To produce the embeddings, we ran t-SNE in two dimensions with perplexity 35 on the flattened feature space.
Single-participant discrete-gesture modelling
Training details
To train the single-participant models for the discrete-gesture classification task, we selected 100 participants who had completed at least five sessions of data collection and selected five of those sessions. We then randomly picked four of these sessions for training and the remaining held-out session for testing. From these four sessions we randomly created nested subsets of two, three and all four sessions to train three different models for each participant. Given the limited amount of training data per model, we used the MPF features and a small neural network as described below.
Architecture
The single-participant discrete-gesture model took as input the MPF features. The network architecture consisted of (a) one fully-connected (FC) layer with Leaky ReLU activation function followed by (b) cascaded time-depth separable (TDS) blocks72 across time scales and (c) three more FC layers to produce a logit value for each of the nine discrete gestures to be predicted. For (b), we used two TDS blocks per time-scale: at each scale s, an AveragePool layer with kernel size 2s was applied to the output of (a) and fed to a TDS block with dilation 2s. The output was then added to the output of scale s − 1 (if it existed) and passed through another TDS block with dilation 2s as the output of scale s to be used by the next scale s + 1 (if it exists) or subsequent layers. We used 6 scales (s = 0, …, 5), and the feature dimension was set to 256 for all TDS blocks and all but the very last FC layer.
Optimization
We used the standard Adam optimizer with the following learning rate schedule: the learning rate increased linearly from 0 to 1 × 10−3 over a five-epoch warm-up phase, then underwent a one-time decay to 5 × 10−4 after epoch 25, and remained constant thereafter. Each model was trained for 300 epochs to avoid under- or over-fitting for single-user models, based on previous empirical observations. A binary cross-entropy loss was used as with the generic model.
Offline evaluation
To evaluate the performance of each model on the given held-out sessions, we followed the same procedure described under the ‘Discrete gestures’ part of the ‘Generic sEMG decoder modelling’ section. In brief, we triggered gesture detections on the corresponding model probability crossing a threshold of 0.35, filtered all detected gestures through debouncing and state machine filtering, and then used the Needleman–Wunsch algorithm to match each ground-truth label with a corresponding model prediction. We then quantified performance using the FNR, defined as the proportion of ground-truth labels for which either the matched model prediction is incorrect or there is no matched model prediction. We calculated the FNR independently for each gesture and then took the average over the nine gestures. We used FNR rather than CLER (the metric used for generic models) owing to the very small number of events detected for some poorly performing models, which lead to a large number of labels without a matched model prediction, which are ignored by the CLER metric.
Generic sEMG decoder modelling
Related deep learning architectures and approaches
The three HCI tasks described here—continuous wrist angle prediction, discrete action recognition and the transcription of handwriting into characters—represent related but distinct time-series modelling and recognition tasks. Machine learning and, specifically, deep learning approaches have become extremely popular solutions to these problems, including convolutional models73, recurrent neural networks74 and streaming transformers30.
As an example of the similarity between our tasks and established machine learning problems, consider the relationship between handwriting recognition from sEMG and automatic speech recognition (ASR) from audio waveforms. Both tasks map continuous waveform signals (with dimensionality equal to the number of microphones or sEMG channels) at a fixed sample rate, to a sequence of tokens (phonemes or words for ASR, characters for our sEMG-RD). Components of our modelling pipeline have analogues in ASR, including feature extraction, data augmentation, model architecture, loss function, decoding and language modelling. As noted below, each of these modelling pipeline components required substantial domain-specific modification for sEMG models.
For feature extraction, ASR typically uses log mel filterbanks; we used our analogous MPF features (see the section ‘MPF features’), as discussed below. For data augmentation, we used the ASR technique of SpecAugment75, which applies time- and frequency-aligned masks to these spectral features during training. A popular model architecture for ASR is the Conformer30, which provides the advantages of attention-based processing in a form that is compatible with causal time-series modelling. We found that this method worked well for sEMG-based handwriting recognition as well. A popular loss function for ASR is CTC76, which allows neural networks to be trained from waveforms and their textual transcriptions, without the need for a precise temporal alignment. As we similarly had pairs of sEMG recordings and transcriptions without precise temporal alignment, we also used CTC to train our models. When decoding models at test time, ASR typically uses a beam search77 to approximate the full forward-backward algorithm lattice78 while still incorporating predictions from a language model, biasing decoding towards more likely character and word sequences. Experimentation presented in this work used ‘greedy’ CTC decoding, although beam decoding with language modelling in our decoders would have been possible79.
In addition to ASR, we drew from an established literature of machine learning approaches for EEG and EMG analysis that explores different signal featurizations and both classical and deep learning architectures. In the case of EMG, more expressive raw sEMG or time-frequency decomposed features (for example, Fourier or Wavelet features) have been shown to achieve stronger performance than coarser temporal statistics like RMS power80,81. In the case of EEG, MPF features68 have proven to be a simple and robust featurization achieving state of the art, or near state of the art, performance for many tasks10. In agreement with the literature, we find that MPF features offer clear advantages on the wrist classification task over RMS power (Extended Data Fig. 6). As MPF features are computed across a sliding window of 100 ms, which is comparable to the temporal extent of our discrete gestures, we chose to instead use raw EMG features for the discrete-gestures task.
Both EMG interfaces and BCIs have been approached with a variety of different learning architectures in the literature, including both classical machine learning approaches (for example, random forest, support vector machine) and deep-learning-based approaches81. While the choice of modelling approach is problem dependent, in general, for large datasets, deep learning approaches outperform more classical machine learning techniques82.
Wrist
To train wrist decoders, we trained a neural network to predict instantaneous flexion-extension wrist angle velocities measured by motion capture (see the ‘Wrist corpus’ section above). We consistently held out a fixed set of 10 participants for validation and 22 participants for testing, and varied the number of training participants from 20 to 130.
Architecture
The wrist decoder network architecture took as input our custom MPF features of the sEMG signal. These features were passed through a rotational-invariance module, which comprised a fully connected layer with 512 hidden units and LeakyReLU activation. This module was applied to sEMG channels that were discretely rotated by +1, 0 and −1 channels, and the resulting outputs were then averaged over the rotation process. This output was then passed through two LSTM layers of 512 hidden units each, a LeakyReLU activation, and a final linear layer producing a 1D output. For the smaller network architecture reported in Fig. 2e, we used only 16 hidden units in the initial MLP and LSTM, and only 1 rather than 2 LSTM layers. A forward pass of the larger architecture required 1.2 million floating point operations (FLOPs) per output sample.
Optimization
We trained each network with the Adam optimizer for a maximum of 300 epochs, with a learning rate of 1 × 10−3. We used an L1 loss function and a batch size of 1,024, with each sample in the batch consisting of 4 (contiguous) seconds of recordings. We evaluated the test performance of the training checkpoint with the lowest L1 loss of the validation data. Training the largest model on the largest training set took 36 s per epoch, for a total of 3 h on a single NVIDIA A10G Tensor Core GPU.
Discrete gestures
To train discrete-gesture models, we segmented training data from participants into groups of 40, 80, 160, 320, 640, 1,280, 2,800 and 4,800 participants. For each group, we tested the generalization performance of models on offline data from the same set of 100 held-out participants. For validation, another set of held-out users was used; we used a random set of 16 users for the training groups of size 40 and 80. For larger groups, 10% of the training users were used for validation. Each dataset used in training, validation and testing contained recordings from only a single session per participant. For the largest model, denoted with a separate marker in Fig. 2f, we used 4,800 training participants and we included multiple sessions of data when available (that is, many participants collected multiple repeats of the open-loop training protocol). This last point was not included in the fitting procedure for the scaling law, but this model was used in the closed-loop evaluations.
Discrete-gesture labels were obtained from the gesture prompts by first aligning them to the EMG using the algorithm described above in the ‘Discrete-gesture time alignment’ section. To facilitate gesture detection, we then shifted these labels forward in time by 100 ms to provide the model with a 100 ms longer context of sEMG signal before making a prediction. These shifted labels were used both in model training and for offline evaluation.
For offline evaluation, we first converted the logits outputted by the model into discrete-gesture predictions. Gesture predictions were triggered whenever the probability for any gesture went above the threshold value, set to 0.35 (based on a hyperparameter search using the validation set). These predictions were then filtered using three steps: debouncing, event matching and state-machine filtering. In debouncing, whenever a gesture was predicted within 50 ms of another gesture, the second gesture was removed. The sole exception was release events, which were not debounced when preceded by a different gesture, to ensure the inclusion of quick index/middle taps (that is, a press immediately followed by a release). In event matching, we matched ground-truth labels to model predictions using the Needleman–Wunsch algorithm for sequence alignment83. We included the constraint that ground-truth labels and model predictions can only be matched if their offset falls within a tolerance window of −50 to +250 ms (centred at the aforementioned +100 ms label shift). This provided us with a sequence of ground-truth events and a corresponding sequence of matching predicted events. The predicted events were then further processed with a state-machine filter, in which predicted release gestures were removed if the previous gesture in the ground truth sequence was not the expected press gesture (that is, index press for index release and middle press for middle release). State-machine filtering was done to avoid penalizing the model for mistaken release predictions that would not influence online performance, where releases were only used for index/middle holds, which first had to be triggered by a press (see the ‘Discrete gestures’ part of the ‘Online evaluation’ section below). Following this state-machine filtering step, we performed event matching again to match the ground truth gestures with the state-machine-filtered model predictions.
Given this sequence of ground truth gestures and matching predictions, we evaluated model performance with the classification error rate (CLER), defined as the proportion of ground-truth labels for which the matching prediction is incorrect. In calculating this metric, we ignored any ground-truth labels without a matching model prediction to reduce sensitivity to false negatives that can occur from participant noncompliance and for consistency with online metrics for which no prompt-based ground truth is available. We calculated CLER independently for each gesture and then aggregated these into a single value by taking the average of the nine per-gesture CLERs.
Architecture
The discrete-gesture network architecture took as input rescaled and high-pass filtered sEMG signal. sEMG was rescaled by 2.46 × 10−6, filtered through a 40 Hz high-pass filter (fourth-order Butterworth, as was done for the MPF features used for the other models; see the ‘MPF features’ section) and then passed through a sigmoidal function (\(f(x)=x/(\mu +| x| )\)) to reduce the effect of outliers, with μ = 32 (found to be performant through a hyperparameter sweep). The network architecture consisted of a 1D convolutional layer (with a stride of 10 to downsample the input from 2 kHz to 200 Hz), followed by a dropout layer with dropout probability 0.1, a layer norm layer, three LSTM layers with dropout probability 0.1 in between them, a second layer norm layer and a final linear readout layer with a sigmoid nonlinearity on top to predict the probability of each of the nine gestures (index/middle finger press and release, thumb tap and thumb left/right/up/down swipe). For the smaller model, the dimensions of the convolutional layer and the number of hidden units in the recurrent blocks were set to 128. For the larger model, they were set to 512. A forward pass of the larger architecture required 353,300 FLOPs per output sample.
Optimization
Networks were trained using the Adam optimizer. To mitigate divergence during training, gradient clipping was applied throughout. We additionally used a learning rate scheduler that linearly ramped up the learning rate from 5 × 10−7 to 5 × 10−4 over the first 5 epochs, and then decayed it by a factor of 0.5 every 25 epochs thereafter. For the smaller model, a larger learning rate was used: the maximum learning rate was ramped up from 10−6 to 10−3 and then decayed in the same way. For all models, we used a batch size of 512. Training was done using a multilabel binary cross-entropy loss, whereby each gesture is independently evaluated against its own absence. Each model was trained for a fixed wall clock duration equal to the time it took the largest model to reach convergence. Final checkpoints were selected based on the model that yielded the highest validation score, defined as a proxy of the CLER metric that can be run online. This proxy CLER is obtained by computing the argmax of the model output probabilities and comparing them against a temporal window (50 ms before–150 ms after) around each ground truth event. Training the largest model on the largest training set took 10 min per epoch, for a total of 12 h on an NVIDIA A10G Tensor Core GPU.
Handwriting
To train handwriting models, we used the CTC loss as described previously76. Notably, we used characters instead of phonemes for this purpose. The characters predicted included all lower-case letters [a-z], numbers [0-9], punctuation marks [,.?'!], and four gestures for text input control [space,dash,backspace,pinch]. When spaces were explicitly prompted with a right dash during data collection to perform a right index swipe gesture, model targets were both a <dash> and <space>, for example, “hello<dash><space>there”. In prompts where spaces were implicitly prompted, the model target was simply <space>, that is, “hello<space>there”. Moreover, we integrated a greedy implementation of the FastEmit regularization technique84. This regularization approach effectively reduced the streaming latency of our models by penalizing sequences of ‘blank’ outputs.
Nine training corpora were generated, each containing a varying number of participants ranging from 25 to 6,527 in a geometric sequence (excluding the last point). Each corpus was a superset of the previous corpus’s participants, ensuring that participants in the 25-participant corpus are also present in the 50-participant and 100-participant corpora, and so on. The participants were uniformly sampled without replacement from the entire corpus, preserving the distribution of data quantity per participant found in the full corpus. We used 100 held-out participants to create our evaluation corpora, which remained constant throughout our investigation. The validation corpus comprised data from 50 participants and was used for hyperparameter selection and early stopping during model training. The test corpus contained data from 50 participants and served for the final evaluation of each handwriting model’s generalization performance. We also used a subset of these 50 test participants for our personalization corpus (see the ‘Personalization experiments’ section).
Two primary data-augmentation strategies were used. The first involved SpecAugment75, which applies time- and frequency-aligned masks to spectral features during training. The second strategy involved rotational augmentation, randomly rotating all channels by either −1, 0 or +1 position uniformly. This meant that channel signals were shifted one channel to the left, remained unshifted or were all shifted to the right, respectively.
For evaluating the model’s offline performance for each user, we used the WPM and CER aggregated over all prompts collected for that user, for instance:
$${\rm{CER}}=\frac{{\sum }_{i}{\rm{edit}}\_{{\rm{distance}}}_{i}}{{\sum }_{i}{\rm{prompt}}\_{{\rm{length}}}_{i}},$$
where edit_distancei is the Levenshtein distance between the prompt and the model output for prompt i and prompt_lengthi is the length of the prompt.
Architecture
The handwriting network architecture took our custom MPF features of the sEMG signal as input. These features were passed through a rotational-invariance module, exactly as described for the wrist decoder above. The channel rotation in this module was performed in addition to the channel rotation data augmentation described above. The signal was then passed through a conformer30 architecture consisting of 15 layers. Each layer encompassed 4 attention heads and used a time-convolutional kernel with a size of 8. Throughout the conformer layer convolutional blocks, a stride of 1 was used, except for layers 5 and 10, where the stride was set to 2. To ensure that the model functioned in a streaming manner, a modified conformer architecture was used. This adaptation is similar to the approach outlined previously85, but with adjustments to ensure causality. Specifically, self-attention is solely applied to a fixed local window situated directly before the current time step. In our networks, the size of this attention window was 16 for the initial 10 conformer layers and then decreased to 8 for the subsequent 5 layers. Finally, the outputs from the conformer blocks were subjected to average pooling across channels. They were then passed through a linear layer, which projected the output to match the size of the character dictionary. A softmax function was applied thereafter. During decoding, the model’s best estimate at each output time step was greedily followed, and repeating characters in the prediction were removed to reduce the output.
In our investigation, we explored various trainable model parameter counts. We manipulated the parameter count of our models by adjusting the feed-forward dimension and input dimension within our conformer architecture. Importantly, we upheld a consistent 1:2 ratio between the input dimension and the feed-forward dimension in the conformer blocks. A forward pass of the larger architecture required 801.7 million FLOPs per output sample.
Optimization
The training of our conformer architecture was executed using AdamW as the optimization algorithm. This process spanned a maximum of 200 epochs and involved a learning rate set at 6 × 10−4 for the 1 million parameter model and 3 × 10−4 for the 60 million parameter model, both with a weight decay of 5 × 10−2. A cosine annealing learning rate schedule was implemented, featuring a warm-up period lasting 1,500 steps and a minimum learning rate of 0. Our chosen batch size was a total of 512 across 32 processes each with a batch size of 16, wherein each sample within the batch represented a prompt that was zero-padded to match the length of the longest prompt within that batch. To prevent gradient explosion, we applied gradient clipping with a norm threshold of 0.1 throughout the training process. The training length was chosen to ensure that models trained would converge at all training corpus scales by visually inspecting past experimentation of similar experiments. Other hyperparameters such as learning rate, weight decay, learning rate schedule and gradient clipping were determined based on previous hyperparameter searches optimizing performance on the 50 participant validation corpus. Lastly, we assessed the test performance of the training checkpoint corresponding to the lowest validation CER. Training the largest model on the largest training set took 33 min per epoch, for a total of 4 days 17 h on 4 NVIDIA A10G Tensor Core GPU running a distributed data parallel pipeline.
Generic decoder scaling laws
Fitted function
In Fig. 2d–f, we show the fits of the generic error scaling with the number of training participants. The fits follow a functional form taken from the large language model literature31, where the error is a function of both model size (D, in number of parameters) and data quantity (N, in number of participants):
$$Er=e+{A}_{N}/{N}^{{\alpha }_{N}}+{A}_{D}/{D}^{{\alpha }_{D}}$$
where all fitted parameters are positively bounded. It is generally understood that the e term in this equation is the irreducible error of the task and the second and third terms both contribute to the error reduction as N and D are increased, respectively. Note that there exist diminishing return regimes if either N or D are increased individually, as the other term fixes the asymptotic error floor. Also note that the definitions of N and D are swapped relative to ref. 31.
Fitting procedure
A single set of parameters fits all of the observed points in each graph, with the exception of the heterogeneous datapoint in the discrete-gesture experiments that we keep held out because of its training corpus distinction with the rest of the points. The fitted parameters were obtained by minimizing the mean squared logarithmic error (MSLE) using the L-BFGS-B optimization algorithm86 along with 200 iterations of the basin hopping strategy87. The initial guess and the bounds for the fitted parameters are shown in Supplementary Table 1.
Online evaluation
Task participants and structure
For online studies, we recruited participants who had no prior experience with the sEMG task being studied and, in the majority of cases, had no previous experience with sEMG. Demographic information about these participants is provided in Extended Data Fig. 8f–i.
All closed-loop experiments were structured into three blocks: practice block, evaluation block 1 and evaluation block 2. During the practice block, the participants were explicitly instructed to explore performing the required gestures/movements in different ways to understand how to best perform the task. During the evaluation blocks, the participants were instructed to be as fast and accurate as possible.
Coaching
During the practice block of online experiments, we provided explicit verbal and demonstrative coaching to guide the participants towards styles of movement that were known to be well-suited for the given sEMG decoder. For the wrist decoder and discrete-gestures decoder, coaching was provided for about 20–25% of participants, who did not perform the gestures as expected; for example, by pronating their forearm while flexing their wrist, or by performing thumb swipes too slowly. For the handwriting decoder, we found that initial coaching was given to the majority (around 80%) of participants as they tended to write individual characters slowly and deliberately, a style that did not always trigger the sEMG decoder. We explicitly instructed these participants to write faster and more smoothly, as if they were writing with a pen. For some participants, it was also useful to explore a few different postures to facilitate writing in this style despite the lack of a pen and paper. During the evaluation blocks, further coaching was only provided when necessary if the participant was stuck on a given trial, for example, if a participant could not complete a given gesture in the discrete grid navigation task or could not write a given word or character in the handwriting task. We found that this was only necessary for a minority of participants with the discrete gestures and handwriting decoders. For the wrist decoder, we also instructed users to make quick wrist deflections whenever they observed significant drift between the decoder’s predictions and their perceived wrist angle. Such quick deflections tended to fix this drift and allow the participant to proceed at higher performance. Any time spent on this is subsumed in the acquisition time and dial-in time metrics.
Wrist
To evaluate continuous closed-loop control with the wrist decoder, users first completed a calibration procedure (rapid wrist flexions and extensions) to determine their minimum and maximum wrist angle velocities predicted by the decoder, vmin, vmax. Model outputs, vt, were then normalized to these values using a normalization function, ηt, and scaled by a constant velocity gain, gv, and handedness normalization parameter, h. To estimate the cursor position, we integrated the velocity starting from x0 = 0 at the start of the session to determine the unbounded horizontal cursor position, \({\mathop{x}\limits^{ \sim }}_{t}\), and the cursor position bounded by the edges of the workspace, xt:
$$\begin{array}{c}{\mathop{x}\limits^{ \sim }}_{t}={x}_{t-1}+h\frac{{g}_{{\rm{v}}}}{{\eta }_{t}}{v}_{t}\\ {x}_{t}=\text{min}(\text{max}({\mathop{x}\limits^{ \sim }}_{t},\,-1),\,1)\\ {\eta }_{t}={v}_{\text{max}}\varTheta ({v}_{t})+{v}_{\text{min}}(1-\varTheta ({v}_{t}))\end{array}$$
where Θ(⋅) is the Heaviside function. We used gain gv = 0.75 normalized pixels per radian (determined empirically to work well for comfortable closed-loop control) and set h = 1 if the sEMG wristband is on the right hand (so that wrist flexion/extension maps to left/right, respectively) and −1 if it is on the left hand (so that wrist flexion/extension maps to right/left, respectively). The second equation ensured that the horizontal cursor position, xt, was bounded to the left and right edges of the workspace, −1 and 1.
Before engaging in the online evaluation task, the minimum and maximum wrist angle velocities obtained from the calibration procedure were verified by asking the user to move the cursor in an empty workspace. If they were unable to hit the edges of the workspace, the calibration procedure was repeated to get a better estimate of vmin, vmax. This was necessary for 3 out of 17 participants.
We evaluated cursor-control performance using the same horizontal cursor-to-target task described under the ‘Wrist corpus’ section above. In brief, in each trial, the participant was prompted to move the cursor to 1 out of 10 equally sized rectangular targets presented on a horizontal grid, with the outer edges of the leftmost and rightmost targets touching the left and right edges of the workspace (±1). A target was acquired by hovering over it for 500 ms (Fig. 3a, Extended Data Fig. 7a and Supplementary Video 1). Once all 10 targets were acquired, a new set of 10 targets was presented, and each one was prompted in a random sequence. This was repeated 5 times in each block, for a total of 50 trials per block, where one trial corresponds to one target presentation and acquisition. The cursor position was continually decoded from sEMG throughout the session and never reset between trials or blocks.
We first quantified performance using the acquisition time per trial, which is the time taken to acquire the target, not including the 500 ms hold time. In other words, the acquisition time is the trial duration minus the 500 ms hold time. All trials with acquisition times below 200 ms were discarded (29 out of 2,550 trials, or 1.1%), as this is below typical human reaction times88. Such trials sometimes occurred when, by chance, the next prompted target happened to be immediately next to the current cursor position and the cursor happened to be moving in that direction. Figure 3d shows the mean acquisition time over all non-discarded trails in each block, for each participant. Note that this average is over trials with varying starting distances from the target. In Extended Data Fig. 8a, we further examine performance in this task using Fitts’ law throughput89, which accounts for trial-to-trial differences in reach distances and has been previously used in HCI90 and BCI settings5.
An additional measure that we used to quantify performance was the dial-in time (Fig. 3e), which is a measure of precise control around the target, adapted from the BCI literature91. Dial-in time was measured as the time from the first target entry to the last target entry, not including the 500 ms target hold time. Figure 3e shows the mean dial-in time over all non-discarded trials in which the cursor prematurely exited the target before completing the 500 ms hold time (that is, trials in which the dial-in time was greater than 0).
Discrete gestures
To evaluate the discrete-gesture decoder, we used a discrete grid navigation task in which each of the thumb swipes (left/right/up/down) was used to move a yellow circular character, named Chomper, along a discrete grid (Fig. 3b, Extended Data Fig. 7b and Supplementary Video 2). Movements were prompted with a series of targets indicating the direction in which Chomper should move and, every few steps, the participant was prompted to perform one of the three ‘activation’ gestures: thumb tap, index hold or middle hold.
A given gesture detection was triggered whenever the model output probability of a given gesture rose above a threshold value of 0.5. As in the offline setting, these gesture detections were filtered by debouncing and state machine filtering. The only differences with the offline setting, were that the state machine (1) removed release gestures preceded by any event other than the corresponding press and (2) synthetically added a corresponding release gesture whenever a press event was followed by any event other than the corresponding release. Index/middle holds were defined as a press followed by a release at least 500 ms later.
We defined a ‘trial’ as a randomly sampled sequence of targets and activation prompts requiring 8 thumb swipes and 5 activations. If the model detected a thumb swipe in the wrong direction, Chomper would move in the detected direction and the participant would therefore be prompted to swipe in the opposite direction to move Chomper back to its previous position. The total number of prompted thumb swipe gestures in each trial could therefore vary depending on how many times the wrong thumb swipe direction was detected. Incorrect activation gesture detections would be indicated to the participant, but would not alter Chomper’s position. If, on an index or middle hold prompt, the release followed the press less than 500 ms later, this was classified as an ‘early release’ error. The participants performed ten trials in each block and were explicitly instructed to favour accuracy over speed when performing the task.
Completion rate (Fig. 3g) was defined as the minimum number of discrete gestures required to complete a trial (8 thumb swipes + 5 activations = 13 gestures) divided by the time required to complete a trial. Mistakenly making additional gestures that were counterproductive to completing the trial added to the time required, but did not increase the number of required gestures. To calculate the confusion matrix for each participant, we counted the number of times that each gesture was detected when a given gesture was expected. To get a proportion, we then divided this by the total number of gestures executed when that given gesture was expected. Figure 3h shows the average confusion matrix across all participants, using the trials in the two evaluation blocks only. The first hit probability (Fig. 3f) was calculated by taking the proportion of prompted gestures in which the first executed gesture was the expected one. For both the first hit probability and the confusion matrix metrics, we included the 13 prompted gestures in each trial as well as any additional prompted thumb swipes resulting from swiping in the wrong direction.
Note that, to complete the discrete-gesture task, the participant was required to perform all gestures correctly. Therefore, before this task began, all of the participants were screened to confirm that each gesture worked for them; however, no participants had prohibitive issues with any gesture.
Handwriting
To evaluate the handwritten character decoder in a closed loop, we used a handwriting task in which, in each trial, the participants were prompted to handwrite a five-word phrase randomly sampled from the Mackenzie corpus92. Characters ([a-z], [0-9], [space], [,.?'!_]) and a single gesture ([space]) were decoded online with the decoder and displayed to the participant in real time (Fig. 3c, Extended Data Fig. 7c and Supplementary Video 3). The participants were instructed to ensure that the decoded phrase was understandable before submitting it and moving on to the next trial. If the participant produced any incorrect characters, they could use the backspace key on the keyboard to erase errors and then rewrite them. Trials were completed when the participants made their best attempt to write the prompted phrase and then submitted the written text by pressing a key on the computer keyboard using their non-dominant hand. Each block consisted of ten trials.
In our analysis, we report the median CER and WPM over all trials in each block. For each trial i, we calculate the CER according to a previous study33:
$${{\rm{CER}}}_{i}=\frac{{\rm{edit}}\_{{\rm{distance}}}_{i}}{\max \{{{\rm{prompt}}\_{\rm{length}}}_{i},{\rm{output}}\_{{\rm{length}}}_{i}\}},$$
where edit_distancei is the Levenshtein distance between the prompt and the model output submitted by the user in trial i, prompt_lengthi is the length of the prompt and output_lengthi is the length of the model output. The maximum between these two is used in the denominator to ensure that the CERi is between 0 and 1. For WPM, we assume an average of 5 characters per word (including spaces), so we determine the number of words in each prompt by counting the total number of written characters and dividing this by 5. We measured the prompt duration with the time elapsed between the first and last character emission from the model during that trial, to remove any time spent reading the prompt or clicking the submit button to advance onto the next prompt.
For each user and block in Fig. 3i,j, we calculate the CERi and WPM independently for each trial and report the median over trials. Note that this online CER metric is therefore not directly comparable with the offline CER metric reported in Fig. 2g, which was calculated by aggregating errors over all prompts (see the ‘Handwriting’ part of the ‘Generic sEMG decoder modelling’ section). Computing the median over trials was necessary for quantifying online performance due to the presence of outlier trials with poor performance (for example, due to accidentally pressing the submit button before completing the prompt), which had an outsize influence on the aggregate number of errors in each block due to the small sample size of ten trials per block.
Generic sEMG decoder baselines
Wrist
As baseline performance for the sEMG wrist decoder (Fig. 3d,e (dashed red line)), we used horizontal cursor-to-target task performance from the wrist corpus, in which the cursor was controlled by the ground truth wrist angle tracked through motion capture (see the ‘Wrist corpus’ section). This offers a behaviourally controlled comparison for our EMG model because it uses the same instructed wrist movement. The cursor position was determined by scaling the normalized and centred ground truth flexion/extension wrist angle by a constant gain. For our baseline, we use the cursor-to-target task with the horizontal target configuration and a gain of 2.0, as we found performance was slightly higher than with the larger gain of 4.0.
For each metric in Fig. 3d,e, we calculate the mean over all 50 trials for each participant in the wrist corpus (n = 162) and report the median over participants. This pool of participants is non-overlapping with the participants who performed the sEMG wrist decoder online evaluation task. For those participants who recorded multiple datasets, we used only the data from the first session and discarded the second session, to eliminate learning effects from having been previously exposed to the task. Note that performance may therefore be slightly lower than it would be after more extensive practice, as in the case in the online evaluation experiment where participants performed a practice block of 50 trials before performing the evaluation blocks.
To contextualize wrist-based control performance with a more conventional interface, we also measured performance on this task using a MacBook trackpad. In this case, the cursor’s horizontal position was set to that of the native laptop mouse controlled by the trackpad, with default trackpad settings. The vertical position of the cursor was fixed to the height of the targets at all times. The same n = 17 participants who performed the wrist decoder online evaluation study subsequently performed 50 trials of the same cursor-to-target game under trackpad control, and we measured metrics over these 50 trials to obtain the baseline values reported above. Note that participants therefore had 150 trials of experience with this task (while using the sEMG wrist angle decoder) before performing it with the trackpad.
Discrete gestures
As the baseline performance for the discrete-gesture decoder, we used performance on the discrete grid navigation task using a commercially available Nintendo Switch Joy-Con controller. This device enables us to evaluate the baseline performance without an sEMG decoder while still requiring similar one-handed motions to those required by the discrete-gesture decoder. We mapped controller buttons to the discrete gestures used in the task as follows: left/right/up/down thumb swipes were replaced by analogous joystick movements, thumb taps were replaced by pressing the ‘b’ button just above the joystick, and index and middle press and release were replaced by upper and lower bumper press and release, respectively. To avoid simultaneous inputs, no other gestures were decoded after a button press until that button was released. Left/right/up/down joystick movements were detected any time the joystick x or y value exceeded 15% of its maximum value. Once a joystick movement was detected, the total distance travelled along the x and y axes was compared and the direction of the movement was determined from the axis with greater distance travelled. While all interactions were one-handed, the Joy-Con controller was mounted in a commercially available Nintendo Switch Joy-Con grip, to allow participants to hold the controller with two hands if this improved their comfort.
A different set of n = 23 participants performed this task, non-overlapping with the participants who performed the sEMG discrete-gesture decoder online evaluation task. Apart from changes to controller-specific prompts and instructions, the discrete grid navigation task and performance metrics used were otherwise identical to those for the sEMG discrete-gesture decoder. The participants were also screened to confirm that each button worked for them, following exactly the same procedure as for the EMG decoder. As baseline values in Fig. 3f,g, we used median performance in the last evaluation block, which we found to be the block with highest performance (Extended Data Fig. 8b,c).
Handwriting
To generate a baseline of handwriting speed, we calculated how fast people wrote during the ‘phrases’ portion of offline data collection used for training and testing the Handwriting model (see the ‘Handwriting corpus’ section). We used a set of n = 75 participants for this purpose, non-overlapping with the participants who performed the sEMG handwriting decoder online evaluation task. Each of these participants were prompted to handwrite a selection of phrases on top of a Sensel Morph touch surface device, without a pen. This device was used to measure the time taken to write a prompt, by using the time elapsed between the first touch on and last lift off the surface over the duration of the prompt. Using only the prompt start and end times resulted in a lower WPM (21 WPM), reflecting the latency for a participant to initiate writing after a prompt appeared and to advance to the next prompt once complete. For consistency with the WPM metric used to evaluate the sEMG decoder, we counted the number of words in a prompt by counting the total number of characters (including spaces) and dividing by 5.
Discrete-gesture detection model investigation
Network convolutional filter analysis
To examine the initial Conv1d layer of the trained discrete-gesture decoder, we first measured various spatiotemporal properties of each of the Conv1d filter weights. Each filter is a spatiotemporal weight matrix of shape 16 input channels × 21 timesteps. It produces one output feature by convolving each row of the weight matrix with the corresponding sEMG-RD channel and summing the outputs over the rows. Below, we refer to each row as an input channel.
We first measured the RMS power of each input channel and identified the input channel with maximum power. We then measured the temporal frequency response of this max input channel using a discrete Fourier transform and identified the peak frequency with strongest magnitude response. We measured the bandwidth of the temporal frequency response as the range of contiguous frequencies around this peak that had a magnitude response within 50% of the peak. We additionally counted how many input channels had RMS power within 50% of the max channel. The distributions of these metrics across all Conv1d filters are shown in Extended Data Fig. 9.
We next identified the set of Conv1d filters that fell within the interquartile range of these three metrics (peak frequency, bandwidth, number of active channels), and randomly selected six filters with different peak channels. These are the representative examples shown in Fig. 4b,d,e. The six putative MUAPs shown in Fig. 4c were extracted using the procedure described in the section ‘Putative motor unit action potential waveform estimation’ and Extended Data Fig. 2, and then the raw EMG signal in the central 10 ms of each snippet was high-pass filtered with the same preprocessing procedure applied to the discrete-gesture model training data (see the section ‘Architecture’ under ‘Generic sEMG decoder modelling’). This allowed a direct comparison with the 10 ms convolutional filters trained on data preprocessed in this way. The same procedure for measuring RMS power and frequency response was applied to the six putative MUAPs after this preprocessing to obtain the curves shown in Fig. 4d,e.
Discrete-gesture detection network LSTM representation analysis
To examine the LSTM representations of the trained discrete-gesture decoder, we used recordings from 3 different sessions from each of 50 randomly selected users from the test set. From each of these recording sessions, we randomly sampled forty 500 ms sEMG snippets ending at labels for each gesture class (after label timing alignment; see the ‘Discrete-gesture time alignment’ section), for a total of 40 × 9 = 360 sEMG snippets per session. We then passed each of these snippets through the trained discrete-gesture decoder, with the LSTM state initialized to zeros, to obtain vector representations, X ∈ \({\mathbb{R}}\)512, of each snippet. PC projections of the vectors from three randomly selected users are plotted in Fig. 4f–h, in each case coloured by a different property. Gesture-evoked sEMG power was measured as the RMS of the last 100 ms of each sEMG snippet. For each participant and gesture, this was then binned into 20 bins with a matched number of snippets, dividing the sEMG power into the categories plotted in Extended Data Fig. 8l.
To quantify the structure in these representations, we used the proportion of variance in LSTM representations accounted by a given variable, ξ:
$${{\rm{Var}}}_{\xi }[{E}_{X}[X| \xi ]]/{{\rm{Var}}}_{X}[X].$$
The numerator is the variance in the mean representations of each category of ξ, and the denominator is the total variance of the representations. In each case, variance is calculated as the trace of the covariance of the representations. For the discrete-gesture identity and participant-identity analysis, we divided the 50 participants into 10 non-overlapping sets of 5 participants and calculated the proportion of variance separately for each set. The curves in Fig. 4i show the mean and 95% confidence interval over these 10 sets. For the band placement and gesture-evoked sEMG power curves, the proportion was calculated separately for each of the 50 participants, and the mean and 95% confidence interval over participants was shown. For this analysis, the sEMG power was binned as indicated above but into only 3 bins (low/medium/high) rather than 20.
Personalized modelling
We studied the personalization of handwriting models with 40 participants from the test corpus that were held out from the 6,527 participants in the pretraining corpus. For each participant, we further trained, that is, fine-tuned, a chosen generic handwriting model on a fixed budget of data solely taken from that participant’s sessions. The resulting personalized model was then evaluated on held-out data from the same participant on whom it was personalized. We considered personalization data budgets of 1, 2, 5, 10 and 20 min. We repeated this process for each of our 40 participants and reported the population average of the personalized model performance.
Data
We created a training and testing set for each of our 40 personalization participants by holding out three sessions for the test set, with each session containing data collected in one of the three postures (seated writing on a surface, seated writing on their leg and standing writing on their leg). The remaining sessions for that user were included in the training set, subsampled to obtain the desired number of minutes of labelled sEMG recording. The subsampling was done through random uniform sampling of the prompts from all of the sessions in the training set. Each subsample of the full training set was a superset of the preceding data budget size, ensuring that the prompts in the 1 min budget were also present in the 2 min and 5 min budget, and so on.
Optimization
The optimization details closely resemble the procedure followed for generic training (see the ‘Handwriting’ section under ‘Generic sEMG decoder modelling’) with a few differences. We used a cosine annealing learning rate schedule without warmup. We also varied the fine-tuning learning rate as a function of the number of pretraining participants used to pretrain the upstream generic model, such that: LR(N) = 1.24 × 10−5 × N−0.42, with N being the number of pretraining participants. The learning rate relationship with generic pretraining participants was found through grid learning rate sweeps for the models pretrained on 25, 400 and 6,527 participants, then fitting a power law to the population average performance minima found. We did not use weight decay during fine-tuning. We fine-tuned the model for 300 epochs, at a batch size of 256, with no early stopping such that the training is always 300 epochs.
Statistics
In Fig. 5e, we found negative transfer of personalized models across participants. To characterize each participant’s performance on other fine-tuned models, we first computed the mean of each row without the diagonal. We then computed the median of the means along with the s.e.m. This was compared with the median of the diagonal values.
In Extended Data Fig. 10, we added early stopping to the personalization procedure to disambiguate the contribution of increased personalized data budget per user from an increase in the number of fine-tuning iterations. We found very similar results with (Extended Data Fig. 10) and without (Fig. 5) early stopping, except that a few of the best performing users exhibited regressions from personalization without early stopping. This verified that the benefits from including more personalization data were not due to an increase in training iterations. Note that, in practice, early stopping would require additional data from the participant to use for validation. Here we used the test set for early stopping, so the results in Extended Data Fig. 10 should be considered validation numbers.
Personalization scaling laws
Fitted function
In Fig. 5b, we show the fits of the 60.2 million parameter model error rate as a function of the number of pretraining participants for the generic model and for each personalization data budget. We used a simple power law fit with respect to pretraining data quantity (N, number of pretraining participants), such that:
$$Er=e+A/{N}^{\alpha }.$$
We did not include the contribution from model size, as we only fitted observations from a single model size (the error from finite model size was therefore absorbed into e).
Fitting procedure
The fitted parameters for each personalization data budget were obtained by minimizing the MSLE using the L-BFGS-B optimization algorithm86 along with 200 iterations of the basin hopping strategy87. The initial guess and the bounds for the fitted parameters are shown in Supplementary Table 2.
Personalization equivalence calculations
Relative increase calculation
To determine the equivalent pretraining participant budget needed to match a given personalization performance, we needed a continuous estimate of generic model performance as a function of the number of pretraining participants. For this, we used logspace piecewise linear interpolation of the generic performance values, which we denote by fgeneric(N). Given the number of pretraining participants, N, and personalization minutes, m, personalized models have an observed CER given by CER(N,m). To find the equivalent additional pretraining participants ΔN needed to match performance between generic and personalized models we set fgeneric(N + ΔN) = CER(N,m) and solve for ΔN using the Newton conjugate-gradient method. This gives the points in Fig. 5d. Overlaid on the plot as dotted lines, we used the power law fit of the points corresponding to each number of personalization minutes in Fig. 5b to infer continuous curves of equivalent fold-increase in pretraining data required using the approach described above.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
We have publicly released 1,060 sEMG recordings from 300 participants spanning the 3 tasks in the study: 100 participants (74 h) of wrist data, 100 participants (63 h) of discrete gestures data and 100 participants (126 h) of handwriting data. Each participant was randomly selected from the set of training users described in the study. We also provide labels, gesture times and regression targets for these datasets. All data are anonymized and contain no identifying information. The data are hosted online (https://fb-ctrl-oss.s3.amazonaws.com/generic-neuromotor-interface-data).
Code availability
We have also published a GitHub repository (https://github.com/facebookresearch/generic-neuromotor-interface-data) with implementations of the models described in the manuscript for wrist, handwriting and discrete gesture tasks. We also provide a framework for training and evaluating models on the data that we have released. Data and code are available under a Attribution-NonCommercial-ShareAlike 4.0 license. Instructions for downloading the data, training models and evaluating models can be found in the site’s README file.
References
Battye, C. K., Nightingale, A. & Whillis, J. The use of myo-electric currents in the operation of prostheses. J. Bone Joint Surg. Br. 37-B, 506–510 (1955).
Hochberg, L. R. et al. Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature 485, 372–375 (2012).
Collinger, J. L. et al. High-performance neuroprosthetic control by an individual with tetraplegia. Lancet 381, 557–564 (2013).
Willett, F. R. et al. A high-performance speech neuroprosthesis. Nature 620, 1031–1036 (2023).
Gilja, V. et al. A high-performance neural prosthesis enabled by control algorithm design. Nat. Neurosci. 15, 1752–1757 (2012).
Abiri, R., Borhani, S., Sellers, E. W., Jiang, Y. & Zhao, X. A comprehensive review of EEG-based brain-computer interface paradigms. J. Neural Eng. 16, 011001 (2019).
Kerous, B., Skola, F. & Liarokapis, F. EEG-based BCI and video games: a progress report. Virtual Real. 22, 119–135 (2018).
Défossez, A., Caucheteux, C., Rapin, J., Kabeli, O. & King, J.-R. Decoding speech perception from non-invasive brain recordings. Nat. Mach. Intel. 5, 1097–1107 (2023).
Brandman, D. M., Cash, S. S. & Hochberg, L. R. Human intracortical recording and neural decoding for brain-computer interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 25, 1687–1696 (2017).
Lotte, F. et al. A review of classification algorithms for EEG-based brain-computer interfaces: a 10 year update. J. Neural Eng. 15, 031005 (2018).
Degenhart, A. D. et al. Stabilization of a brain-computer interface via the alignment of low-dimensional spaces of neural activity. Nat. Biomed. Eng. 4, 672–685 (2020).
Brandman, D. M. et al. Rapid calibration of an intracortical brain-computer interface for people with tetraplegia. J. Neural Eng. 15, 026007 (2018).
Kandel, E. R., Schwartz, J. H., Jessell, T. M., Siegelbaum, S. A. & Hudspeth, A. J. Principles of Neural Science, Fifth Edition Vol. 4 (McGraw-Hill Medical, 2000).
De Luca, C. J. The use of surface electromyography in biomechanics. J. Appl. Biomech. 13, 135–163 (1997).
Pullman, S. L., Goodin, D. S., Marquinez, A. I., Tabbal, S. & Rubin, M. Clinical utility of surface EMG: report of the therapeutics and technology assessment subcommittee of the American Academy of Neurology: report of the Therapeutics and Technology Assessment Subcommittee of the American Academy of Neurology. Neurology 55, 171–177 (2000).
Campanini, I., Disselhorst-Klug, C., Rymer, W. Z. & Merletti, R. Surface EMG in clinical assessment and neurorehabilitation: barriers limiting its use. Front. Neurol. 11, 934 (2020).
Farina, D. et al. The extraction of neural information from the surface EMG for the control of upper-limb prostheses: emerging avenues and challenges. IEEE Trans. Neural Syst. Rehabil. Eng. 22, 797–809 (2014).
Scheme, E. & Englehart, K. Electromyogram pattern recognition for control of powered upper-limb prostheses: state of the art and challenges for clinical use. J. Rehabil. Res. Dev. 48, 643–659 (2011).
Biddiss, E. A. & Chau, T. T. Upper limb prosthesis use and abandonment: a survey of the last 25 years: a survey of the last 25 years. Prosthet. Orthot. Int. 31, 236–257 (2007).
Scheme, E., Fougner, A., Stavdahl, Ø., Chan, A. D. C. & Englehart, K. Examining the adverse effects of limb position on pattern recognition based myoelectric control. In Proc. IEEE Eng. Med. Biol. Soc. 6337–6340 (IEEE, 2010).
Phinyomark, A. & Scheme, E. EMG pattern recognition in the era of big data and deep learning. Big Data Cogn. Comput. 2, 21 (2018).
Young, A. J., Hargrove, L. J. & Kuiken, T. A. The effects of electrode size and orientation on the sensitivity of myoelectric pattern recognition systems to electrode shift. IEEE Trans. Biomed. Eng. 58, 2537–2544 (2011).
Zia Ur Rehman, M. et al. Multiday EMG-based classification of hand motions with deep learning techniques. Sensors 18, 2497 (2018).
Saponas, T. S., Tan, D. S., Morris, D. & Balakrishnan, R. Demonstrating the feasibility of using forearm electromyography for muscle-computer interfaces. In Proc. SIGCHI Conference on Human Factors in Computing Systems 515–524 (ACM, 2008).
Côté-Allard, U. et al. Deep learning for electromyographic hand gesture signal classification using transfer learning. IEEE Trans. Neural Syst. Rehabil. Eng. 27, 760–771 (2019).
Jiang, S. et al. Feasibility of wrist-worn, real-time hand, and surface gesture recognition via sEMG and IMU sensing. IEEE Trans. Industr. Inform. 14, 3376–3385 (2018).
Mendez Guerra, I., Barsakcioglu, D. Y., Vujaklija, I., Wetmore, D. Z. & Farina, D. Far-field electric potentials provide access to the output from the spinal cord from wrist-mounted sensors. J. Neural Eng. 19, 026031 (2022).
Merletti, R. & Farina, D. Surface Electromyography: Physiology, Engineering, and Applications (John Wiley & Sons, 2016).
Sussillo, D., Stavisky, S. D., Kao, J. C., Ryu, S. I. & Shenoy, K. V. Making brain-machine interfaces robust to future neural variability. Nat. Commun. 7, 13749 (2016).
Gulati, A. et al. Conformer: convolution-augmented transformer for speech recognition. In Proc. Interspeech 5036–5040 (ISCA, 2020).
Hoffmann, J. et al. An empirical analysis of compute-optimal large language model training. In Proc. Advances in Neural Information Processing Systems 30016–30030 (NeurIPS, 2022).
Zhai, X., Kolesnikov, A., Houlsby, N. & Beyer, L. Scaling vision transformers. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition 12104–12113 (Computer Vision Foundation, 2022).
Palin, K., Feit, A. M., Kim, S., Kristensson, P. O. & Oulasvirta, A. How do people type on mobile devices? Observations from a study with 37,000 volunteers. In Proc. 21st International Conference on Human-Computer Interaction with Mobile Devices and Services 1–12 (ACM, 2019).
McGraw, I. et al. Personalized speech recognition on mobile devices. In Proc. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 5955–5959 (IEEE, 2016).
Mdhaffar, S., Tommasi, M. & Estève, Y. Study on acoustic model personalization in a context of collaborative learning constrained by privacy preservation. Speech Comput. 12997, 426–436 (2021).
Eskimez, S. E. et al. Personalized speech enhancement: new models and comprehensive evaluation. In Proc. 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 356–360 (IEEE, 2022).
Wen, H., Ramos Rojas, J. & Dey, A. K. Serendipity: finger gesture recognition using an off-the-shelf smartwatch. In Proc. 2016 CHI Conference on Human Factors in Computing Systems 3847–3851 (ACM, 2016).
Amma, C., Georgi, M. & Schultz, T. Airwriting: a wearable handwriting recognition system. Pers. Ubiquitous Comput. 18, 191–203 (2014).
Mendez, I. et al. Evaluation of the Myo armband for the classification of hand motions. In Proc. 15th IEEE International Conference on Rehabilitation Robotics 1211–1214 (2017).
Tripathi, A., Prathosh, A. P., Muthukrishnan, S. P. & Kumar, L. SurfMyoAiR: a surface electromyography-based framework for airwriting recognition. IEEE Trans. Instrum. Meas. 72, 1–12 (2023).
Laput, G., Xiao, R. & Harrison, C. ViBand: high-fidelity bio-acoustic sensing using commodity smartwatch accelerometers. In Proc. 29th Annual Symposium on User Interface Software and Technology 321–333 (ACM, 2016).
Zhang, Y. & Harrison, C. Tomo: wearable, low-cost electrical impedance tomography for hand gesture recognition. In Proc. 28th Annual ACM Symposium on User Interface Software & Technology 167–173 (ACM, 2015).
Laput, G., Yang, C., Xiao, R., Sample, A. & Harrison, C. EM-Sense: touch recognition of uninstrumented, electrical and electromechanical objects. In Proc. 28th Annual ACM Symposium on User Interface Software & Technology 157–166 (ACM, 2015).
Iravantchi, Y., Goel, M. & Harrison, C. BeamBand: hand gesture sensing with ultrasonic beamforming. In Proc. 2019 CHI Conference on Human Factors in Computing Systems 1–10 (ACM, 2019).
Barona López, L. I., Ferri, F. M., Zea, J., Valdivieso Caraguay, Á. L. & Benalcázar, M. E. CNN-LSTM and post-processing for EMG-based hand gesture recognition. Intel. Syst. Appl. 22, 200352 (2024).
Benalcazar, M. E., Barona, L., Valdivieso, L., Aguas, X. & Zea, J. EMG-EPN-612 dataset. Zenodo https://doi.org/10.5281/ZENODO.4023305 (2020).
Eddy, E., Campbell, E., Bateman, S. & Scheme, E. Understanding the influence of confounding factors in myoelectric control for discrete gesture recognition. J. Neural Eng. 21, 036015 (2024).
Maslova, O. et al. Non-invasive EEG-based BCI spellers from the beginning to today: a mini-review. Front. Hum. Neurosci. 17, 1216648 (2023).
Jayaram, V. & Barachant, A. MOABB: trustworthy algorithm benchmarking for BCIs. J. Neural Eng. 15, 066011 (2018).
Lawhern, V. J. et al. EEGNet: a compact convolutional neural network for EEG-based brain-computer interfaces. J. Neural Eng. 15, 056013 (2018).
Sussillo, D. et al. A recurrent neural network for closed-loop intracortical brain-machine interface decoders. J. Neural Eng. 9, 026027 (2012).
Metzger, S. L. et al. A high-performance neuroprosthesis for speech decoding and avatar control. Nature 620, 1037–1046 (2023).
Musk, E. & Neuralink, An integrated brain-machine interface platform with thousands of channels. J. Med. Internet Res. 21, e16194 (2019).
Despradel Rumaldo, D. et al. Enabling advanced interactions through closed-loop control of motor unit activity after tetraplegia. In Proc. 37th Annual ACM Symposium on User Interface Software and Technology Vol. 19, 1–3 (ACM, 2024).
Formento, E., Botros, P. & Carmena, J. M. Skilled independent control of individual motor units via a non-invasive neuromuscular-machine interface. J. Neural Eng. 18, 066019 (2021).
Bräcklein, M., Ibáñez, J., Barsakcioglu, D. Y. & Farina, D. Towards human motor augmentation by voluntary decoupling beta activity in the neural drive to muscle and force production. J. Neural Eng. 18, 016001 (2021).
Radhakrishnan, S. M., Baker, S. N. & Jackson, A. Learning a novel myoelectric-controlled interface task. J. Neurophysiol. 100, 2397–2408 (2008).
Marshall, N. J. et al. Flexible neural control of motor units. Nat. Neurosci. 25, 1492–1504 (2022).
Yamagami, M., Portnova-Fahreeva, A. A., Kong, J., Wobbrock, J. O. & Mankoff, J. How do people with limited movement personalize upper-body gestures? Considerations for the design of personalized and accessible gesture interfaces. In Proc. 25th International ACM SIGACCESS Conference on Computers and Accessibility 1–15 (ACM, 2023).
Mugler, E. M. et al. Myoelectric computer interface training for reducing co-activation and enhancing arm movement in chronic stroke survivors: a randomized trial. Neurorehabil. Neural Repair 33, 284–295 (2019).
Henninger, F., Shevchenko, Y., Mertens, U. K., Kieslich, P. J. & Hilbig, B. E. lab.js: a free, open, online study builder. Behav. Res. Methods 54, 556–573 (2022).
Rastogi, A., Zang, X., Sunkara, S., Gupta, R. & Khaitan, P. Towards scalable multi-domain conversational agents: the schema-guided dialogue dataset. In Proc. 34th Conf. AAAI Artif. Intell. 8689–8696 (AAAI, 2020).
Chang, J. P. et al. ConvoKit: A toolkit for the analysis of conversations. In Proc. 21th Annual Meeting of the Special Interest Group on Discourse and Dialogue (eds Pietquin, O. et al.) 57–60 (ACM, 2020).
Harrison, V. F. & Mortensen, O. A. Identification and voluntary control of single motor unit activity in the tibialis anterior muscle. Anat. Rec. 144, 109–116 (1962).
Basmajian, J. Control of individual motor units. Am. J. Phys. Med. 46, 480–486 (1967).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
De Luca, C. J., Donald Gilmore, L., Kuznetsov, M. & Roy, S. H. Filtering the surface EMG signal: movement artifact and baseline noise contamination. J. Biomech. 43, 1573–1579 (2010).
Barachant, A., Bonnet, S., Congedo, M. & Jutten, C. Multiclass brain-computer interface classification by Riemannian geometry. IEEE Trans. Biomed. Eng. 59, 920–928 (2012).
Barachant, A. et al. pyRiemann/pyRiemann: v0.5. (2023).
Williams, A. H. et al. Discovering precise temporal patterns in large-scale neural recordings through robust and interpretable time warping. Neuron 105, 246–259 (2020).
Smith, N. J. & Kutas, M. Regression-based estimation of ERP waveforms: II. Nonlinear effects, overlap correction, and practical considerations. Psychophysiology 52, 169–181 (2015).
Hannun, A., Lee, A. Xu, Q. & Collobert, R. Sequence-to-sequence speech recognition with time-depth separable convolutions. In Proc. Interspeech 3785–3789 (ISCA, 2019)
Karpathy, A. et al. Large-scale video classification with convolutional neural networks. In Proc. 2014 IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2014).
Graves, A., Mohamed, A.-R. & Hinton, G. Speech recognition with deep recurrent neural networks. In Proc. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing 6645–6649 (IEEE, 2013).
Park, D. S. et al. SpecAugment: a simple data augmentation method for automatic speech recognition. In Proc. Interspeech 2613–2617 (ISCA, 2019).
Graves, A., Fernández, S., Gomez, F. & Schmidhuber, J. Connectionist temporal classification: labelling unsegmented sequence data with recurrent neural networks. In Proc. 23rd International Conference on Machine Learning 369–376 (ACM, 2006).
Ney, H., Mergel, D., Noll, A. & Paeseler, A. A data-driven organization of the dynamic programming beam search for continuous speech recognition. In Proc. ICASSP ′87: IEEE International Conference on Acoustics, Speech, and Signal Processing (IEEE, 2005); https://doi.org/10.1109/icassp.1987.1169844.
Rabiner, L. R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE Inst. Electr. Electron. Eng. 77, 257–286 (1989).
Pratap, V. et al. Scaling up online speech recognition using ConvNets. In Proc. Interspeech 2020 (ISCA, 2020); https://doi.org/10.21437/interspeech.2020-2840.
Yang, J., Soh, M., Lieu, V., Weber, D. J. & Erickson, Z. EMGBench: benchmarking out-of-distribution generalization and adaptation for electromyography (2024).
Sultana, A., Ahmed, F. & Alam, M. S. A systematic review on surface electromyography-based classification system for identifying hand and finger movements. Healthc. Anal. 3, 100126 (2023).
Deo, D. R. et al. Brain control of bimanual movement enabled by recurrent neural networks. Sci. Rep. 14, 1598 (2024).
Needleman, S. B. & Wunsch, C. D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 48, 443–453 (1970).
Yu, J. et al. FastEmit: low-latency streaming asr with sequence-level emission regularization. Preprint at arxiv.org/abs/2010.11148 (2020).
Beltagy, I., Peters, M. E. & Cohan, A. Longformer: the long-document transformer. Preprint at arxiv.org/abs/2004.05150 (2020).
Byrd, R. H., Lu, P., Nocedal, J. & Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 16, 1190–1208 (1995).
Olson, B., Hashmi, I., Molloy, K. & Shehu, A. Basin hopping as a general and versatile optimization framework for the characterization of biological macromolecules. Adv. Artif. Intel. 2012, 19 (2012).
Gribble, P. L., Everling, S., Ford, K. & Mattar, A. Hand-eye coordination for rapid pointing movements. Arm movement direction and distance are specified prior to saccade onset: arm movement direction and distance are specified prior to saccade onset. Exp. Brain Res. 145, 372–382 (2002).
Fitts, P. M. The information capacity of the human motor system in controlling the amplitude of movement. J. Exp. Psychol. 47, 381–391 (1954).
MacKenzie, I. S. Fitts’ law as a research and design tool in human-computer interaction. Hum. Comput. Interact. 7, 91–139 (1992).
Fan, J. M. et al. Intention estimation in brain-machine interfaces. J. Neural Eng. 11, 016004 (2014).
MacKenzie, I. S. & Soukoreff, R. W. Phrase sets for evaluating text entry techniques. In Proc. CHI ‘03 Extended Abstracts on Human Factors in Computing Systems—CHI ‘03 754–755 (ACM, 2003); https://doi.org/10.1145/765891.765971.
Gray, H. Anatomy of the Human Body (Lea & Febiger, 1918).
Acknowledgements
We thank S. Druckmann, D. Farina, A. Haith, J. Krakauer, A. Orsborn, C. Pandarinath, L. Paninski, K. Shenoy and D. Wolpert for technical and scientific advice and feedback; and D. Farina, D. Barsakcioglu and P. Rente Vicente for assistance with the wrist MRI scans.
Ethics declarations
Competing interests
All contributors are current or former employees of Meta Platforms, Inc.
Peer review
Peer review information
Nature thanks Cynthia Chestek, Guoying Gu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Schematic and anatomical interfacing of sEMG Research Device.
a, The sEMG Research Device electrical system architecture. The sEMG-RD uses 48 pogo-pin style round electrodes in order to provide good comfort and contact quality. The 48 channels are configured into 16 bipolar channels arranged proximo-distally, with the remainder electrodes serving as either shield or ground. Each electrode is 6.5 mm in diameter (gold plated brass). For each differential sensing channel (16 in total), centre-to-centre spacing between paired sensing electrodes is 20 mm. The sEMG-RD has low noise analog sensors with input-referred RMS noise of 2.46 μVrms, measured during benchtop testing with differential inputs shorted to their mid-point voltage. With analog sensors’ nominal gain value of 190 and Analog to Digital Converter’s (ADC) full-scale range of 2.5 V, the sEMG-RD offers a dynamic range of approximately 65.5 dB. Each channel is sampled at 2000 Hz. The Inertial Measurement Unit (IMU) functional block includes sensors of 3-axis accelerometer, 3-axis gyroscope, and 3-axis magnetometer sampled at 100 Hz. We note that the IMU was not utilized for any online or offline experiments described in this manuscript. The microcontroller facilitates the transfer of unprocessed data from all ADCs and IMU directly to the bluetooth radio. No skin preparation or gels are needed for using the sEMG-RD, because its analog sensors have very high input-impedance — approximately 10 pF capacitance in parallel with 10 TOhm resistance — providing excellent signal robustness against large variations of electrode-skin impedance among the population. b, Computer-aided design rendering of the sEMG-RD. The mechanical architecture consists of a kinematic chain with flexible joints connecting 16 pods that house the pogo-pin style electrodes that comprise the sEMG channels. This enables broad population coverage in maintaining consistent quality contact between the dry electrode and skin. Since each differential sensing channel is placed along the proximal-distal direction, the device is able to maintain symmetry with respect to wrist anatomy and provide generalizability across right and left hands, as long as the wearer keeps the gap location on the ulna side. c, Anatomical depiction of electrode locations relative to relevant muscle and skeletal landmarks, adapted from a public domain image93. Pink overlays cover muscles that predominantly control the wrist, blue overlays cover muscles less involved in wrist control, red overlays cover blood vessels and yellow overlays cover nerves. The green diamond indicates the position of the electrode gap. Note the gap that arises between channels 0 and 15, due to variation in wrist circumference and elasticity between compartments, is aligned with the region of the wrist where the ulna is located.
Extended Data Fig. 2 Extraction and validation of putative MUAPs.
a-b, To evoke putative MUAPs, one participant followed a series of prompts instructing the execution of various low-force muscle contractions interspersed with periods of rest. To facilitate generating sparse and spatially focal EMG signals, the participant was provided visual feedback about the raw EMG on a manually selected channel during prompted rest (a) and movement (b) epochs. Each epoch lasted 10 s and was repeated three times. High-pass EMG on all channels (top) and on the manually selected channel (12) for visual feedback (middle) during a prompted rest epoch during data collection for putative thumb extension MUAPs. Grey vertical scale bars indicate 20 μV. MUAPs on any channel were detected using peak finding on the channel-averaged rectified and smoothed EMG (see Methods). The timings of detected MUAPs were used to construct a spike train capturing the activity of this multi-unit activity, whose instantaneous firing rate was computed by taking the inverse of each event’s interspike interval (ISI) in seconds (bottom). c, Mean instantaneous firing rates (computed as the total number of detected MUAPs over the epoch duration) during rest and movement epochs for each tested movement (IF: index flexion; MF: middle flexion; PE: pinky extension; TAb: thumb abduction; TE: thumb extension; WP: wrist pronation). Each sample corresponds to one prompt (rest or move) epoch. d, Coefficient of variation (CoV) during the prompted movement periods. CoV was computed as the standard deviation of interspike intervals (b; bottom) normalized by their mean. e, Multi-channel waveforms for putative MUAPs extracted during the prompted movement epochs for each action. For visualization, MUAPs for each movement were normalized by the 99.95th percentile of the absolute maximum (over samples and channels) of each MUAP. Thin lines correspond to individual MUAPs (total number detected indicated as n) and thick lines correspond to the median waveform over MUAPs for each movement. Each waveform is 20 ms long. Vertical scale bars indicate 20 uV. f, MUAP spatial profiles. The spatial profile for each MUAP was constructed using the peak-to-peak value of the waveform on each channel. The mean (solid line) and standard error (shading; nearly within solid lines) of the spatial profiles are shown for each movement. Angular locations represent approximate channel locations around the wrist (indicators) and the radii represent the peak-to-peak value.
Extended Data Fig. 3 Anthropometric and demographic features of sEMG datasets.
a, The number of participants in each corpus. b-e, Histograms of anthropometric characteristics of all participants (n = 11,236): (b) wrist circumference, (c) self-reported age, (d) BMI calculated from self-reported height and weight, and (e) self-reported height. The irregularity in the histogram of self-reported age is likely due to participants rounding their age to nearby values. We measured wrist circumferences with a standard measuring tape at the wrist just below the ulnar styloid process where the participants are expected to don the band. Values outside of the range of 10–30 cm were truncated. We calculated BMI as the weight (in kilograms) divided by height (in metres) squared. f-i, Distributions of the demographic characteristics across all participants (n = 11,236): (f) dominant handedness, (g) self-reported proficiency at typing on a computer keyboard, (h) self-reported gender, and (i) arm exercise frequency, chosen from one of the following options: Never (never), Less than once per week (rarely), 1-2 times per week (occasionally), more than twice per week (often).
Extended Data Fig. 4 Examples of prompting used to collect training data for the three tasks.
a, Time series of example prompter frames from the open-loop task used to collect training data for the wrist decoder. The participant was instructed to make wrist movements following a cursor (pink circle) making centre-out movements. For the user to be able to preempt the direction of the cursor movement, a line emanated out from the cursor to indicate the direction it was going to move to before subsequently moving. b, Time series of example prompter frames from the cursor-to-target closed-loop control task used to collect training data for the wrist decoder, with the 2D target configuration. In this task the participant was prompted to move the cursor to a highlighted target (light blue rectangle in panel labelled t0). When the cursor (red) landed on the target, a short timer began, marked by the black fill of the cursor and black border of the target region (panel t3). In this trial, the cursor was held on the target for 500 ms to complete the timer, so the target was acquired and therefore disappeared as the next target was prompted (light blue rectangle in panel t4). c, Example prompter from the smooth pursuit closed-loop control task used to collect training data for the wrist decoder. In this task the participant was instructed to move the cursor (red) to follow a target (black) moving in a randomly sampled smooth trajectory. d, Example of prompting for open-loop task used to collect training data for the discrete gesture recognizer. A series of gestures to be performed are depicted, with colours and labels corresponding to the gesture type. Gestures were separated by blank intervals in which no gesture was to be performed. Prompts scroll from the right of the screen to the left. Participants were instructed to perform each gesture when the corresponding prompt reached the indicator line (highlighted with an arrow) – either instantaneous gestures such as finger pinches or thumb swipes that are depicted as single lines, or held gestures such as index and middle holds that are depicted as solid bars. Participants were instructed to release held gestures when the indicator line reached the end of the rectangle. Gestures that have already been prompted are shown in grey. e, Detailed example of prompting during holds. At t0 an index hold gesture prompt appeared on the right side of the screen, with the time indicator line in white. At t1 the gesture prompt reached the time indicator, and the hold prompt changed colour to indicate the hold should be performed by the participant. At t2 the hold was no longer selected by the indicator bar and turned grey, indicating that the participant should release the hold. f, Example prompter shown during the handwriting task. The screen instructed the participant to write “how was your day” with their hand on the surface of the table, while seated. g, During the experimental session, different prompts, including numbers and punctuation, were shown, ranging from single characters to full sentences. Besides writing on a desk surface, the participant was also asked to perform handwriting on their leg while standing and on their leg while seated.
Extended Data Fig. 5 sEMG event similarities and single-participant sEMG decoder generalization performance.
a, Purple: cosine similarity between individual sEMG activations of a given gesture and the sEMG template (event-triggered average) for that gesture. From left to right: cosine similarities are plotted for all events within a single session (single band placement), across all sessions of a single participant, or across all sessions from all participants from Fig. 2a (100 sessions, 5 from each of 20 users). While similarity was relatively high within a single band placement, sEMG activations became progressively more distinct across different band placements and individuals. Orange: same, except for the cosine similarity of one gesture compared to the template for a distinct gesture. These were lower than similarity within the same gesture, irrespective of whether the grouping was done over a single band placement or across the population. Differences shown across sessions, participants and gestures are representative for all gestures and pairs of gestures. Boxes show median, lower quartile, and upper quartile, with whiskers extending to ±1.5×IQR. b, For each held-out individual, the fraction of other single-participant models in the discrete gesture detection task (Fig. 2c,d) that outperform that individual’s own model (i.e. had lower FNR). For all except two participants, none of the other single-participant models outperformed their own model. All the results in panels b-d are based on n = 100 single-participant models, each trained on 4 sessions from that participant. c, For each pair of participants, we computed the FNR of each participant’s model on data from every other participant. We embedded the resulting distance matrix in 2D using t-SNE. Qualitative inspection of t-SNE embeddings reveal no prominent similarity structure. d, Scatter plot comparing each person’s model’s average offline performance on every other participant’s data (donor FNR, x-axis) against the average performance of other participant’s models on that person’s held-out session (receiver FNR, y-axis). The dashed line shows x = y. There is not a significant Pearson correlation between the donor and receiver score (r = 0.11, p = 0.26, two-sided test, n = 100 participants). All models show high FNR, and the lack of correlation indicates that the generalizability of a given participant’s model to other individuals is not predictive of the other individual’s model’s generalizability to that participant.
Extended Data Fig. 6 Multivariate power frequency features improve wrist decoder performance over root mean square power features.
Decoding error of 4.4 M parameter wrist decoders trained to predict wrist angle velocity from MPF EMG features (black) or root mean square power EMG features (gold). Each dot shows mean +/- SEM decoding error evaluated on a fixed test set of held-out participants (n = 22), following the same conventions as in Fig. 2e. Asterisks below each pair of points indicate p < 10−4, two-tailed paired sample Wilcoxon signed-rank test. Root mean square power EMG features were calculated by first rescaling and high-pass filtering the EMG signal as in the MPF features (see Methods) and then taking the root mean square of each channel in a rolling window of length 200 samples (100 ms) strided by 40 samples (20 ms). The reduced dimensionality of these features (16 dimensions, as opposed to 384) implied a smaller number of input dimensions to the fully connected layer in the rotational-invariance module, which we compensated for by increasing the number of hidden dimensions from 512 to 600 to keep the total parameter count at 4.4 M.
Extended Data Fig. 7 Example screenshots of closed-loop evaluation tasks.
a, Screenshots from an example trial of 1D horizontal cursor control task, in which the participant was prompted to reach to the rightmost target (in panel labelled t0, light blue rectangle). When the cursor (red) landed on the target, the target was marked with a black border and a short timer began, marked by the black fill of the cursor (middle panel, t1). In this trial, the cursor was held on the target for 500 ms to complete the timer, so the target was acquired and therefore disappeared as the next target was prompted (right panel, t2). b, Screenshots from an example sequence in the discrete grid navigation task, in which the participant was prompted to perform (from left to right, marked as t0-t4): thumb swipe up, index hold, thumb swipe right, thumb swipe right, middle hold. c, Screenshots from an example trial in the handwriting task, in which the participant is prompted to write the phrase “example flashing red light means” (top) and the handwriting decoding model output in response to the participant’s behavior in the handwriting task (below).
Extended Data Fig. 8 Additional online evaluation metrics.
a, Mean Fitts’ law throughput on the 1D horizontal cursor control task. Throughput is defined as the index of difficulty divided by acquisition time, with the index of difficulty defined as in5: \({\log }_{2}(1+{d}_{i}/w)\), where \({d}_{i}\) is the distance to the target at the start of trial i and w is the target width. Each box shows the distribution of trial-averaged throughput over participants (n = 17), following the same conventions as Fig. 3d,e. Throughput significantly improved from the practice block to the evaluation blocks (p < 0.005, two-tailed Wilcoxon signed-rank test), indicating learning effects consistent with the improvements in acquisition time and dial-in time shown in the main text. Dashed red line and shading shows median and 95% confidence interval of the performance of a different set of n = 162 participants controlling the cursor with ground truth wrist angles measured via motion capture (see Methods). Dashed orange line and shading shows median and 95% confidence interval of the performance of the same n = 17 participants controlling the cursor with MacBook trackpad (see Methods). For each baseline, confidence intervals for medians were calculated using the reverse percentile bootstrap. b-d, Performance on the discrete grid navigation task with Nintendo Switch Joy-Con controller (n = 23 participants). (b) Fraction of prompted gestures in each block in which the first gesture detected by the model was the correct one (out of 130 total prompted gestures in each block), as in Fig. 3f. This value was used as the baseline in Fig. 3f. (c) Mean gesture completion rate in each task block, as in Fig. 3g. This value was used as the baseline in Fig. 3g. (d) Discrete gesture confusion rates in evaluation blocks, averaged across participants, as in Fig. 3h. Confusion rates are expressed as a percent of instances in which the corresponding gesture was expected (across rows). Note that, despite using a commercially available and widely used controller, confusion rates remain non-zero, reflecting behavioural errors. e, Distribution of subjective impressions about the reliability of each EMG decoding model. At the end of each online evaluation task, participants were asked to respond to a multiple choice question about how reliably their intended action was detected. For the discrete gestures task, they were asked to answer this question separately for each of the thumb swipe directions and “activation” gestures. f-i, Demographics of participants that performed the online evaluation tasks for the wrist decoder (n = 17), discrete gestures decoder (n = 24), and handwriting decoder (n = 20): (f) self-declared gender, (g) self-declared dominant hand, (h) self-declared age, (i) measured wrist circumference. For all boxplots, boxes show median, lower quartile, and upper quartile, with whiskers extending to ±1.5×IQR. Any values beyond these are marked with open circles. One and two asterisks respectively indicate p < 0.05 and p < 0.005, and “ns” indicates “not significant” (p > 0.05); two-tailed paired sample Wilcoxon signed-rank test.
Extended Data Fig. 9 Spatiotemporal properties of all discrete gesture decoder convolutional filters.
a, Index of channel with max root mean square (RMS) power (n = 512 convolutional filters). Here and in all other panels in this figure, the triangles at the top mark the values of the 6 example convolutional filters from Fig. 4b (blue triangles) and the 6 example putative MUAPs from Fig. 4c (orange triangles). b, Number of channels with RMS power within 50% of the peak channel. c, Peak frequency response of the channel with max RMS power. d, Bandwidth of the channel with max RMS power (see Methods).
Extended Data Fig. 10 Influence of early stopping during personalization.
In this figure, we employ early stopping during personalization to disambiguate the role of more personalization data from increased fine-tuning iterations as well as to mitigate regressions among the best-performing users. Specifically, we used mean CER on held out test data as a selection criteria for epoch-wise early stopping. Aside from early stopping, the setup here is identical to that in Fig. 5b,e,f) of the main text. Overall, results are very similar to Fig. 5 of the main text, indicating that the increase in personalization data is the primary driver of improved performance. Regressions among the best-performing users are now absent. Note also that we do not have separate validation and test sets, so these results should be understood as validation performance. a, Same as Fig. 5b of the main text, except with the inclusion of early stopping during fine-tuning. b, Same as Fig. 5e of the main text, except with the inclusion of early stopping during fine-tuning. Compared with Fig. 5e, transfer of personalized models to other participants yields overall smaller regressions likely because early-stopped models remain closer to the pre-trained model. c, Same as Fig. 5f of the main text, except with the inclusion of early stopping during fine-tuning. Regressions exhibited by a few of the best performing users in Fig. 5f are now absent due to early stopping. We show the range of Pearson correlation coefficients for each fit and the median p-value (two-sided test); maximum p-value over all fits is 0.020.
Supplementary information
Supplementary Tables
Supplementary Tables 1 and 2.
Reporting Summary
Supplementary Video 1 Example session of the 1D horizontal cursor control task with generic wrist decoding model.
Example user performing the 1D horizontal cursor control task with the generic wrist decoding model evaluated in Fig. 3d,e. This participant has previous experience with sEMG decoders on this task, but is not in the training or test corpus. In each trial, the participant was prompted to move the cursor to a target and acquire it by holding the cursor within the target region for 500 ms. Once that target is acquired, the target disappears and another is prompted. Once all 10 targets are acquired, another 10 identical targets are presented and prompted in random order. The video shows all 50 trials in one task block, where a trial is defined as a single target acquisition. The video at the bottom right shows the user’s hand during the task. In this block, this user achieved a mean acquisition time of 1.23 s, a mean throughput of 2.26 bits per s, prematurely exited the target on 44% of trials and had a mean dial-in time of 1.07 s on those trials with premature exits.
Supplementary Video 2 Example session of the discrete grid navigation task with a generic discrete-gesture decoding model.
Example user performing the discrete grid navigation task with the generic discrete-gesture decoding model evaluated in Fig. 3f–h. This user has previous experience with sEMG decoders on this task, but is not in the training or test corpus. In each trial, the participant is instructed to move a character along a sequence of points on a grid by using the four navigation gestures (thumb swipe left/right/up/down). Every few steps, a coloured point with text prompts the participant to perform an activation gesture (thumb tap, index hold, middle hold). The video shows all 10 trials in one task block. The video at the bottom right shows the user’s hand during the task. In this block, this user achieved a first hit probability of 0.99, a mean gesture completion rate of 1.31 gestures per s and a mean accuracy (mean of diagonal of the confusion matrix) of 99.2%.
Supplementary Video 3 Example session of the handwriting task with handwriting decoding model.
Example user performing the handwriting task with the generic handwriting decoding model evaluated in Fig. 3i,j. This user has previous experience with sEMG decoders on this task, but is not in the training corpus. In each trial, the participant is prompted to write a phrase. The video shows all 10 trials in one task block. The video at the bottom right shows the user’s hand during the task. In this block, this user achieved a CER of 0.057 and a WPM of 28.4. While we instructed users to make corrections to decoded text that was not understandable, in this particular session, the user did not have to make any such corrections.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kaifosh, P., Reardon, T.R. & CTRL-labs at Reality Labs. A generic non-invasive neuromotor interface for human-computer interaction. Nature 645, 702–711 (2025). https://doi.org/10.1038/s41586-025-09255-w
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s41586-025-09255-w
This article is cited by
-
Brain–computer interface control with artificial intelligence copilots
- Johannes Y. Lee
- Sangjoon Lee
- Jonathan C. Kao
Nature Machine Intelligence (2025)