Interferometric single-shot parity measurement in InAs–Al hybrid devices

To make use of a topological phase for quantum computation, it is crucial to manipulate and measure the topological charge. This can be achieved through protected operations such as braiding and fusing non-Abelian anyons, which offer exponential suppression of errors induced by local noise sources and a discrete set of native operations^15,16,17. Protocols for measurement-only topological quantum computation simplify these operations, reducing them to fusion alone^1,5. This fundamental measurement is sufficient to enact all topologically protected operations. New error-correction schemes have been developed to take advantage of these operations^18,19,20. The robustness against errors and simplicity of control offered by this approach make measurement-based topological qubits a promising path towards utility-scale quantum computation, in which managing the interactions of millions of qubits is necessary^21,22,23,24.

1DTSs^2,3,4 are a promising platform for building topological qubits. Quantum information is stored in the fermion parity of MZMs localized at the ends of superconducting wires and projective measurements of the fermion parity are used to process quantum information and perform qubit-state readout^25,26. The fermion parity shared by a pair of MZMs can be determined through an interferometric measurement^3,6,7,8,9. Several conceptual designs for topological qubits incorporate such interferometers^5,10,11,27. These proposals require time-resolved measurements of the fermion parity in the interference loop, which cannot be accomplished with dc transport measurements of the time-averaged fermion parity²⁸.

In this paper, we demonstrate such a time-resolved measurement, thereby validating a necessary ingredient of topological quantum computation. The measurement technique is based on examining the quantum capacitance C_Q of a quantum dot coupled to the nanowire^5,29,30,31 (Fig. 1) and allows determination of the parity in a single shot. We achieve an assignment error probability of 1% for optimal measurement time. By itself, this measurement does not unequivocally distinguish between MZMs in the topological phase and fine-tuned low-energy Andreev bound states in the trivial phase^{32,33,34,35,36,37,38,39,40} but it does require the low-energy state to be supported at both ends of the wire and very weakly coupled to other low-energy fermionic states. Moreover, it provides a measurement of the state’s energy with single-μeV resolution. These features of the measurement strongly constrain the nature of the low-energy state.

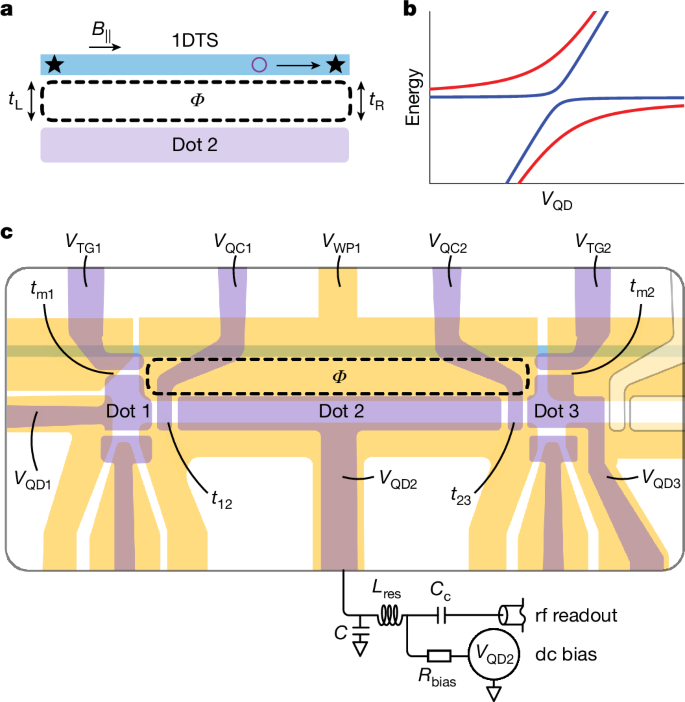
a, Idealized model of the system. A nanowire tuned into a 1DTS state hosts MZMs at its ends, depicted by stars. A quantum dot is tunably coupled to the MZMs by tunnel couplings t_L and t_R, forming an interferometer, which is sensitive to the magnetic flux Φ enclosed by the dashed line and the combined fermion parity Z of the dot–MZMs system. Poisoning by a quasiparticle (purple circle) flips the parity. b, Example energy spectra of the interferometer with total parity Z = −1 (red) and Z = +1 (blue) in the vicinity of the avoided crossing between the states with N and N + 1 electrons on the dot, as a function of the plunger voltage on the quantum dot; see equation (2). c, Gate layout for the interference loop formed by the triple quantum dot and the gate-defined nanowire (light green). Voltage V_WP1 is applied to the wire plunger gate (yellow) and voltage V_QD2 is applied to the dot 2 plunger gate (purple). The effective couplings t_L and t_R of panel a depend on the couplings t_m1, t₁₂ and t_m2, t₂₃ and detuning of quantum dots 1 and 3, respectively. Quantum dot 2 is capacitively coupled to an off-chip resonator chip for dispersive gate sensing and C_Q measurement, which also includes a bias tee for applying dc voltages.

Full size image

We introduce a device architecture enabling projective measurements of fermion parity^{5,10,11,27,29,41,42}. The device comprises two primary components, as illustrated in Fig. 1. The first component is a nanowire that will have MZMs at its ends if it is in a 1DTS state. The second component consists of quantum dots, which are designed to couple pairs of MZMs in an interferometric loop.

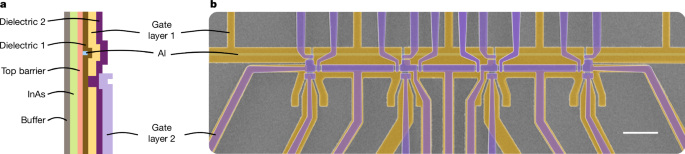
The nanowire in this device is based on a gated superconductor–semiconductor heterostructure and defined by a narrow Al strip that suppresses depletion underneath it^12,13,14. Device fabrication and details of the heterostructure design are discussed in Sections 1.2 and 1.3 of the Supplementary Information, respectively. The Al strip is grounded and continuous throughout, but there are separate ‘plunger’ gates that define five sections of the wire. One of them is shown schematically in Fig. 1c and all five are visible in the scanning electron microscopy image in Fig. 2b. Although there are no breaks in the Al, the plunger gates independently control the density in each section. (See Supplementary Fig. 1 and Section 1.1 of the Supplementary Information for a complete device schematic and gate-naming convention; throughout the paper, V_i refers to the dc voltage applied to gate i.) A topological qubit would require tuning the second and fourth segments, each of length L ≈ 3 μm, into the 1DTS state, whereas the other three would be fully depleted underneath the Al strip (see Supplementary Fig. 1 for details). Here we focus on the second section shown in Fig. 1c and implement a parity measurement using its associated interferometer.

a, Cross-section of the gate-defined superconducting nanowire device design. b, Scanning electron microscopy image with the aluminium strip (blue), first gate layer (yellow) and second gate layer (purple) indicated in false colour. Scale bar, 1 μm.

Full size image

Our readout circuit is based on dispersive gate sensing of a triple quantum dot interferometer (TQDI): three electrostatically defined quantum dots that, together with the second nanowire section, form a loop threaded by a flux, Φ (Fig. 1a,c). We control Φ by varying the out-of-plane magnetic field, B_⊥. The TQDI has two smaller dots (dots 1 and 3), which serve as tunable couplers providing control over, respectively, the tunnel couplings t_L and t_R. The smaller dots are connected to the ends of the 1DTS through tunnel couplings t_mi, in which i = 1, 2, and to the long quantum dot (dot 2) that connects to dot 1 and dot 3 through tunnel couplings t₁₂ and t₂₃, respectively. The quantum capacitance, C_Q, of dot 2 is read out through dispersive gate sensing using an off-chip resonator circuit in a reflectometry setup⁴³; a detailed description is given in Section 1.4 of the Supplementary Information.

We have developed an rf-based quantum dot–MZM tuning protocol that we use to balance the arms of the interferometer. We measure C_Q in a configuration in which one of the small dots is maximally detuned, effectively interrupting the loop. Comparing these measurements with simulations, we extract the couplings t₁₂, t₂₃, t_m1 and t_m2 (see Section 2.5 of the Supplementary Information). This measurement protocol expands on the dc transport techniques proposed in refs. ^44,45 and demonstrated in ref. ⁴⁶. Our rf-based protocol offers μeV-level resolution for coupling extraction, which enables tuning the effective dot-to-wire couplings t_L and t_R. Once we have determined the appropriate voltages for quantum dots 1 and 3, we proceed with interferometry measurements. Section 4 of the Supplementary Information contains further details of the tune-up procedure.

To measure a time record of the fermion parity, we tune up the TQDI and perform a sequence of nearly 1.5 × 10⁴ consecutive measurements of the resonator response, each with an integration time of 4.5 μs, thereby recording a time trace of total length 67 ms. To improve visibility and compare with theoretical predictions, we downsample the time trace by averaging over a 90-μs window. By comparing the measured resonator response with a reference trace (taken with dot 2 in a Coulomb valley), we convert it to a \({\widetilde{C}}_{{\rm{Q}}}\) record, which includes a field-dependent shift of C_Q that cancels out of ΔC_Q (see equation (28) in the Supplementary Information).

We sweep V_QD2 to find charge transitions in dot 2 and, because the normal to the plane of the device is only slightly offset (<1°) from the x axis of the magnet, we sweep the x component of the magnetic field B_x in steps of 0.14 mT to study the dependence on Φ. Our B_x sweep range is offset from 0 so that B_⊥ (which contains a contribution from B_z) is swept symmetrically around 0. We use the topological gap protocol (TGP)¹⁴ to select an in-plane field B_∥ and a wire plunger gate voltage V_WP1 range (indicated, respectively, in Fig. 1a,c) for our measurements, as discussed in Section 4 of the Supplementary Information. The readout system parameters that we achieve are not strongly dependent on these values. For measurement A1 of device A, the relevant regime is B_∥ ≈ 1.8 T and V_WP1 ≈ −1.832 V.

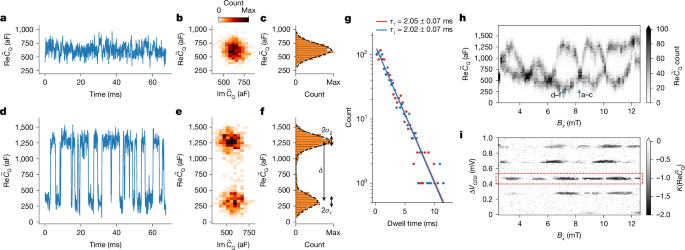
For appropriately tuned quantum dot plungers, in particular for V_QD2 close to resonance, the measured \({\widetilde{C}}_{{\rm{Q}}}\) record exhibits switches between two capacitance values that differ by a ΔC_Q(B_x) that oscillates as a function of B_x. At some B_x, there are no visible switches, as in Fig. 3a, so ΔC_Q(B_x) vanishes. At generic B_x, there is a clear random telegraph signal (RTS), which is shown in Fig. 3d for the B_x that corresponds to maximal ΔC_Q(B_x). From a histogram of all \({\widetilde{C}}_{{\rm{Q}}}\) observed within this time trace, we extract an achieved SNR of 5.01 in 90 μs (Fig. 3e,f) or, equivalently, an SNR of 1 in 3.6 μs (see Section 3.3 of the Supplementary Information). As demonstrated in Fig. 3g, the intervals between switches follow an exponential distribution with a characteristic time τ_RTS ≈ 2 ms. By plotting histograms of the \({\widetilde{C}}_{{\rm{Q}}}\) time traces as a function of B_x, as shown in Fig. 3h, we observe a B_x-dependent bimodal distribution of \({\widetilde{C}}_{{\rm{Q}}}\) values with peaks separated by ΔC_Q(B_x). The oscillation period of ΔC_Q(B_x) is 1.9 ± 0.1 mT, which is consistent with the expected flux of h/2e through the interference loop in this device geometry. We interpret the RTS in C_Q as originating from switches of the fermion parity in the wire; see Section 7.3 of the Supplementary Information for details.

Measurements in device A (measurement A1) in the (B_∥, V_WP1) parameter regime identified through the tune-up procedure discussed in the main text and Section 4 of the Supplementary Information; specifically, V_WP1 = −1.8314 V and B_∥ = 1.8 T. The raw rf signal has been converted to complex \({\widetilde{C}}_{{\rm{Q}}}\) by the method described in Section 3.1 of the Supplementary Information. a,d, Time traces at B_x values corresponding to minimal (panel a) and maximal (panel d) values of ΔC_Q for a fixed choice of V_QD2 close to charge degeneracy. b,e, Histograms of complex \({\widetilde{C}}_{{\rm{Q}}}\) for the time trace shown in panels a and d. c,f, Histograms of the real part \({\rm{Re}}{\widetilde{C}}_{{\rm{Q}}}\) with Gaussian fits for an extraction of the SNR = δ/(σ₁ + σ₂) = 5.01, the details of which are given in Section 3.3 of the Supplementary Information. g, Histogram of dwell times aggregated over all values of B_x, in which the signal shows bimodality. Fitting to an exponential shows that the up and down dwell times agree to within the standard error on the fits: 2.05 ± 0.07 ms and 2.02 ± 0.07 ms, respectively. h, Histogram of \({\widetilde{C}}_{{\rm{Q}}}\) values as a function of B_x, showing clear bimodality that is flux-dependent with period h/2e. The vertical arrows indicate the B_x values at which the time traces in panels a and d were taken. i, Kurtosis in the measured quantum capacitance, \(K(\text{Re}{\widetilde{C}}_{{\rm{Q}}})\), of dot 2 as a function of B_x (which controls Φ) and ΔV_QD2, the change in dot plunger gate voltage from the starting point of the scan (which controls the dot 2 detuning). The dashed red rectangle indicates the ΔV_QD2 value at which the data in the other panels were taken.

Full size image

The visibility and phase of the oscillations vary between successive charge transitions in dot 2. We illustrate this by showing the kurtosis K(C_Q) (which detects bimodality; see Section 3.2 of the Supplementary Information) of the \({\widetilde{C}}_{{\rm{Q}}}\) time traces for several different charge transitions in Fig. 3i. A similar difference in the visibility of flux-induced oscillations across different charge transitions was recently observed in a double quantum dot interferometer experiment⁴⁷. In Section 6 of the Supplementary Information, we discuss oscillations with different periods that are observed at other points in the parameter space of the device.

We support this interpretation by reproducing our results with quantum dynamics simulations that incorporate rf drive power, charge noise and temperature. To build intuition for those simulations, we use an idealized model (see Section 2.2 of the Supplementary Information) subject to the following assumptions (which we will later relax): the wire is in the topological phase and there are no sub-gap states other than the MZMs; the charging energy and level spacing in the dots are much greater than the temperature; dots 1 and 3 are sufficiently detuned that their influence is fully encapsulated in the effective couplings t_L and t_R to MZMs at the ends of the wire (see Fig. 1a); and the drive frequency and power are both negligible. In this limit, the quantum capacitance as a function of the total fermion parity in the quantum dot–wire system, Z, is given by

in which E_D is the detuning from the charge-degeneracy point, α is the lever arm of the plunger gate to the dot, E_M is the MZM energy splitting and T is the temperature. The net effective tunnelling that results from the interference between different trajectories from the dot to the MZMs and back, t_C(Z, ϕ), is

Here ϕ is the phase difference between t_L and t_R, which is controlled by the magnetic flux Φ through the interference loop created by the dot, the wire and the tunnelling paths between them according to ϕ = 2πΦ/Φ₀ + ϕ₀, in which Φ₀ = h/e and ϕ₀ is a flux-independent offset. To capture the extent to which C_Q can be used to discriminate between Z = ±1, it is convenient to introduce

The interferometer must be well balanced t_L ≈ t_R for ΔC_Q to be large according to equation (1). When E_M = 0, ΔC_Q exhibits maxima along the E_D = 0 line, with flux periodicity h/2e.

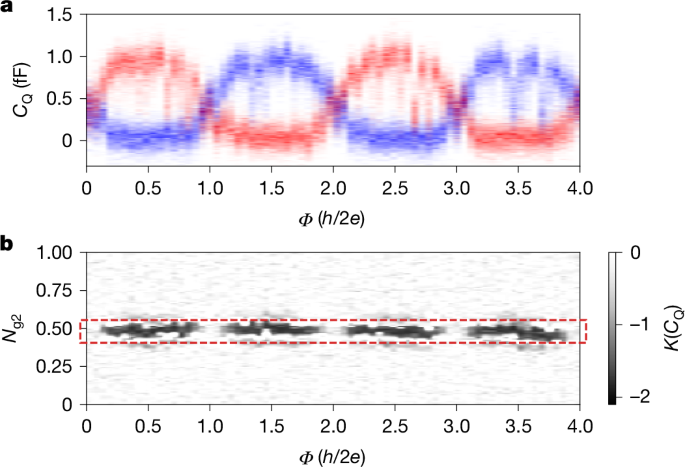
For detailed comparison with experiments, we use the methods discussed in Sections 2.4 and 2.5 of the Supplementary Information to simulate a more complete model of the device and readout chain that includes the full triple-dot system, incoherent coupling to the environment (using parameters inferred from separate measurements; see Sections 9 and 10 of the Supplementary Information) and measurement backaction. Crucially, this approach allows us to incorporate different noise sources in a systematic and quantitative way without any free parameters. The simulated dynamical C_Q, defined in Section 2.3 of the Supplementary Information, is shown in Fig. 4. The C_Q histograms in Fig. 4a reveal two h/e-periodic branches (one shown in red and the other in blue), associated with the two parities of the coupled system. If the fermion parity Z were perfectly conserved, then the device would remain in one of the two parity eigenstates and the Φ dependence would follow either the blue or the red trace in Fig. 4a. However, Z should fluctuate on a timescale given by the quasiparticle poisoning time τ_qpp. Hence, in traces over times longer than τ_qpp, a bimodal distribution of C_Q values is expected, that is, both the blue and red traces in Fig. 4a. Consequently, the kurtosis K(C_Q) exhibits minima at which ΔC_Q is peaked, as shown in Fig. 4b, and time traces taken at these points will exhibit a telegraph signal composed of switches between the values C_Q(1, ϕ) and C_Q(−1, ϕ). Comparing Fig. 4 with Fig. 3h,i, we find good overall agreement of both the histograms and the kurtosis. We find a maximum ΔC_Q(Φ) ≈ 1 fF, which is consistent with our measurements in Fig. 3. This agreement extends to other parameter regimes, such as when the interferometer is poorly balanced or the splitting E_M is sizeable, as discussed in Section 6 of the Supplementary Information.

Simulated dynamical C_Q as a function of magnetic flux and dot 2 gate offset charge N_g2, including the effects of charge and readout noise, as well as non-zero temperature, drive power and frequency, per the discussion in the text. a, Histogram of the two parity sectors for fixed N_g2 = 0.49. Here we used t_m1 = t_m2 = 6 μeV, t₁₂ = t₂₃ = 8 μeV, E_C1 = 140 μeV, E_C2 = 45 μeV, E_C3 = 100 μeV, N_g1 = N_g3 = 0.3, T = 50 mK and E_M = 0. b, Kurtosis of C_Q(t) as a function of N_g2 and flux through the loop. The middle of the dashed red rectangle indicates the N_g2 value used for the linecut in panel a.

Full size image

A second measurement of device A and a measurement of a second device (device B) give results in qualitative agreement with those of measurement A1, demonstrating the reproducibility of the observed phenomena (Section 5 of the Supplementary Information). We have tested our interpretation by: (1) disconnecting the dots from the wire; (2) measuring at fields of 0.8 T below the region identified by TGP; (3) intentionally injecting quasiparticles into the superconductor and observing the effect on τ_RTS; and (4) comparing the quasiparticle density measured in a separate test structure with that inferred according to the hypothesis that τ_qpp = τ_RTS ≈ 2 ms (Section 7 of the Supplementary Information).

By extending the model introduced above, we have analysed the quasi-MZM scenario discussed in previous works^37,38,39,48. We introduce an extra pair of ‘hidden’ Majorana modes that are weakly coupled to each other and to the visible MZMs, which themselves are coupled to quantum dots 1 and 3. Together, the hidden and visible MZMs form a trivial low-energy state at each end of the wire. This scenario can occur in the trivial phase, in which it requires some fine-tuning to make the couplings small. In Section 2.7 of the Supplementary Information, we show that the hidden Majorana modes suppress ΔC_Q owing to fast fermion tunnelling between them and the visible MZMs. This effect completely washes out the flux-dependent bimodality unless the coupling between the ‘hidden’ Majorana modes and the visible MZMs is less than 1 neV or the hidden Majorana modes are effectively gapped out, as shown in Supplementary Fig. 4.

We have presented dispersive gate-sensing measurements of the quantum capacitance in InAs–Al hybrid devices using a system architecture that can be adapted to other materials platforms^49,50. After tuning the nanowire density and in-plane magnetic field into the parameter regime identified by the TGP¹⁴ and balancing the interferometer formed by the nanowire and the quantum dots, we observed a flux-dependent bimodal RTS in the quantum capacitance, which we interpret as switches of the parity of a fermionic state in the wire. We have fit these data to a model in which the fermion parity is associated with two MZMs localized at the opposite ends of a 1DTS and find good agreement. These measurements do not, by themselves, determine whether the low-energy states detected by interferometry are topological. However, our data tightly constrain the allowable energy splittings in models of trivial Andreev states.

In conclusion, our findings represent substantial progress towards the realization of a topological qubit based on measurement-only operations. Single-shot fermion parity measurements are a key requirement for a Majorana-based topological quantum computation architecture.

1. Bonderson, P., Freedman, M. & Nayak, C. Measurement-only topological quantum computation. Phys. Rev. Lett. 101, 010501 (2008).

   ADS  MathSciNet  PubMed  MATH  Google Scholar 

2. Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys.-Usp. 44, 131 (2001).

   ADS  MATH  Google Scholar 

3. Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).

   ADS  PubMed  MATH  Google Scholar 

4. Oreg, Y., Refael, G. & von Oppen, F. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).

   ADS  PubMed  MATH  Google Scholar 

5. Karzig, T. et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 95, 235305 (2017).

   ADS  Google Scholar 

6. Akhmerov, A. R., Nilsson, J. & Beenakker, C. W. J. Electrically detected interferometry of Majorana fermions in a topological insulator. Phys. Rev. Lett. 102, 216404 (2009).

   ADS  CAS  PubMed  MATH  Google Scholar 

7. Fu, L. & Kane, C. L. Probing neutral Majorana fermion edge modes with charge transport. Phys. Rev. Lett. 102, 216403 (2009).

   ADS  PubMed  MATH  Google Scholar 

8. Fu, L. Electron teleportation via Majorana bound states in a mesoscopic superconductor. Phys. Rev. Lett. 104, 056402 (2010).

   ADS  PubMed  Google Scholar 

9. Houzet, M., Meyer, J. S., Badiane, D. M. & Glazman, L. I. Dynamics of Majorana states in a topological Josephson junction. Phys. Rev. Lett. 111, 046401 (2013).

   ADS  PubMed  Google Scholar 

10. Plugge, S. et al. Roadmap to Majorana surface codes. Phys. Rev. B 94, 174514 (2016).

    ADS  MATH  Google Scholar 

11. Vijay, S., Hsieh, T. H. & Fu, L. Majorana fermion surface code for universal quantum computation. Phys. Rev. X 5, 041038 (2015).

    MATH  Google Scholar 

12. Nichele, F. et al. Scaling of Majorana zero-bias conductance peaks. Phys. Rev. Lett. 119, 136803 (2017).

    ADS  PubMed  MATH  Google Scholar 

13. Suominen, H. J. et al. Zero-energy modes from coalescing Andreev states in a two-dimensional semiconductor-superconductor hybrid platform. Phys. Rev. Lett. 119, 176805 (2017).

    ADS  CAS  PubMed  MATH  Google Scholar 

14. Aghaee, M. et al. InAs-Al hybrid devices passing the topological gap protocol. Phys. Rev. B 107, 245423 (2023).

    ADS  CAS  MATH  Google Scholar 

15. Kitaev, A. Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).

    ADS  MathSciNet  CAS  MATH  Google Scholar 

16. Freedman, M. H. P/NP, and the quantum field computer. Proc. Natl Acad. Sci. USA 95, 98–101 (1998).

    ADS  MathSciNet  CAS  PubMed  PubMed Central  MATH  Google Scholar 

17. Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).

    ADS  MathSciNet  CAS  MATH  Google Scholar 

18. Hastings, M. B. & Haah, J. Dynamically generated logical qubits. Quantum 5, 564 (2021).

    MATH  Google Scholar 

19. Paetznick, A. et al. Performance of planar Floquet codes with Majorana-based qubits. PRX Quantum 4, 010310 (2023).

    ADS  Google Scholar 

20. Grans-Samuelsson, L. et al. Improved pairwise measurement-based surface code. Quantum 8, 1429 (2024).

    MATH  Google Scholar 

21. Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).

    ADS  Google Scholar 

22. Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).

    MATH  Google Scholar 

23. Gidney, C. & Ekerå, M. How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. Quantum 5, 433 (2021).

    MATH  Google Scholar 

24. Beverland, M. E. et al. Assessing requirements to scale to practical quantum advantage. Preprint at https://arxiv.org/abs/2211.07629 (2022).

25. Sau, J. D., Clarke, D. J. & Tewari, S. Controlling non-Abelian statistics of Majorana fermions in semiconductor nanowires. Phys. Rev. B 84, 094505 (2011).

    ADS  MATH  Google Scholar 

26. van Heck, B., Akhmerov, A. R., Hassler, F., Burrello, M. & Beenakker, C. W. J. Coulomb-assisted braiding of Majorana fermions in a Josephson junction array. New J. Phys. 14, 035019 (2012).

    MATH  Google Scholar 

27. Fidkowski, L., Lutchyn, R. M., Nayak, C. & Fisher, M. P. A. Majorana zero modes in one-dimensional quantum wires without long-ranged superconducting order. Phys. Rev. B 84, 195436 (2011).

    ADS  Google Scholar 

28. Whiticar, A. M. et al. Coherent transport through a Majorana island in an Aharonov–Bohm interferometer. Nat. Commun. 11, 3212 (2020).

    ADS  CAS  PubMed  PubMed Central  MATH  Google Scholar 

29. Plugge, S., Rasmussen, A., Egger, R. & Flensberg, K. Majorana box qubits. New J. Phys. 19, 012001 (2017).

    ADS  MATH  Google Scholar 

30. Steiner, J. F. & von Oppen, F. Readout of Majorana qubits. Phys. Rev. Res. 2, 033255 (2020).

    CAS  MATH  Google Scholar 

31. Khindanov, A., Pikulin, D. & Karzig, T. Visibility of noisy quantum dot-based measurements of Majorana qubits. SciPost Phys. 10, 127 (2021).

    ADS  MathSciNet  Google Scholar 

32. Janvier, C. et al. Coherent manipulation of Andreev states in superconducting atomic contacts. Science 349, 1199–1202 (2015).

    ADS  CAS  PubMed  MATH  Google Scholar 

33. Hays, M. et al. Direct microwave measurement of Andreev-bound-state dynamics in a semiconductor-nanowire Josephson junction. Phys. Rev. Lett. 121, 047001 (2018).

    ADS  CAS  PubMed  MATH  Google Scholar 

34. Hays, M. et al. Coherent manipulation of an Andreev spin qubit. Science 373, 430–433 (2021).

    ADS  MathSciNet  CAS  PubMed  MATH  Google Scholar 

35. Wesdorp, J. J. et al. Dynamical polarization of the fermion parity in a nanowire Josephson junction. Phys. Rev. Lett. 131, 117001 (2023).

    ADS  CAS  PubMed  MATH  Google Scholar 

36. Elfeky, B. H. et al. Evolution of 4π-periodic supercurrent in the presence of an in-plane magnetic field. ACS Nano 17, 4650–4658 (2023).

    CAS  PubMed  PubMed Central  MATH  Google Scholar 

37. Kells, G., Meidan, D. & Brouwer, P. W. Near-zero-energy end states in topologically trivial spin-orbit coupled superconducting nanowires with a smooth confinement. Phys. Rev. B 86, 100503 (2012).

    ADS  Google Scholar 

38. Liu, C.-X., Sau, J. D., Stanescu, T. D. & Das Sarma, S. Andreev bound states versus Majorana bound states in quantum dot-nanowire-superconductor hybrid structures: trivial versus topological zero-bias conductance peaks. Phys. Rev. B 96, 075161 (2017).

    ADS  MATH  Google Scholar 

39. Vuik, A., Nijholt, B., Akhmerov, A. R. & Wimmer, M. Reproducing topological properties with quasi-Majorana states. SciPost Phys. 7, 061 (2019).

    ADS  MathSciNet  CAS  MATH  Google Scholar 

40. Valentini, M. et al. Nontopological zero-bias peaks in full-shell nanowires induced by flux-tunable Andreev states. Science 373, 82–88 (2021).

    ADS  MathSciNet  CAS  PubMed  MATH  Google Scholar 

41. Vijay, S. & Fu, L. Physical implementation of a Majorana fermion surface code for fault-tolerant quantum computation. Phys. Scr. 2016, 014002 (2016).

    MATH  Google Scholar 

42. Vijay, S. & Fu, L. Teleportation-based quantum information processing with Majorana zero modes. Phys. Rev. B 94, 235446 (2016).

    ADS  Google Scholar 

43. Hornibrook, J. M. et al. Frequency multiplexing for readout of spin qubits. Appl. Phys. Lett. 104, 103108 (2014).

    ADS  MATH  Google Scholar 

44. Clarke, D. J. Experimentally accessible topological quality factor for wires with zero energy modes. Phys. Rev. B 96, 201109 (2017).

    MATH  Google Scholar 

45. Prada, E., Aguado, R. & San-Jose, P. Measuring Majorana nonlocality and spin structure with a quantum dot. Phys. Rev. B 96, 085418 (2017).

    ADS  MATH  Google Scholar 

46. Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).

    ADS  CAS  PubMed  MATH  Google Scholar 

47. Proskoet, C. G. et al. Flux-tunable hybridization in a double quantum dot interferometer. SciPost Phys. 17, 074 (2024).

    MATH  Google Scholar 

48. Prada, E., San-Jose, P. & Aguado, R. Transport spectroscopy of NS nanowire junctions with Majorana fermions. Phys. Rev. B 86, 180503 (2012).

    ADS  MATH  Google Scholar 

49. Bonderson, P., Nayak, C., Reilly, D., Young, A. F. & Zaletel, M. Scalable designs for topological quantum computation. U.S. patent 11,751,493 B2 (2023).

50. ten Haaf, S. L. D. et al. A two-site Kitaev chain in a two-dimensional electron gas. Nature 630, 329–334 (2024).

    ADS  PubMed  MATH  Google Scholar 

51. Microsoft (United States). Interferometric single-shot parity measurement in InAs-Al hybrid devices. Zenodo https://doi.org/10.5281/zenodo.14804379 (2025).

Download references

Authors and Affiliations

1. Microsoft Azure Quantum, Redmond, WA, USA

   Morteza Aghaee, Alejandro Alcaraz Ramirez, Zulfi Alam, Rizwan Ali, Mariusz Andrzejczuk, Andrey Antipov, Mikhail Astafev, Amin Barzegar, Bela Bauer, Jonathan Becker, Umesh Kumar Bhaskar, Alex Bocharov, Srini Boddapati, David Bohn, Jouri Bommer, Leo Bourdet, Arnaud Bousquet, Samuel Boutin, Lucas Casparis, Benjamin J. Chapman, Sohail Chatoor, Anna Wulff Christensen, Cassandra Chua, Patrick Codd, William Cole, Paul Cooper, Fabiano Corsetti, Ajuan Cui, Paolo Dalpasso, Juan Pablo Dehollain, Gijs de Lange, Michiel de Moor, Andreas Ekefjärd, Tareq El Dandachi, Juan Carlos Estrada Saldaña, Saeed Fallahi, Luca Galletti, Geoff Gardner, Deshan Govender, Flavio Griggio, Ruben Grigoryan, Sebastian Grijalva, Sergei Gronin, Jan Gukelberger, Marzie Hamdast, Firas Hamze, Esben Bork Hansen, Sebastian Heedt, Zahra Heidarnia, Jesús Herranz Zamorano, Samantha Ho, Laurens Holgaard, John Hornibrook, Jinnapat Indrapiromkul, Henrik Ingerslev, Lovro Ivancevic, Thomas Jensen, Jaspreet Jhoja, Jeffrey Jones, Konstantin V. Kalashnikov, Ray Kallaher, Rachpon Kalra, Farhad Karimi, Torsten Karzig, Evelyn King, Maren Elisabeth Kloster, Christina Knapp, Dariusz Kocon, Jonne V. Koski, Pasi Kostamo, Mahesh Kumar, Tom Laeven, Thorvald Larsen, Jason Lee, Kyunghoon Lee, Grant Leum, Kongyi Li, Tyler Lindemann, Matthew Looij, Julie Love, Marijn Lucas, Roman Lutchyn, Morten Hannibal Madsen, Nash Madulid, Albert Malmros, Michael Manfra, Devashish Mantri, Signe Brynold Markussen, Esteban Martinez, Marco Mattila, Robert McNeil, Antonio B. Mei, Ryan V. Mishmash, Gopakumar Mohandas, Christian Mollgaard, Trevor Morgan, George Moussa, Chetan Nayak, Jens Hedegaard Nielsen, Jens Munk Nielsen, William Hvidtfelt Padkar Nielsen, Bas Nijholt, Mike Nystrom, Eoin O’Farrell, Thomas Ohki, Keita Otani, Brian Paquelet Wütz, Sebastian Pauka, Karl Petersson, Luca Petit, Dima Pikulin, Guen Prawiroatmodjo, Frank Preiss, Eduardo Puchol Morejon, Mohana Rajpalke, Craig Ranta, Katrine Rasmussen, David Razmadze, Outi Reentila, David J. Reilly, Yuan Ren, Ken Reneris, Richard Rouse, Ivan Sadovskyy, Lauri Sainiemi, Irene Sanlorenzo, Emma Schmidgall, Cristina Sfiligoj, Mustafeez Bashir Shah, Kevin Simoes, Shilpi Singh, Sarat Sinha, Thomas Soerensen, Patrick Sohr, Tomas Stankevic, Lieuwe Stek, Eric Stuppard, Henri Suominen, Judith Suter, Sam Teicher, Nivetha Thiyagarajah, Raj Tholapi, Mason Thomas, Emily Toomey, Josh Tracy, Michelle Turley, Shivendra Upadhyay, Ivan Urban, Kevin Van Hoogdalem, David J. Van Woerkom, Dmitrii V. Viazmitinov, Dominik Vogel, John Watson, Alex Webster, Joseph Weston, Georg W. Winkler, Di Xu, Chung Kai Yang, Emrah Yucelen, Roland Zeisel, Guoji Zheng & Justin Zilke

Consortia

Microsoft Azure Quantum

Contributions

The Microsoft Azure Quantum team conceived the technology reported in this article and designed, fabricated and operated the device and system reported here. All authors wrote and revised the manuscript and the Supplementary Information.

Corresponding author

Correspondence to Chetan Nayak.

Competing interests

The authors declare no competing interests.

Peer review information

Nature thanks Hao Zhang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions