Humans learn generalizable representations through efficient coding

Introduction

The aphorism “A man can never step into the same river twice” speaks to the ever-changing nature of the world. Making sense of this dynamic reality requires the ability to generalize; that is, to extract knowledge from past experiences and apply it to new, unseen futures. Effective generalization remarkably improves the capacity of intelligent agents to adapt to rapid changes. For example, consider a child learning to ride a bike. She makes numerous attempts, falling and adjusting her balance through trial and error. Once bike riding is mastered, the child can then generalize those balancing skills to ride a scooter, allowing her to quickly master the scooter without having to learn from scratch. Given its importance to adaptive learning, generalization has been the focus of study in both cognitive neuroscience^1,2,3 and machine learning^4,5,6.

Recent research illustrates that representation learning is one of the cornerstones that support generalization^7,8,9. Representation learning involves the transformation of raw environmental stimuli or events into robust abstract states (“state abstraction”), which summarize underlying patterns and regularities in the raw data. For example, riding a bike and scooter may be conceptually abstracted into one activity, enabling a child to realize they can transfer balancing skills previously learned from riding a bicycle to a scooter. In addition, effective representations can detect and extract a subset of the most informative and rewarding features within environments (“rewarding feature extraction”). For instance, although bicycles and scooters have distinct designs, their shared feature of having two wheels requires similar balancing skills. Historically, there has been a gap in the theoretical and comprehensive understanding of how to constitute effective representations. Bridging this gap and developing algorithms that learn generalizable representations has become a central pursuit in recent research on human cognitive neuroscience^9,10,11,12 and artificial intelligence^{7,13,14,15,16}.

This paper focuses on understanding how humans learn effective representations that enhance their generalization abilities. One influential framework for understanding human behavioral learning is reinforcement learning (RL), which views intelligent behavior as seeking to maximize expected reward^17,18. This framework provides a normative understanding of a spectrum of human learning processes^{19,20,21,22,23,24,25,26} and offers theories on the underlying neural mechanisms^27,28,29,30. However, by itself, the traditional RL framework provides very limited insights into human representation learning and generalization^{10,20,31,32,33}. The framework often assumes a predefined, fixed set of task representations on which learning can operate directly, without the need for additional representation learning¹⁷. However, in real-world decision-making, humans are not provided with predefined representations. Instead, they must infer these representations from complex and dynamic environmental observations.

Here, we propose augmenting the classical RL theory to incorporate the principle of efficient coding³⁴: while maximizing reward, intelligent agents should use the simplest necessary representations. The origin of this approach lies in the basic fact that the human brain, as a biological information processing system, possesses finite cognitive resources³⁵. The idea of efficient use of cognitive resources has had profound impacts across many domains in psychology and neuroscience, including perception^36,37,38, working memory^39,40, perceptual-based generalization³, and motor control⁴¹. Furthermore, our approach aligns with Botvinick’s⁴² proposal that the efficient coding principle can be instrumental in understanding the representation of problems in learning and decision-making. Our work extends their proposal by concretely operationalizing efficient coding using information theory, providing a calculable measure within the RL framework, and validating this idea on human data.

Critically, our proposed approach suggests that, driven by the principle of efficient coding, an intelligent agent can autonomously learn appropriate simplified representations, which enables both state abstraction and the extraction of rewarding features, naturally resulting in generalization. To validate these predictions, we designed two experiments focusing on learning and generalization. Participants first learned a set of stimulus-action associations and were then tested on their ability to generalize to a new set of associations they had not encountered before. The first experiment investigates the emergence of state abstraction, while the second explores the extraction of rewarding features. Human participants displayed strong generalization abilities in both experiments, correctly responding to new associations without additional training. We developed a principled model based on efficient coding and demonstrated its capacity to achieve human-level generalization performance in both experiments—performance that classical RL models have not accomplished. These findings lead us to conclude that generalization is an inherent outcome of efficient coding. Given humans’ remarkable capacity for generalization, we assert that the classical RL objective augmented with efficient coding and reward maximization presents a more comprehensive computational objective for human learning.

Results

Humans exhibit two types of generalizations: perceptual-based and functional-based generalizations. Perceptual-based generalization occurs when two stimuli share a similar appearance^1,38,39. Functional-based generalization, in contrast, occurs between stimuli that have similar functions (e.g. linked to the same actions), even when they do not look alike^{2,43,44,45,46}. The latter type of generalization is more complex because it necessitates the acquisition of unseen environmental statistics before it can occur.

To investigate both types of generalization, we leveraged the acquired equivalence paradigm^2,43,44. This experimental framework first links two visually distinct stimuli with identical actions, then assesses the increase in generalization between these stimuli based on their shared actions. This approach effectively establishes the functional similarity between the two stimuli, enabling a controlled experimental investigation into participants’ ability of functional-based generalization.

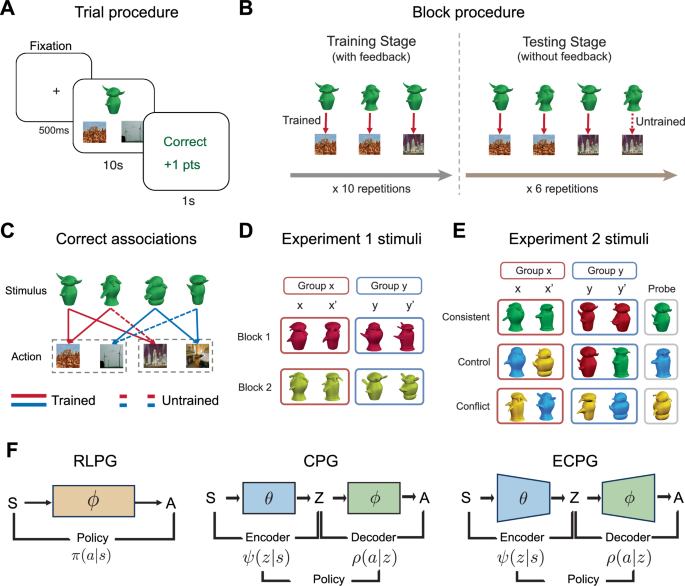
Specifically, participants performed a two-stage task. In each trial, participants were shown an alien (stimulus $s$) and were told that different aliens preferred to visit different locations. For a given stimulus, participants were required to choose one of two places (action $a$) that they believed the alien would prefer to visit (Fig. 1A). During the training stage, participants were trained on six stimulus-action associations, each repeated ten times to learn the equivalence between stimuli based on their associated actions (Figs. 1B and 1C). For example, if aliens s₁ and s₂ both preferred to visit a desert (a₁) rather than a forest (a₂), then they are equivalent and the psychological similarity of the two aliens may increase. During the training stage, participants received feedback (reward $r$, taking a value of either 0 or 1) after every choice.

**Fig. 1: Acquired equivalence experimental paradigm and model architectures.**

In the testing stage, participants were tested on eight associations: the six trained associations plus two untrained associations that were not presented in the training stage. The untrained associations were used to evaluate people’s generalization performance. For example, if the participant learned during the training stage that ${s}_{1}$ and ${s}_{2}$ were similar to each other (had similar preferences), then participants might generalize other preferences from ${s}_{1}$ to ${s}_{2}$, even though no feedback was given about those preferences. No feedback was provided during the testing stage, and each association was repeated six times.

To quantify human generalization ability, we calculate the “untrained accuracy”, which is the response accuracy for the untrained associations that were not presented during training. The higher the untrained accuracy, the better a participant’s generalization ability. Similarly, “trained accuracy”—the response accuracy for trained associations that were presented in the training stage—serves as a measure of human learning performance. Both metrics are crucial and will be used extensively throughout this paper.

All data were collected online via Amazon Mechanical Turk.

Modeling human behavior at the computational level

David Marr⁴⁷ famously argued that the human brain can be understood at three levels: the computational level, which defines the goals to be achieved; the algorithmic level, which details the specific algorithms the human brain used to reach these goals; and the implementational level, which describes how these algorithms are physically realized. In psychology and cognitive science, researchers often build models at the algorithmic level. They typically postulate specific cognitive mechanisms within the human brain, describe these mechanisms using computer programs, and demonstrate their explanatory power over human behavioral data^45,46,48.

However, the question of whether the human brain reconstructs efficient representations for task stimuli is situated at the computational level. Therefore, we need to construct models at this same level. In concrete, we formalized our hypotheses—with or without efficient coding—as distinct computational goals, each addressed using the simplest possible algorithm. Unlike algorithmic-level models, computational-level models do not presume specific mechanisms; Instead, these mechanisms naturally emerge during the process of achieving the defined computational goal. Thus, computational-level models not only explain human behaviors but also shed light on the potential cognitive mechanisms underlying these behaviors, thereby demonstrating superior explanatory power over algorithmic-level models.

We built three computational-level models. First, we established a classical RL baseline, named Reinforcement Learning Policy Gradient (RLPG; see Fig. 1F and “Method-Models-RLPG”), which assumes that humans do not learn simplified representations. The computational goal is formulated as follows:

$$\max_\pi {E}_{\pi }\left[r\left({s}_{t},{a}_{t}\right)-b\right]$$

(1)

where $\pi ({a|s})$ is a policy that maps a stimulus, $s$, to a distribution of actions, $a$. On each trial, an agent had to choose between two possible actions, each with a 50% chance of being correct. Prior to making a decision, the agent was expected to have a baseline reward expectation of $b$ = 0.5. This baseline was used to evaluate the “goodness” of the actual reward received. A reward was considered positive if it exceeded the agent’s expectation, otherwise negative. The RLPG model interpreted human behavior as involving the search for the policy that yielded the greatest reward (above the baseline) in the process of interacting with the environment.

Second, we developed an Efficient Coding Policy Gradient model (ECPG; Fig. 1F and “Method-Models-ECPG”), which posits that humans learn simpler representations through efficient coding. The challenge in modeling this principle lies in defining the complexity (or simplicity) of representations. Recent studies on human perception have conceptualized perception as an information transmission process, where an encoder transmits environmental sensory signals ($s$) into internal representation ($z$)^3,39,40. These studies measure the complexity of representations by the amount of information transmitted by the encoder, quantified by the mutual information between stimuli and representations ${I}^{\psi }({S;Z})$. Based on these works, the computational goal of efficient coding is formalized as maximizing reward while minimizing the representation complexity,

$${\max}_{\psi,\rho}{E}_{\psi,\rho }\left[r\left({s}_{t},{a}_{t}\right)-b\right]\,-\lambda {I}^{\psi }\left({S;Z}\right)$$

(2)

The critical parameter $\lambda \ge 0$, referred to as the simplicity parameter, controls for the tradeoff between the classical RL objective and representation simplicity. When $\lambda$ = 0, the agent does not compress stimuli representations for simplicity, and the efficient coding goal reduces to the RL goal. Conversely, as $\lambda \to \infty$, the agent learns the simplest set of representations, encoding all stimuli into a single, identical representation. Therefore, the optimal $\lambda$ should be a moderate value, balancing compressing without oversimplification. Due to the introduction of latent representation $z$, the policy needs to be broken down into an encoder, $\psi$, and a decoder, $\rho$, which are simultaneously optimized according to Eq. 2 (Fig. 1F).

To test whether humans learn compact representations, the establishment of the RLPG and ECPG models would typically be sufficient, because the contrasting hypotheses they represent (RLPG stands for “No”, ECPG stands for “Yes”) together cover the entire hypothesis space. One concern, however, is that the introduction of the representation in ECPG has changed the model architecture, potentially introducing confounding factors. To control these confounders, we implemented a third model, Cascade Policy Gradient (CPG; “Method-Models-CPG”), which also supports the non-efficient coding hypothesis. The CPG is a special case of the ECPG model which sets the simplicity parameters to 0 ($\lambda$ = 0 in Eq. 2) (Fig. 1F),

$${\max}_{\psi,\rho} {E}_{\psi,\rho }\left[r\left({s}_{t},{a}_{t}\right)-b\right]$$

(3)

This model serves as an intermediary between the RLPG and ECPG models, optimizing for the classical RL objective while concurrently updating the representations.

To ensure that observed behavioral differences result only from optimizing different computational goals, we carefully controlled for all other model components. First, all three models address their computational goals using the same policy gradient approach, where models explicitly learn and maintain a parameterized policy^17,49. The method was selected over the more commonly used value function approach in psychology and neuroscience because it introduces a minimum number of parameters, therefore better distilling the computational essence of each computational goal. Second, the three models were initialized to (nearly) the same state. Due to the distinct appearances of stimuli in the experiments, we pretrained the encoders of the CPG and ECPG models to achieve a 99% initial discrimination accuracy among the four stimuli (see “Method-Pretrain an encoder”). We chose a threshold of 99% instead of 100% for two reasons: first, to model the perceptual noise present in the human visual system, and second, to prevent gradient vanishing, which is an engineering concern. The RLPG model implicitly assumes perfect discrimination between stimuli and, therefore, does not require the same pretraining as others. Lastly, we used the same model fitting method for all three models, fitting the parameters to each participant separately using maximum-a-posteriori (MAP) estimation (“Method-Model fitting”), based on behavioral data from both the training and the testing stages.

In the following sections, we demonstrate that, at the computational level, only the ECPG model—which incorporates representation simplification—can qualitatively account for human generalization behaviors. We also compare the ECPG model to several published algorithmic-level models and show that, even without presuming any specific algorithmic details about cognitive mechanisms, the ECPG model surpasses models with handcrafted cognitive mechanisms in describing human behavior. Overall, our findings show that integrating efficient coding into the classical RL objective provides a more comprehensive computational framework for understanding human learning and generalization.

Abstract states inevitably merge in simplified representations, resulting in generalization

Experiment 1 studies human generalization using the standard acquired equivalence paradigm. In this setting, the four alien stimuli within each block share the same color but differ in shapes and appendages (Fig. 1D). This design allows us to specifically study functional-based generalization, because the perceptual features (color, shape, and appendage) provide no cues for generalization.

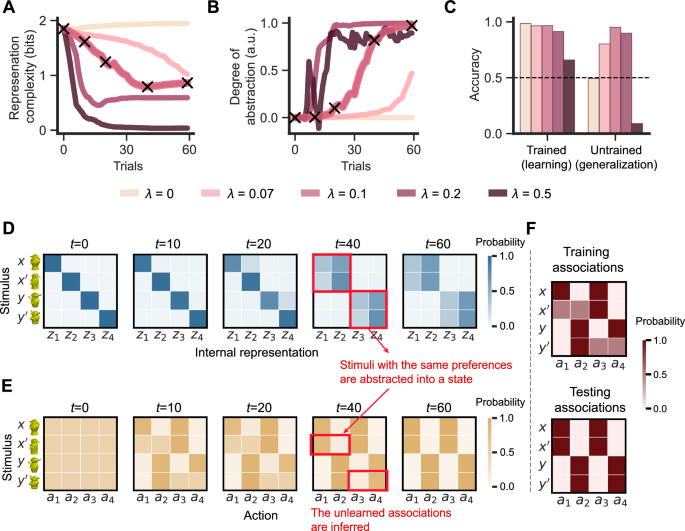
Why can humans generalize? The proposed efficient coding principle posits that, to achieve simplified representations, an agent must appropriately abstract environmental stimuli into robust latent states. Within each of these abstract states, the stimuli can then mutually generalize. To illustrate this, we simulated the ECPG model at different levels of simplicity, controlled by the parameter λ (0, 0.07, 0.1, 0.2, 0.5), while keeping other parameters constant (See simulation details in “Method-Simulation”). Note that when $\lambda$ = 0, the ECPG model reduces to the CPG model, which does not employ efficient coding.

The simulations first demonstrate that efficient coding drives state abstraction. As shown in Fig. 2A ($\lambda$ = 0.1), representation complexity decreases significantly from the beginning of training (t = 0) to the end (t = 60). This representation simplification significantly affects the model’s internal representations ($\lambda$ = 0.1). Before training, when representations are complex, each stimulus is encoded in an unstructured way, with a one-to-one correspondence in representation space (Fig. 2D, t = 0). Driven by efficient coding, the ECPG model compresses representations, discarding redundant information and mapping stimuli associated with the same actions into similar representations, forming abstract states (Fig. 2D, t > 20, red arrows). We quantify the degree of the state abstraction using the Silhouette score⁵⁰, which measures an object’s ($x$) similarity to its own latent state ($x^{\prime}$) relative to other states ($y$ and $y^{\prime}$). A score close to 0 indicates poor abstraction, while a score close to 1 indicates strong abstraction—stimuli within each abstract state ($x$ and $x^{\prime}$) are encoded similarly and associate with each other, while stimuli across abstract states ($x$ and $y$) remain distinct. Figure 2B ($\lambda$ = 0.1) shows the Silhouette score increasing from 0 toward 1, indicating emergence of stable, meaningful abstract states from the initially unstructured set of representations. The stimuli shared the same preferences became associated with each other.

**Fig. 2: The internal dynamics of the ECPG model during training.**

We further show that stimuli within the same abstract state can generalize to each other. After abstract states stabilize (t > 40), the model begins to decode policies from the structured representations, and changes in representation complexity become more nuanced (Fig. 2A, $\lambda$ = 0.1). Policies decoded from stimuli within the same abstract state are similar (Fig. 2E, red arrows), illustrating the ECPG model’s ability to generalize from training to testing associations. This is reflected by the model’s significantly above-chance untrained accuracy (Fig. 2C, $\lambda$ = 0.1), despite being exposed to only a subset of the associations during training (Fig. 2F). Similar results can be observed when $\lambda$ is set to 0.2 (Supplementary Note 1.2).

Note that the degree of state abstraction is critical; both insufficient and excessive abstraction impair generalization. As $\lambda$ increases, the model prioritizes representation simplification over reward maximization, resulting in more intense and rapid abstraction (Fig. 2A). For lower $\lambda$ (0 or 0.07), the ECPG model becomes more reward-focused and exhibits little or no reduction in representation complexity (Fig. 2A, $\lambda$ = 0.07 and 0). The insufficient compression prevents the model from associating stimuli that share the same actions, leading to a failure in state abstraction (Fig. 2B, $\lambda$ = 0.07 and 0) and, consequently, compromised generalization performance (Fig. 2C, $\lambda$ = 0.07 and 0). Conversely, overly compressed representations (Fig. 2A, $\lambda$ = 0.5) tend to oversimplify abstraction, assigning all stimuli to a single internal state. This results in significant reward loss and unstable state abstraction, as reflected by the oscillating Silhouette score (Fig. 2B, $\lambda$ = 0.5). Such oversimplified abstraction can be detrimental to both generalization and learning performance (Fig. 2C, $\lambda$ = 0.5).

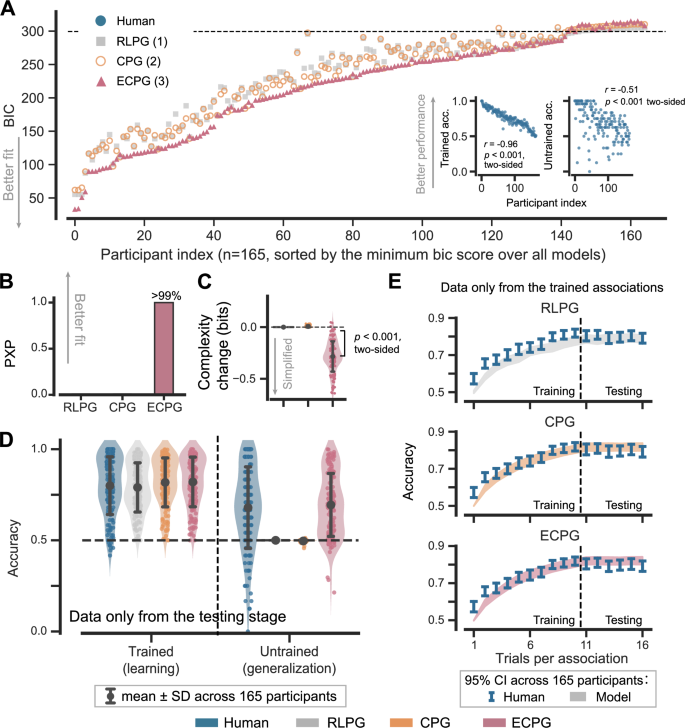
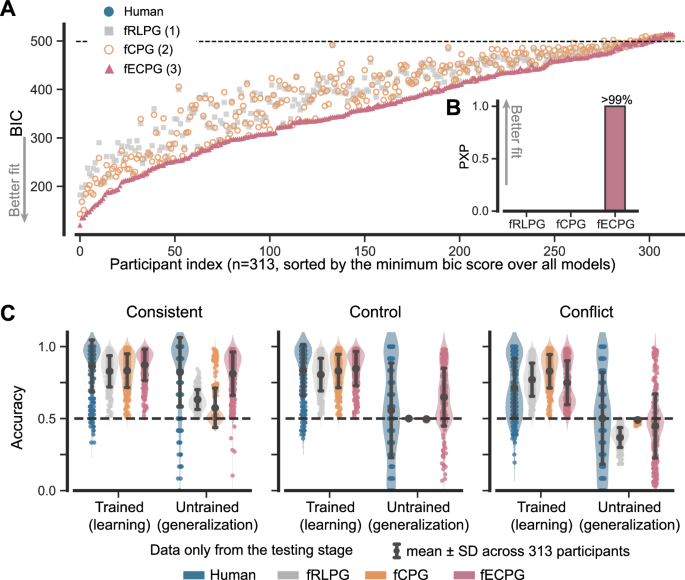
So far, our theoretical framework has outlined how efficient coding could result in functional-based generalization. To verify whether these principles in humans, we collected behavioral data from 165 participants performing two blocks of the standard acquired equivalence task. We fitted all three models to the data and evaluated them using the Bayesian Information Criterion (BIC). The ECPG model best described the majority of participants (Fig. 3A), with a stronger advantage in the testing stage, where generalization occurs (Table 1). Some participants’ behaviors were poorly captured by the ECPG model, primarily due to their low effort, which resulted in poor learning (Pearson’s r(165) = −0.96, p < 0.001, 95% CI = [−0.97, −0.94]) and generalization performance (Pearson’s r(165) = −0.52, p < 0.001, 95% CI = [−0.63, −0.40]). We also conducted a Bayesian group-level comparison and reported the protected exceedance probability (PXP)—the probability that a model accounts for the data better than the others, beyond the chance level (the log model evidence was estimated using the BIC)⁵¹. As expected, the ECPG model again was ranked first among the three models (PXP > 0.999; Fig. 1B). These findings underscore the unique capability of the ECPG model in capturing human learning and generalization performance.

**Fig. 3: Behaviors of humans and models in Experiment 1.**

Table 1 Model Fitting in Experiment 1

Full size table

To show that only the ECPG model learns simplified representations, we computed the change in representation complexity during training, which was quantified as the difference in the mutual information ${I}^{\psi }({S;Z})$ before and after training (Fig. 3C). The ECPG model successfully reduced complexity, indicating that it learned simplified representations as expected. In contrast, the two control models did not compress their representations. Furthermore, we examined the simplicity parameter $\lambda$ of the ECPG model and found it to be significantly greater than 0 (two-sided t(164) = 4.29, p < 0.001, Cohen’s d = 0.33, 95% CI = [0.11, 0.29]) (see Supplementary Note 1.1 for model parameters). This finding suggests that the representation simplification plays an important role in capturing human behaviors.

Human participants generalized effectively. Despite receiving no training, the untrained accuracy for human participants is significantly greater than the 50% chance level, though slightly lower than trained accuracy (Fig. 3D, blue). This observation, consistent with many prior studies^2,43,44, indicates that human participants effectively generalized from prior learning. The ECPG model closely captures this generalization phenomenon, whereas the two control models cannot generalize at all, with the untrained accuracy remaining at the 50% chance level (Fig. 3D, gray and orange). More importantly, the ECPG model’s strong performance in capturing human generalization did not compromise its explanatory power for human learning behavior. It offers a description as precise as that of the two control models concerning the human learning curve throughout the training stage (Fig. 3E).

Based on both quantitative and qualitative evidence, we conclude that humans’ ability to generalize originates from their computational goal of efficient coding. This process promotes the emergence of abstract latent states, which form the foundational basis for generalization.

Efficient coding automatically extracts rewarding features throughout learning simplified representations

Experiment 2 extended the standard paradigm to examine both functional-based and perceptual-based generalizations in humans. The experiment featured two primary modifications. First, we manipulated the stimuli’s perceptual cues--shape, color, and appendage--to ensure each feature provided a different amount of information about the environment’s rewards. We designed three experimental conditions, each with a distinct rewarding configuration (Fig. 1E):

In the consistent condition, the alien stimuli with the same color were associated with the same actions, making the color the most rewarding feature.
In the control condition, the colors of the stimuli were mutually different, and all features were equally rewarding. This condition, like Experiment 1, only tested the functional-based generalization and the state abstraction ability of an agent.
In the conflict condition, stimuli with the same color were associated with different actions, making shapes and appendages the rewarding features, while the color cue yielded a negative reward.

These three conditions also indicated three levels of difficulty in rewarding feature extraction. In the consistent and conflict condition, the four stimuli shared two colors, making color cues more frequent and salient. For example, while the “cylinder” shape was associated with rewards twice during training, the color “red” might have been rewarded four times. The consistent condition was the easiest because this salient feature yielded positive rewards, while the conflict condition was the most difficult because the agent needed to first suppress the color cue, the salient feature, before being able to detect rewarding ones.

The second primary modification in Experiment 2 was the incorporation of a probe stimulus during the testing stage; this stimulus was entirely new and had not been encountered during training. This probe was used to assess humans’ ability to extract informative and rewarding features at a behavioral level. A more detailed introduction to the use of this probe design follows below, along with the presentation of our model’s predictions. All other aspects of the experiment remained identical to those in Experiment 1.

We reused the three models in Experiment 1, only adding a feature embedding function to encode perceptual information. Each of the three visual features was encoded into a five-dimensional one-hot code, where each dimension indicated a specific feature value. For example, the shape “cylinder” was [1, 0, 0, 0, 0], the color “purple” was [1, 0, 0, 0, 0], and the color “yellow” was [0, 1, 0, 0, 0]. Each stimulus was represented by a combination of three such codes, concatenated into a 15-dimensional vector to form the model’s input. We refer to the models used in Experiment 2 as feature RLPG (fRLPG; “Method-Models-fRLPG”), feature CPG (fCPG; “Method-Models-fCPG”), and feature ECPG (fECPG; “Method-Models-fECPG”) models to highlight their integration of the feature embedding construct.

To evaluate the model’s feature extraction ability, we analyzed the importance assigned to each feature by perturbing one feature dimension and measuring changes in representations^52,53. A larger change in the representations indicated a higher feature importance (see “Method-Perturbation-based feature importance”). Therefore, in this experiment, if a model consistently assigns more importance to the predefined rewarding perceptual cue across all three conditions, we conclude that this model can effectively detect and extract rewarding features.

Now that the stage is set, we can focus on answering three central research questions. First, does the principle of efficient coding drive a model to extract rewarding features? Second, if so, how can we validate that humans follow this principle in their learning processes? Third, how does the rewarding feature extraction interact with the state abstraction ability examined in Experiment 1?

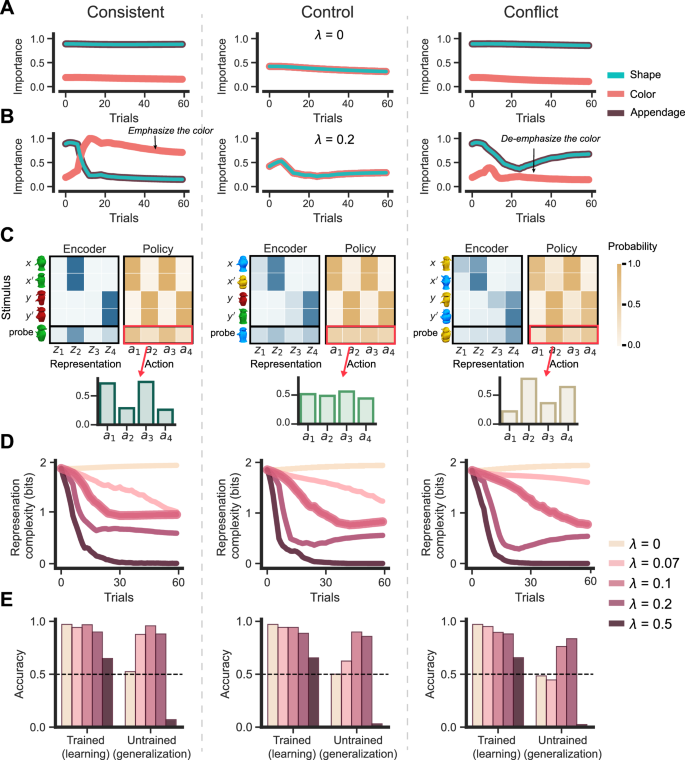
For the first question, we ran stimulations and showed that efficient coding does promote reward feature extraction. As designed in the experiment, color served as the rewarding feature in the consistent condition, while it yielded negative rewards in the conflict condition. Driven by the need for simpler representations—reflected in a focus on fewer features—the fECPG model ($\lambda$ = 0.2) must selectively assign more importance to the color cue in the consistent case; and less importance when the color becomes unrewarding (Fig. 4B, consistent). Conversely, in the conflict condition, the model had to first deemphasize the salient cue color, due to its negative rewards, and then reallocate importance to the other features contributing to positive rewards (Fig. 4B, conflict). The demand for simplicity drives the model to focus on a subset of features, and the goal of maximizing reward ensures that these focused features must be rewarding. In contrast, a model without efficient coding ($\lambda=0$) cannot adaptively reallocate feature importance during its interaction with the environment. The model exhibits nearly the same feature importance assignment for both consistent and conflict cases (Fig. 4A), indicating its inability to detect rewarding information. It is worth noting that the fECPG model unintuitively predicts that shape and appendage are rewarding features before training. We believe this is caused by our simplistic approach to encoder initialization. We will further elaborate this point in the discussion section. However, this observation does not undermine our conclusion.

**Fig. 4: Predictions of the fECPG model in Experiment 2.**

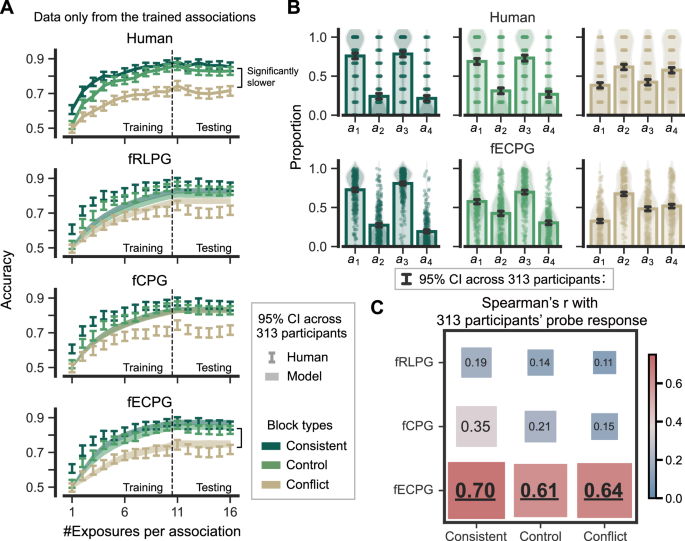
To address the second question, we adopted a “probe” design. The probe stimulus, introduced only during the testing stage and not present in the training, was designed to always share the same color as stimulus $x$ and the same shape as stimulus $y^{\prime}$. In the consistent condition, where color was the most important feature, the probe stimulus should be perceived as similar to stimulus $x$ (Fig. 4C, consistent, encoder), leading to a response that coincides with the one for stimulus $x$ (Fig. 4C, consistent, policy). In this scenario, it is expected that human participants will demonstrate a higher preference for actions ${a}_{1}$ and ${a}_{3}$ when responding to the probe stimuli. Conversely, in the conflict condition where color was neglected, the probe stimulus should be perceived as more similar to stimulus $y^{\prime}$ (Fig. 4C, conflict, encoder), which should be also reflected in the response (Fig. 4C, conflict, policy). Therefore, human participants would be likely to use ${a}_{2}$ and ${a}_{4}$. In the control condition, given the lack of a dominant rewarding feature, the response to the probe stimulus should not show a strong preference, being distributed between those for stimuli $x$ and $y^{\prime}$ (Fig. 4C, control, policy).

For the third question, we observed that the efficiency of rewarding feature extraction extends or shortens the time it takes to form stable abstract states, influencing the agent’s learning and generalization. In the consistent condition, the fECPG model rapidly identified the rewarding feature and formed stable abstract states (Fig. 4D, consistent), enabling a high degree of generalization (Fig. 4E, consistent). However, in the control condition, where no salient cue dominates, the model experienced a slower state abstraction process (Fig. 4D, control). In the conflict condition, the need to suppress color prolonged the time required to extract rewarding features, thereby further extending the state abstraction period (Fig. 4D, conflict). Consequently, the time available for policy decoding was reduced, resulting in poorer learning and generalization performance in the conflict case (Fig. 4E, control, conflict).

To validate these model predictions, we collected behavioral data from 313 participants who each completed three task blocks corresponding to consistent, control, and conflict conditions. We fit all three feature-based models and found that both BIC and PXP preferred the fECPG model as the best model for capturing human behavioral data, consistent with the findings from Experiment 1 (Fig. 5A, B and Table 2).

**Fig. 5: Behaviors of human participants and models in Experiment 2 (part 1).**

Table 2 Model Fitting in Experiment 2

Full size table

More importantly, as the principle of efficient coding predicts, human participants exhibit different levels of generalization across experimental conditions. They achieved high untrained accuracy in the consistent condition, lower in the control condition, and lowest in the conflict condition (Fig. 5C, blue). Beyond the overall trend, humans’ generalization behaviors are also characterized by high variability. Some participants generalized effectively across all conditions, while others always negatively transferred their knowledge. This variability is also accurately captured by the fECPG model (Fig. 5C, red), but not by the two classical RL models without efficient coding (Fig. 5C, gray and orange).

To our surprise, the ECPG model shows a significant advantage in predicting human learning performance—an area where classical RL models have traditionally been preferred. Participants demonstrated a more rapid improvement in the consistent condition than in the control and conflict conditions. Specifically, the learning curve in the conflict condition was markedly slower when compared to the other conditions. Only the fECPG model captured the significantly slower trend (Fig. 6A).

**Fig. 6: Behaviors of human participants and models in Experiment 2 (part 2).**

The probe design further validated the human participant’s ability to extract rewarding features as predicted by the efficient coding principle. Human participants’ responses to the probe stimuli were consistent with the fECPG model predictions (Fig. 6B, C; Spearman’s r > 0.60, p < 0.001 for all conditions; see “Method-Correlation between humans’ and models’ probe response” for the correlation calculation). In contrast, models without efficient coding, fRLPG and fCPG, failed to replicate such behavioral patterns (see Supplementary Note 1.5 for their probe responses), exhibiting significantly weaker correlations with human behavioral data (Fig. 6C).

It is important to note that there is a discrepancy between our prediction and human behavior in the control condition. Human participants were likely to use the policy of stimulus $x$ rather than a random policy in response to the probe. This phenomenon could have arisen from two potential factors. First, during training, the experiment might not have adequately balanced the presentation frequency of the stimuli. Participants learned two associations with stimulus $x$ and one with stimulus $y^{\prime}$ (with the other association tested in the testing stage), which implies that stimulus $x$ was shown twice as frequently as was stimulus $y^{\prime}$. Consequently, participants might have adaptively adjusted their encoding and decision-making on these statistics and placed more attention on stimulus $x$. Second, the color feature might have been inherently more salient to humans. When the three features were equally informative, participants may have naturally prioritized the color feature. However, this gap does not undermine our conclusion that the fECPG model best captures human participants’ responses to the probe stimulus.

All evidence leads to one conclusion: during learning, humans strive to distill representations into their simplest and most essential forms. Driven by this goal, humans learn representations using a small subset of rewarding features within their environments. They further simplify these representations by abstracting them into compact, lower-dimensional internal states, which naturally leads to generalization.

The human brain optimizes efficient coding to enhance learning and generalization

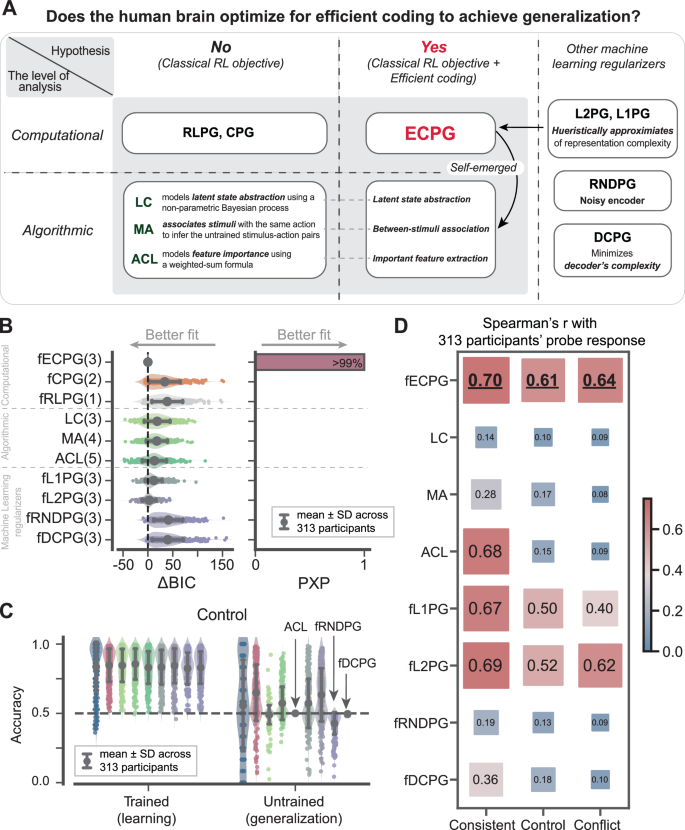
A potential argument is that the classical RL objective is still sufficient to explain human behavior once it is augmented with cognitive mechanisms at the algorithmic level. We oppose this view for two reasons. First, a range of current algorithmic-level models fail to capture human behaviors as effectively as the ECPG model (as detailed below). Second, the mechanisms embedded in these models inherently simplify representations, essentially pursuing efficient coding.

We developed and compared three algorithmic-level models (Fig. 7A). The first model, the Latent Cause model^45,46,54,55 (LC; “Method-Models-LC”) employs a hierarchical nonparametric Bayesian process to simulate human state abstraction. During the learning period, the LC model categorizes observed stimuli into latent clusters and learns the decision policy for these clusters. The second model, called the Memory-Association model (MA; “Method-Models-MA”), memorizes all stimuli and their preferred actions, establishing associations between stimuli that share the same actions. These associations facilitate the inference of correct actions in untrained tasks, thereby enabling generalization. The third model, Attention at Choice and Learning^48,56,57 (ACL; “Method-Models-ACL”) learns the value of each feature and calculates the feature importance based on these values. The model uses a linearly weighted feature value for decision-making. Notably, the LC and MA models emphasize state abstraction ability, whereas the ACL model is designed to extract and prioritize rewarding features. Both abilities could emerge by optimizing for the efficient coding goal, but in a different computational formulation.

**Fig. 7: Comparison of the (f)ECPG model with other algorithmic-level models in Experiment 2.**

We tested these algorithmic-level models on Experiment 2, with a focus on two qualitative metrics: generalization in the control case to examine their latent cause abstraction ability (Fig. 7C) and response to probe stimuli to evaluate their rewarding feature extraction (Fig. 7D). All three models underperformed the fECPG model in terms of BIC and PXP (Fig. 7B, Table 2). The LC and MA models failed to account for human responses to probe stimuli (Fig. 7D) due to lacking feature extraction mechanism. The ACL model struggled with generalizing in the control case (Fig. 7C) as well as extracting rewarding features in both the control and conflict cases (Fig. 7D), because its feature importance calculations cannot deemphasize the negatively-rewarded feature effectively (see Supplementary Note 3.2 for further discussion). These results underscore the superior performance of the fECPG model, a computational-level model, in modeling human behaviors and support our hypothesis that human participants learn simplified representations when maximizing rewards.

From a machine learning perspective, the fECPG model proposed here defines a regularized optimization objective. This raises a final question: can the efficient-coding term be substituted by other commonly used machine learning regularizers? We implemented an L1-Norm Policy Gradient (L1PG; “Method-Models-L1PG, L2PG, and DCPG”) and an L2-Norm Policy Gradient (L2PG), incorporating L1 or L2 norms as heuristic approximations for representation complexity. While the L1PG model underperformed, the L2PG model showed comparable performance to fECPG (Fig. 7B, C, and D). Although a substantial portion ( ~ 36%) of participants were better described by the L2PG model, these participants displayed distinct behavioral dynamics: compared to participants better captured by the fECPG model, they tended to learn more slowly and showed weaker generalization (see Supplementary Note 3.3 for further details). This suggests that the ECPG model has a unique capability in capturing humans’ fast learning and strong generalization patterns. For completeness, we also tested a Random Regularizer Policy Gradient (RNDPG; “Method-Models-RNDPG”), which injects noise into the encoder weights⁵⁸, as well as a Decoder Complexity Policy Gradient (DCPG), which constrains decoder complexity. However, both models failed to generalize in the control condition or extracting rewarding features (Fig. 7B, C, D).

Finally, we validated our conclusions by performing a model recovery analysis to test our ability to differentiate between models (Supplementary Note 1.6). Importantly, we found that the ECPG model can be uniquely distinguished from the other models. The low false positive rate (with other models unlikely to be misidentified as ECPG) indicates that the ECPG model’s superior performance over the control models is not due to its expressiveness but to its accurate description of human behavior. Thus, these findings support our conclusion that the ECPG model, with its efficient coding-augmented RL objective, best accounts for human learning and generalization.

Discussion

The classical RL framework has limitations in terms of its ability to explain human representation learning and generalization. In this paper, we proposed augmenting the classical RL objective with the efficient coding principle: an intelligent agent should distill the simplest necessary representations that enable it to achieve its behavioral objectives. A computational-level model derived from the revised framework (Efficient Coding Policy Gradient; ECPG), predicts that an intelligent agent automatically learns to construct representations with a small set of rewarding features with the environment. These representations are further simplified by abstracting them into compact, lower-dimensional internal states, which naturally results in generalization. These predictions were validated in two behavioral experiments, where the ECPG model consistently provided a more accurate description of human behavior than two classical RL models without efficient coding as well as several published human representation learning models. These findings indicate that efficient coding offers a more suitable computational objective in understanding human behavior.

In this paper, we examine whether the classical RL objective alone, or in combination with efficient coding, better aligns with Marr’s computational level in explaining human behavior. A potential critique of our approach in section “The human brain optimizes efficient coding to enhance learning and generalization” is the lack of comparison with an alternative model capable of generalizing without representation simplification. However, we found no such model in the existing literature. This absence reflects the historical context of the acquired equivalence paradigm on which our study builds. Although generalization within this paradigm has long been documented⁵⁹, previous explanations—including categorization⁶⁰, stimulus association², and selective attention⁶¹—are all encompassed by our efficient coding framework. In other words, algorithmic models based on selective attention, for example, inherently implement mechanisms predicted by the computational-level goal of efficient coding.

Previous research using the acquired equivalence paradigm has demonstrated that people with schizophrenia^62,63, mild Alzheimer’s disease⁶⁴, hippocampal atrophy⁴³, and Parkinson’s disease⁴³ exhibit dysfunction in performing acquired equivalence task. Despite these findings, the neurocognitive mechanisms underlying these impairments remain incomplete understanding. The ECPG model, which provides a detailed computational representation of human learning and generalization within this paradigm, may offer a framework for investigating the cognitive and neural processes underlying these cognitive anomalies. However, this potential application of the ECPG model remains untested and requires empirical validation through experimental studies.

Beyond serving as a better empirical model for human learning, the proposed computational objective could potentially represent a rational strategy (specifically, a resource-rational strategy; see below) for humans. The classical RL objective was designed to maximize expected reward in narrowly defined settings, where agents focus on learning a single, well-defined task¹⁷. However, humans live in more complex and dynamic real-world environments, where decision-making requires agents to generalize effectively from past experiences to earn rewards in unseen scenarios. Moreover, the human brain is innately capacity-constrained³⁵; it has inherent limitations in processing and storing information, which requires the efficient use of cognitive resources. Therefore, learning simpler representations that facilitate generalization is a crucial component in the pursuit of maximizing reward in real-world decision-making. We believe that this insight can also improve learning and generalization in artificial intelligence operating under real-world conditions.

The idea of linking RL to efficient coding has been applied to understand learning and generalization in various contexts^{22,42,65,66,67,68,69}. For example, this approach has been shown to better explain monkeys’ neural activity in frontal areas⁶⁵, humans’ risky choice behavior⁶⁷, and meta-level generalization between tasks⁶⁶. Here, we present a specific formalization of efficient coding using information-theoretic measures. We demonstrate that this approach provides a better empirical description of both human learning and generalization behaviors compared to several alternatives.

Our study also helps bridge the gap between representation learning in the human brain and machine learning. In cognitive science, researchers have applied latent cause clustering (LC) and Association-Choice Learning (ACL) models to understand a variety of phenomena⁹. Latent cause clustering can explain Pavlovian conditioning and extinction⁵⁵, memory modification⁵⁴, social classification⁷⁰, and functional-based generalization^45,46,71. Selective attention, on the other hand, has been used to explain concept formation⁷², the evolution of beliefs⁷³, and has received neural evidence from eye-tracking and functional Magnetic Resonance Imaging (fMRI) studies^48,56. In machine learning, researchers have focused on how information-theoretic regularizers facilitate an artificial agent performing complex cognitive tasks. For example, information-theoretic regularizers may help an agent learn robust state abstractions that enhance learning speed^74,75,76 and form a simple but informative world model^77,78. Our study demonstrates that in a simple cognitive task, both mechanisms serve the unified objective of minimizing representation complexity, guided by an information-theoretic regularizer. This finding facilitates communication between the two fields and contributes to a unified research framework for understanding both machine and human intelligence. Building on this line of thought, we plan to extend the current framework in future research to more complex task settings, such as multi-step Markov Decision Processes (MDPs), and explore whether complex human behaviors like planning and multi-task learning align with the predictions of information-theoretic regularizers within machine learning.

Recent research has suggested that human intelligence is more accurately described by the principle of resource-rationality^79,80 than by the classical notion of rationality⁸¹. The resource-rationality principle emphasizes the need to consider computational costs in the pursuit of maximum reward, building on the classical notion of rationality. The combination of efficient coding and reward maximization principles applied in this study encapsulates the idea of resource-rationality, with reward maximization representing the notion of rationality and representation complexity representing computational costs. The basic idea is that information transmission in the brain incurs significant metabolic costs, thus minimizing representation complexity (a quantification of average information transmitted into the brain) serves as a reasonable proxy to minimize computational costs⁸². Notably, while numerous studies have employed resource-rationality to explain deviations from pure rationality in human behavior^38,83,84, our research further emphasizes the advantages conferred by the principle, particularly in accounting for state abstraction, rewarding feature extraction, and generalization.

Methods

Ethics statement

Participants gave informed consent. The experimental protocol was approved by the University Committee on Activities involving Human Subjects at Rensselaer Polytechnic Institute (IRB-2055). Our experiment did not collect any demographical information from participants, including gender.

Materials

The experiments were designed based on the paradigm of acquired equivalence (AE)^2,43,44. The experiment included two types of pictures: alien and scene. For the alien pictures, we utilized the “greebles” stimuli reported by Gauthier and Tarr^85,86 (http://www.tarrlab.org/). The original greeble stimuli are purple. We created several new variants by modifying their color. Regarding the scene pictures, we sampled from the “Places205” picture database, as reported in Zhou et al.⁸⁷ (http://places.csail.mit.edu/downloadData.html).

In the main experiment blocks, aliens and scenes were organized into sets. Each set comprised four alien stimuli ($x$, $x^{\prime}$, $y$, $y^{\prime}$) and four scenes (${a}_{1}$, ${a}_{2}$, ${a}_{3}$, ${a}_{4}$), resulting in eight unique associations per set. Six of these associations were trained during the association stage, while all eight were tested in the testing stage. It is important to note that the stimuli in the AE task are defined to be “superficially dissimilar”. In our experiment, the greeble stimuli within a block were required to have the same color but exhibit mutually different shapes and appendages. There was no correlation between the alien’s shape (the configuration of its appendages) and the correct response.

Experiments

Experiment 1

We recruited 302 participants from Amazon Mechanical Turk (MTurk)⁸⁸. No statistical method was used to predetermine sample size. All participants gave informed consent before starting the experiment. Each participant completed two practice blocks. To ensure a comprehensive understanding of the experiment, participants were required to achieve at least 70% accuracy in the second practice block to progress to the main experimental stage. Those who did not meet this criterion were allowed to repeat the second practice block until they achieved the necessary performance level; otherwise, they could not proceed to the main experiment. Participants received a base payment of $2 plus a bonus of up to $3 based on their response accuracy in this 20-minute experiment.

This project aimed to study generalization within the learning process, meaning participants who did not learn were outside the scope of this study. Consequently, we excluded 137 participants who failed a screening criterion (average accuracy lower than 60% for the last 24 trials, equating to 4 repetitions, in the training stage). All analyzes in Experiment 1 were conducted with the remaining 165 qualified participants.

The experiment consisted of two types of trials: training and testing. Each training trial comprised three screens. Following a 500 ms fixation screen, the trial presented an alien stimulus in the upper middle of the screen, along with photographs of scenes, offering one correct and one incorrect choice. Participants were instructed, “Which scene is associated with this alien?” and asked to respond by pressing the “F” or “J” key. These choices’ left-right order was counterbalanced across trials. The stimulus screen remained visible for ten seconds, followed by a one-second feedback screen displaying either “Correct! You got 1 point.” or “Incorrect! You got 0 point”. The test stage trials were identical, except that no feedback was provided after responses. In the testing stage, the experiment was directed to the next fixation screen following the participant’s response or after a maximum duration of ten seconds.

Experiment 1 included two experimental blocks. Each block consisted of a training stage, during which participants learned the stimulus-action associations, and a testing stage, during which participants were tested on the learned associations as well as an untrained generalization probe (the dashed associations). The training stage involved each association being trained ten times with feedback, resulting in 6 (associations) × 10 (repetitions) = 60 training trials. The testing stage tested both the trained and untrained associations six times, resulting in 8 (associations) × 6 (repetitions) = 48 testing trials. Participants were explicitly informed of the transition between the two experimental stages, and they were also reminded to keep and reapply their training experiences to achieve better performance.

Before the main blocks, each participant was required to complete two practice blocks. The first practice block contained a simple trial-and-error learning task, where participants were trained to learn the correct answer through feedback. They were asked to correctly associate $x-{a}_{1}$ and $y-{a}_{2}$ without being asked to build any between-stimuli equivalence. This block provided a gentle introduction to the experiment, with ten trials and unlimited response time. The primary goal of the first practice was to familiarize participants with the trial-and-error training process. The second practice served as a quiz. This block included a simplified version of the main training stage, where participants were presented with four stimuli but only required to choose from two actions. It contained 4 (associations) × 10 (repetitions) = 40 training trials. Participants needed to achieve 70% accuracy to pass the quiz; otherwise, they were required to repeat the second practice block before progressing to the main experimental blocks. The practice blocks were designed to help participants learn to establish between-stimuli equivalence in preparation for the main experimental blocks and used similar materials as the main blocks.

Experiment 2

We recruited 497 participants from MTurk. No statistical method was used to predetermine sample size. All participants gave informed consent prior to the experiment. Each participant completed two practice blocks. To ensure full understanding of the experiment, they needed to achieve at least 70% accuracy in the second practice block to proceed to the main experimental stage. Those who did not meet this criterion were given the opportunity to repeat the second practice block until they reached the required accuracy. All participants received a $3 base payment plus up to a $4.5 bonus based on their response accuracy in this 30-minute experiment.

We filtered the participants’ data using the same screening criterion as in Experiment 1. A total of 184 participants were excluded because they did not achieve an average accuracy of 60% for the last 24 trials (equivalent to 4 repetitions) in the training stage. All analyzes in Experiment 2 were conducted with the remaining 313 qualified participants.

Note that Experiment 2 included twice as many qualified participants as Experiment 1. This is because each participant in Experiment 1 completed two identical experimental blocks, while in Experiment 2, participants completed three different blocks, each corresponding to a different experimental condition. To ensure that each condition in Experiment 2 had a comparable amount of data to Experiment 1, we increased participant enrollment.

After completing the same practice blocks as in Experiment 1, participants were required to complete three main experimental blocks: a consistent block, a control block, and a conflict block. The sequence of these blocks was counterbalanced among participants. The three blocks were almost identical; the only difference lay in the stimuli’s appearance.

Within each block, participants were required to complete a 60-trial training stage, which was the same as in Experiment 1. They then entered the testing stage, where they had to respond to eight regular testing associations plus an additional probe stimulus. Consequently, the testing stage comprised 9 (associations) × 6 (repetitions) = 54 trials.

The remaining details of Experiment 2 were identical to Experiment 1. Note that, unlike the untrained associations, we did not predefine a correct answer for the probe stimulus. We simply record participants’ responses and hope to uncover which feature people were attending to by analyzing the response distribution.

Models

To set the stage, we first formalize a dynamic decision process in the AE paradigm. For consistency, we adopt a notation system similar to that used in the experimental paradigm.

We refer to a participant or decision maker as an agent. In each trial $t$, an agent is presented with an alien stimulus ${s}_{t}$ from the set $\{x,\,{x}^{{\prime} },{y},{y}^{\prime} \}$. The agent’s task is to select an action, specifically a scene picture ${a}_{t}$, from the set $\{{a}_{1},\,{a}_{2},\,{a}_{3},\,{a}_{4}\}$, with the objective of maximizing the reward $r({s}_{t},{a}_{t})$ based on the feedback received. The subscript $t$ denotes the variable at a particular trial. Both the stimulus $S$ and action $A$ are defined as categorical variables.

RLPG: reinforcement learning policy gradient

RLPG is a computational level model. The goal of the RLPG model is to identify a policy $\pi$ that optimizes the classical RL goal.

$${{\max }_{\pi }}{{E}_\pi} \left[r\left({s}_{t},{a}_{t}\right)\right]$$

(4)

In the AE experiment, an agent was required to choose from two possible actions; before receiving any feedback, each action had a 50% chance of being correct. The agent should have had a baseline estimation of reward, denoted as $b$, prior to making a decision. An action is considered positive when it yields a reward higher than the baseline and negative when the reward is lower. We revised Eq. 4 to include this baseline reward estimation $b$,

$${{\max }_{\pi }} \, {{E}_{\pi }}\left[r\left({s}_{t},{a}_{t}\right)-b\right]$$

(5)

The formula indicates that the RL baseline learns to adjust the policy π(a|s) to maximize received reward subtracted by the baseline r(s_t,a_t)-b. The reward subtracted by the baseline is commonly called advantage in the machine learning community. In this AE task, we assumed $b$ = 0.5, corresponding to an expected reward of 0.5 (reward of 1 with 50% probability).

The objective function can theoretically be tackled by any RL algorithm, but we have chosen a particular approach for its simplicity: the policy gradient method. We assume the policy follows a parameterized softmax distribution, transforming the optimization problem into a parameter search:

$$\pi \left(a | {s;}\phi \right)=\frac{\exp \left[\phi \left(s,a\right)\right]}{{\sum }_{{a}^{{\prime} }}\exp \left[\phi \left(s,{a}^{{\prime} }\right)\right]}$$

(6)

where $\phi$ denotes the parameters of the policy. Here, $\phi$ is a 4-by-4 table (4 stimuli by 4 action). See Supplementary Note 2.1 for a graphical illustration of the model architecture. For simplicity, we will denote this softmax formula as ${{{\rm{softmax}}}}(\phi (s,a)).$

Let $J\left(\phi \right)={\max }_{\phi }E\left[r\left({s}_{t},{a}_{t}\right)-b\right]$, then the policy parameters were updated based on the gradient of the objective function ${\nabla }_{\phi }J(\phi )$,

$$\phi \left(s,a\right)=\phi \left(s,a\right)+{\alpha }_{\pi }{\nabla }_{\phi } \, J\left(\phi \right)\left(s,a\right)$$

(7)

where ${\alpha }_{\pi }\ge 0$ is the learning rate of policy $\pi$. This policy learning rate is the only parameter in the RL baseline model. The policy parameters $\phi$ were initialized to 0 before the experiment. Equation 7 updates the policy via its gradient, which gives the name “policy gradient”. We have derived the analytical gradient for both models and verified the derivation using pyTorch package⁸⁹. See supplementary material for detailed derivation. The RLPG model features a single parameter: the policy’s learning rate, ${\alpha }_{\pi }$.

There are two remarks related to this simple model. First, though not explicitly shown, the RLPG assumes a perfect representation that fully reconstructs the stimulus. If we construct a model that explicitly includes the representation $z$ and assume that each stimulus $s$ deterministically maps to a unique representation $z$, the model nevertheless collapses to the RLPG model described above. Second, the RLPG model introduced in this study behaves similarly to the classic Q-learning model which is extensively used in psychology²⁵. The most significant advantage of RLPG is its simplicity. The model has a single learning rate parameter, simultaneously approximating the effects of both the “learning rate” and “inverse temperature” parameters in the classic model. This allows for a more effective distillation of the computational essence underlying representation compression.

ECPG: efficient coding policy gradient

The ECPG model is designed with a dual computational goal: to maximize reward while minimizing representation complexity.

$${{\max }_{\psi,\rho }} \, {E}_{\psi,\rho }\left[r\left({s}_{t},{a}_{t}\right)-b\right]-\lambda {I}^{\psi }\left({S;Z}\right)$$

(8)

The parameter $\lambda \ge 0$, referred to as the simplicity parameter, controls for the tradeoff between the classical RL objective and representation simplicity. When $\lambda=0$, the agent does not compress stimuli representations for simplicity, focusing solely on reward maximization. Conversely, as $\lambda \to \infty$, the agent learns the simplest set of representations, encoding all stimuli into a single, identical representation. Therefore, an optimal $\lambda$ balances compression and oversimplification.

The introduction of latent representation $z$ divides the policy into an encoder, $\psi$, and a decoder, $\rho$, both of which are optimized according to Eq. 8. Like the RLPG, we solve Eq. 8 using the policy gradient. Here, we considered a parameterized softmax encoder $\psi ({z|s;}\theta )$ and a decoder ρ(a│z;ϕ). The encoder parameter θ is a 4-by-4 table (4 stimuli by 4 representations) and the decoder parameter $\phi$ is also a 4-by-4 table (See Supplementary Note 2.3.3 for a graphical illustration of the model architecture). The policy $\pi$ is derived from the combination of the encoder and decoder:

$$\pi \left({a}_{t} | {s}_{t}\right)={\sum }_{z}\phi \left(z | {s}_{t};\theta \right)\rho \left({a}_{t} | {z;}\phi \right)$$

(9)

We iteratively update the encoder and decoder to optimize Eq. 8 using the following scheme:

$$\left\{\begin{array}{c}{\max }_{\theta }J\left(\theta \right)={\max }_{\theta } {\sum} _{z}\psi \left(z | {s}_{t};\theta \right)\left[\rho \left({a}_{t} | z\right)\left(r\left({s}_{t} ; {a}_{t}\right)-b\right)-\lambda \log \frac{\psi \left(z | {s}_{t};\theta \right)}{p\left(z\right)}\,\right]\\ {\max }_{\phi }J\left(\phi \right)={\max }_{\phi }{\sum} _{z}\rho \left({a}_{t} | {z;}\phi \right)\left[\psi \left(z | {s}_{t}\right)\left(r\left({s}_{t},{a}_{t}\right)-b\right)\right] \hfill \\ p\left(z\right)={\sum} _{s}\psi \left(z | s\right)p\left(s\right) \hfill \end{array}\right.$$

(10)

Here, $p(z)$ indicates the prior preference to the representation $z$. The first two optimization problems were solved using gradient ascent with learning rate parameters, ${\alpha }_{\psi }$ and ${\alpha }_{\rho }$. The prior representation probability $p(z)$ was updated according to the definition of marginal probability. In practice, we also experimented with updating the prior in the gradient formula but found it made no significant difference in modeling human behavior. Therefore, we adopted the current scheme to reduce the number of free parameters.

The initialization of the representation variable $z$ is critical. In this article, $z$ is a categorical variable that shares the same sample space as the stimulus. The encoder parameters $\theta$ are initialized by passing the product of an identity matrix and an initial value through a softmax function,

$$\psi \left(z | {s;}{\theta }_{0}\right)={{{\rm{softmax}}}}\left({\theta }_{0}{{{\bf{I}}}}\left(s,z\right)\right)$$

(11)

where I is an identity indicator ${{{\bf{I}}}}\left(s,z\right)=1\,{{{\rm{if\,}}}}{z}=s$ ${{{\rm{otherwise}}}}\,0$. We pretrained the encoders to reach 99% discrimination accuracy by tuning the initial value ${\theta }_{0}$. The initial encoder in this case encoded stimuli almost orthogonally, reflecting the “superficially dissimilarity” in the definition of AE. See “Method-Pretrain an encoder” for more details.

In summary, the ECPG model has three parameters: an encoder learning rate ${\alpha }_{\psi }$, a decoder learning rate ${\alpha }_{\rho }$, a simplicity parameter $\lambda$. The stimulus encoder parameters were initialized through pretraining, and the parameters of the decoder were initialized to 0.

The ECPG model’s encoder acts as a generative component, similar to the encoder in the beta variational autoencoder ($\beta$VAE) as described by Higgins et al.¹³ but with a categorical hidden layer instead of a continuous Gaussian distribution. This design facilitates the computation of mutual information and the quantification of representation complexity, building upon the work of Lu et al.⁹⁰.

CPG: the intermediary model

The cascade policy gradient (CPG) model is a special case of the ECPG model, with the simplicity fixed at 0, $\lambda=0$. Therefore, the model has only two parameters: the learning rate for the encoder ${\alpha }_{\psi }$ and the learning rate for the decoder ${\alpha }_{\rho }$.

fRLPG: the feature-based RLPG model

The feature-based models we developed are extensions of the models previously introduced. The primary difference lies in the incorporation of a feature embedding function ${{{\mathcal{F}}}}$ that maps a stimulus $s$ onto a set of features $f$. We crafted a feature embedding function to decompose a greeble stimulus into three distinct features: shape, color, and appendage, using “one-hot encoding” for clear differentiation. For instance, the color “purple” is represented as [1, 0, 0, 0, 0] and “yellow” as [0, 1, 0, 0, 0]. The feature function ${{{\mathcal{F}}}}$ each input stimulus with its one-hot code and concatenates these codes into a 15-dimensional vector $f$, which serves as the model’s input (See Supplementary Fig. S7C).

We modified the policy of the fRLPG model to create a feature-based baseline RL model that does not compress stimuli. This model proposes that visual similarity alone could account for human generalization performance, without the need for a representation compression mechanism. With the feature embedding function ${{{\mathcal{F}}}}$ defined, the policy at trial $t$ can be expressed as follows,

$$\pi \left(a | {{{\mathcal{F}}}}\left({s}_{t}\right);\phi \right)={{{\rm{softmax}}}}\left(\phi \left({f}_{t},a\right)\right)$$

(12)

The parameter $\phi$ now is a 15-by-4 table. As before, the parameter $\phi$ was updated using the policy gradient method Eq. 7, and actions are selected by sampling from the softmax policy, Eq. 12. The model has one parameter, the learning rate of policy ${\alpha }_{\pi }$.

fECPG: the feature-based ECPG model

We modified the ECPG encoder to include the feature embedding function and preserved the previous ECPG decoder formulation (See Supplementary Fig. S7D),

$$\psi \left(z | {{{\mathcal{F}}}}\left({s}_{t}\right);\theta \right)={{{\rm{softmax}}}}\left(\theta \left({f}_{t},z\right)\right)$$

(13)

The parameter $\theta$ now is a 15-by-4 table. The decoder $\rho ({a|z;}\phi )$ remains unchanged.

A new challenge we faced was initializing the encoder parameters for the feature-based model. The previous method, which relied on an identity matrix, was no longer suitable because stimuli with overlapping features naturally appear more similar. For instance, a purple greeble should be more similar to another purple greeble than to a yellow one.

To address this, we introduced a new initialization technique:

First, we measured the visual similarity between a stimulus $s$ and all possible stimuli $z$ (including stimuli $s$ itself) by calculating the dot product of their feature embeddings,

$${{{\rm{sim}}}}\left({{s}},{{z}}\right)=\left\langle {{{\mathcal{F}}}}\left(s\right),{{{\mathcal{F}}}}\left(z\right)\right\rangle \,\forall z\in \left\{x,{x}^{{\prime} },y,{y}^{{\prime} }\right\}$$

(14)

Second, we multiplied these similarity scores by a scalar ${\theta }_{0}$ and passed them through a softmax function to form the representation of stimuli $s$,

$$\bar{\psi }\left(z | s\right)={{{\rm{softmax}}}}\left({\theta }_{0}{{{\rm{sim}}}}\left(s,z\right)\right)$$

(15)

As before, the initial value ${\theta }_{0}$ is tuned through pretraining. This value controls the perceived similarity between stimuli. When ${\theta }_{0}$ is small, stimuli with overlapping features look similar.

Finally, we used the representation $\bar{\psi }\left(z,|,s\right)$ as supervised labels to train the model encoder $\psi \left(z{{{\mathcal{F}}}}\left(s\right),\,\theta \right)$ by minimizing their cross-entropy loss

$${\min }_{\theta }-{\sum}_{z}\bar{\psi }\left(z | s\right)\log \psi \left(z | {{{\mathcal{F}}}}\left(s\right),\theta \right)$$

(16)

Once the training has converged, the encoder for the fECPG model is considered initialized. The subsequent learning and decision-making processes are consistent with the original ECPG model.

The model has three parameters $\{{\alpha }_{\psi },\,{\alpha }_{\rho },\lambda \}$: the learning rate for the encoder ${\alpha }_{\psi }$, the learning rate decoder ${\alpha }_{\rho }$, and the simplicity parameter $\lambda$.

fCPG: the feature-based CPG model

The fCPG model is special case of the fECPG with the simplicity parameter fix to 0, $\lambda=0$. The model has two parameters ${\alpha }_{\psi }$ and ${\alpha }_{\rho }$: the learning rate for the encoder ${\alpha }_{\psi }$, the learning rate for decoder ${\alpha }_{\rho }$.

LC: latent-cause clustering

The LC model is an algorithmic-level model, adopted and modified from Gershman et al.⁵⁴. The central idea of the LC model is to use a non-parametric Bayesian process—Chinese Restaurant Process—to model the cognitive process of latent-cause clustering. The original model cannot be directly applied to the acquired equivalence task, as it is a model of associative learning, not instrumental learning. We modified the model to learn a stimulus-action value function that allows instrumental learning. See more implementation details in Supplementary Note 2.4.

MA: memory-association model

The MA model is an algorithmic-level model that combines memory and association mechanisms. It memorizes stimuli-action pairs and forms associations between stimuli with shared actions or features, using these associations to infer actions for untrained tasks. Stimuli with salient shared features (like “color”) are more easily associated. See more implementation details in Supplementary Note 2.5.

ACL: attention at choice and learning

The ACL model is an algorithmic-level model that model humans’ rewarding feature extraction ability using a linear selective attention mechanism. The model was from Leong et al.⁵⁶ with two modifications. First, the original ACL model was developed on a different paradigm and could not be directly applied to the current generalization task. We modified the ACL model to include a feature-action value $Q(f,a)$ design as in Ballard et al.⁵⁷. Second, instead of using the attention weights calculated from the eye-tracking and functional MRI data, we estimated the attention weight using an attention model. The original authors constructed two types of models to examine the bidirectional relationship between learning and attention. The “choice models” utilize attention data, collected through eye tracking and fMRI, to predict human behaviors. Conversely, the “attention models” use human behavioral data as input and predict the recorded attention data. In this study, we implemented the ACL model by combining the best choice model (the ACL model in the original paper) and the best attention model (the VALUE model in the original paper). We chose this approach because our study lacks attention data, such that we have to use the best attention model to provide reasonable estimation of the attention weights. See more implementation details in Supplementary Note 2.6.

L1PG, L2PG, and DCPG

The three models have similar computational goals with the ECPG model, except that the representation complexity ${I}^{\psi }({S;Z;}\theta )$ terms in Eqs. 8 and 13 was respectively replaced by L1 norm (${\left|\left|\theta \right|\right|}_{1}$), L2 norm (${\left|\left|\theta \right|\right|}_{2}$), and decoder complexity ${I}^{\rho }({Z;A;}\phi )$.

RNDPG: random regularizer policy gradient

The RNDPG considers replacing the mutual information regularizer ${I}^{\psi }\left({S;Z}\right)$ with a random noise penalty ${R}^{\psi }(\varepsilon )$ on the encoder weights,

$${\max }_{\psi,\rho }{E}_{\psi,\rho }\left[r\left({s}_{t},{a}_{t}\right)-b\right]+\lambda {R}^{\psi }\left(\varepsilon \right)$$

(17)

where ${R}^{\psi }\left(\varepsilon \right)$ is a Gaussian noise injected to the encoder weights⁵⁸. Unlike the other regularized policy gradient models, such as ECPG and L1PG, there is no close-form solution for the RNDPG model. Instead, we implemented this model using a sampling method. Please see more implementation details in Supplementary Note 2.7.

Pretrain an encoder

AE describes the phenomenon where generalization between two “superficially dissimilar” stimuli increases after they have been paired with the same actions. To ensure their dissimilarity, we selected stimuli that are easily distinguishable by human participants. We operationally defined this dissimilarity by setting a criterion: all four input stimuli must be classifiable with an accuracy of 99%. In order to accurately model human behaviors in the AE task, all models should undergo pretraining to achieve this level of discrimination accuracy.

The key step of the pretraining is to search for an appropriate ${\theta }_{0}$. This is because all models’ encoders were specially designed such that they can be initialized once the ${\theta }_{0}$ is decided,

$$\bar{\psi }\left(z | {s;}{\theta }_{0}\right)=\left\{\begin{array}{c}{{{\rm{ softmax}}}}\left({\theta }_{0}{{{\bf{I}}}}\left(s,z\right)\right),{{{\rm{for}}}}\; {{{\rm{ECPG}}}}/{{{\rm{CPG}}}}\\ {{{\rm{ softmax}}}}\left({\theta }_{0}{{{\rm{sim}}}}\left(s,z\right)\right),{{{\rm{for}}}}\; {{{\rm{fECPG}}}}/{{{\rm{fCPG}}}}\end{array}\right.$$

(18)

The initial discrimination accuracy of the encoder can be quantified as follows:

$${{{\rm{acc}}}}\left({\theta }_{0}\right)=\frac{1}{4}{\sum}_{i\in \{x,{x}^{{\prime} },y,y^{\prime} \}}\bar{\psi }\left(z=i | s={i;}{\theta }_{0}\right)$$

(19)

Given these constructs, we can search for an appropriate ${\theta }_{0}$ by addressing the following objective,

$${\theta }_{0}^{*}={\arg }{\min }_{{\theta }_{0}}\frac{1}{2}{\left(0.99-{{{\rm{acc}}}}\left({\theta }_{0}\right)\right)}^{2}$$

(20)

Addressing this optimization objective, we initialized ECPG and CPG model using ${\theta }_{0}^{*}=\,5.232$. To initialize the fECPG and fCPG, we used ${\theta }_{0}^{*}=1.459$ for the consistent and conflict case; ${\theta }_{0}^{*}=1.329$ for the control case.

Generate an action

A standard RL problem considers decision-making as sampling an action from the policy $\pi \left(a,|,{s}_{t}\right)$, a categorical distribution over the possible action space. In the AE problem, the possible action space varied from trial to trial. Participants were instructed to choose between ${a}_{1}$ and ${a}_{2}$ in one trial, while they were presented with ${a}_{3}$ and ${a}_{4}$ in another trial. To run both RL-base models in the AE task, we applied a technique called invalid action masking⁹¹.

The simplest masking is to add a large negative number $\zeta$ (in this work, $\zeta=-1e12$) to logits of the actions that are not presented in the current trial. That is, when an RLPG agent needs to choose between ${a}_{1}$ and ${a}_{2}$, we can calculate its renormalized policy as,

$$\widetilde{\pi }\left({a|}{s}_{t};\widetilde{{{\phi }}}\right)={{{\rm{softmax}}}}\left(\widetilde{{{\phi }}}\left(s_t,a\right)\right)$$

(21)

where $\widetilde{\phi }$ is,

$$\widetilde{\phi }\left(s,a\right)=\left\{\begin{array}{c}\phi \left(s,a\right),{{{\rm{if}}}} \, {a} \, {{{\rm{is}}}}\; {{{\rm{valid}}}}\; {{{\rm{action}}}}\; {{{\rm{at}}}} \, t \\ \phi \left(s,a\right)+\zeta,{{{\rm{if}}}} \, {a} \, {{{\rm{is}}}}\; {{{\rm{invalid}}}}\; {{{\rm{action}}}}\; {{{\rm{at}}}} \, t\end{array}\right.$$

(22)

We then sampled from this renormalized policy to model human decision-making.

For the ECPG and CPG models, we masked and re-normalized the decoder for all representations $z$,

$$\widetilde{\rho }\left({a|z;}\widetilde{\phi }\right)={{{\rm{softmax}}}}\left(\widetilde{\phi }\left(z,a\right)\right)$$

(23)

Perturbation-based feature importance

To investigate the importance of different features (color, shape, appendages) to humans, we adopted a perturbation-based measurement approach^52,53, applied to our model fitted to human behavior. This method calculates the importance of each feature by theorizing that if an agent focuses heavily on a particular feature, then a minor perturbation in that feature might lead to significant changes in the output. This perturbation-based importance has been applied to extract measures of attention from large-scale deep reinforcement learning models in artificial intelligence, which was shown to be similar to human eye-tracking attention data⁵³.

In the present work, we calculated the perturbation-based feature importance following the pseudo-algorithm 1 (Supplementary Note 2.2), modified based on the feature importance algorithm described in⁹².

Model fitting

For each model, we estimated its free parameters separately for each subject, using all behavioral data from both the training and testing trials without cross-validation. This approach is consistent with many previous human learning studies, which are often structured with 2 to 4 parallel blocks due to various practical constraints e.g^84,93,94,95. Given the insufficient number of blocks, these studies, including ours, do not meet the prerequisites for effective cross-validation.

The parameters were estimated via maximum a posteriori (MAP):

$${\max }_{\xi }{\sum }_{i=1}^{N}\log \pi \left({a}_{i},|,{s}_{i},{{{\rm{M}}}},\xi \right)+\log p\left(\xi \right)$$

(24)

where ${{{\rm{M}}}}$ refers to the model architecture, and $\xi$ the model parameters. $N$ is the number of trials for each participant. ${s}_{i}$ and ${a}_{i}$ are the presented stimuli and human responses recorded on each trial. We selected a very flat prior $p\left(\xi \right)={{{\rm{Halfnorm}}}}(0,\,50)$ for all parameters with a range of $(0,\infty )$ only to avoid extreme parameter values without biasing estimation. This prior is uninformative yet ensures that parameter estimates remain within a reasonable range. Parameters with a range of $(0,\,1)$ used a uniform prior.

Parameter estimation was performed using the BFGS algorithm, implemented with the Python package scipy.minimize. For each participant, we ran the algorithm with 50 different randomly chosen parameter initializations to avoid local minima in the non-convex landscape.

Simulation

The parameter we are interested in is the simplicity degree ($\lambda$). We simulated the ECPG model’s learning and generalization behaviors by varying $\lambda$, while keeping the other two learning rate parameters constant. In Experiment 1, the learning rate of the encoder was fixed at ${\alpha }_{\psi }=40$, and that of the decoder was fix at ${\alpha }_{\rho }=4$. In Experiment 2, the learning rate of the encoder was fixed at ${\alpha }_{\psi }=8$, and that of the decoder was fix at ${\alpha }_{\rho }=4$.

Correlation between humans’ and models’ probe response

For each participant within a block, we calculated the frequency for each action as an estimation of human probe policy. We applied the same method to the simulated data to obtain models’ probe policy. Subsequently, we computed the Spearman’s correlation between human participants and models based on the probability of selecting actions ${a}_{1}$ and ${a}_{3}$. These two actions sufficiently characterize a policy.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

All data generated in this study, including the raw data and preprocessed data, are publicly available on OSF: https://doi.org/10.17605/OSF.IO/UCTDB.

Code availability

The source code for this study is publicly available on Github: https://doi.org/10.5281/zenodo.15087038.

References

Shepard, R. N. Toward a universal law of generalization for psychological science. Science 237, 1317–1323 (1987).
Article ADS MathSciNet CAS PubMed Google Scholar
Shohamy, D. & Wagner, A. D. Integrating memories in the human brain: hippocampal-midbrain encoding of overlapping events. Neuron 60, 378–389 (2008).
Article CAS PubMed PubMed Central Google Scholar
Sims, C. R. Efficient coding explains the universal law of generalization in human perception. Science 360, 652–656 (2018).
Article ADS CAS PubMed Google Scholar
Li, F-F. et al. A Bayesian approach to unsupervised one-shot learning of object categories. in proceedings ninth IEEE international conference on computer vision. 1134–1141 https://doi.org/10.1109/ICCV.2003.1238476 (2003).
Asadi, A., Abbe, E. & Verdú, S. Chaining mutual information and tightening generalization bounds. In Advances in Neural Information Processing Systems 7245–7254 (NIPS, 2018).
Pensia, A., Jog, V. & Loh, P.-L. Generalization error bounds for noisy, iterative algorithms. in 2018 IEEE International Symposium on Information Theory. 546–550 https://doi.org/10.1109/ISIT.2018.8437571 (2018).
Bengio, Y., Courville, A. & Vincent, P. Representation learning: a review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1798–1828 (2013).
Article PubMed Google Scholar
Goodfellow, I., Bengio, Y. & Courville, A. Deep learning. (MIT Press, 2016).
Radulescu, A., Shin, Y. S. & Niv, Y. Human representation learning. Annu. Rev. Neurosci. 44, 253–273 (2021).
Article CAS PubMed PubMed Central Google Scholar
Niv, Y. Learning task-state representations. Nat. Neurosci. 22, 1544–1553 (2019).
Article CAS PubMed PubMed Central Google Scholar
Flesch, T., Juechems, K., Dumbalska, T., Saxe, A. & Summerfield, C. Orthogonal representations for robust context-dependent task performance in brains and neural networks. Neuron 110, 4212–4219 (2022).
Article CAS PubMed PubMed Central Google Scholar
Nelli, S., Braun, L., Dumbalska, T., Saxe, A. & Summerfield, C. Neural knowledge assembly in humans and neural networks. Neuron 111, 1504–1516 e1509 (2023).
Article CAS PubMed PubMed Central Google Scholar
Higgins, I. et al. Beta-vae: Learning Basic Visual Concepts With A Constrained Variational Framework. in International conference on learning representations (2016).
Li, L., Walsh, T. J. & Littman, M. L. Towards a unified theory of state abstraction for MDPs. in Proceedings of the International Symposium on Artificial Intelligence and Mathematics (2006).
Shwartz-Ziv, R. Information flow in deep neural networks. Ph.D. thesis, Hebrew University, (2022).
Tishby, N., Pereira, F. C. & Bialek, W. The information bottleneck method. In 37th Annual Allerton Conference on Communication, Control, and Computing 368–377 (Springer, 2000).
Sutton, R. S. & Barto, A. G. Reinforcement learning: An introduction. (MIT Press, 2018).
Silver, D., Singh, S., Precup, D. & Sutton, R. S. Reward is enough. Artif. Intell. 299, 103535 (2021).
Article MathSciNet Google Scholar
Rescorla, R. A. A. Theory of pavlovian conditioning: Variations in the effectiveness of reinforcement and non-reinforcement. Classical conditioning. Curr. Res. theory 2, 64–69 (1972).
Google Scholar
Niv, Y. & Langdon, A. Reinforcement learning with Marr. Curr. Opin. Behav. Sci. 11, 67–73 (2016).
Article PubMed PubMed Central Google Scholar
Ribas-Fernandes, J. J. et al. A neural signature of hierarchical reinforcement learning. Neuron 71, 370–379 (2011).
Article CAS PubMed PubMed Central Google Scholar
Xia, L. & Collins, A. G. E. Temporal and state abstractions for efficient learning, transfer, and composition in humans. Psychol. Rev. 128, 643–666 (2021).
Article PubMed PubMed Central Google Scholar
Tomov, M. S., Schulz, E. & Gershman, S. J. Multi-task reinforcement learning in humans. Nat. Hum. Behav. 5, 764–773 (2021).
Article PubMed Google Scholar
Jiang, Y., Mi, Q. & Zhu, L. Neurocomputational mechanism of real-time distributed learning on social networks. Nat. Neurosci. 26, 506–516 (2023).
CAS PubMed Google Scholar
Daw, N. D., Gershman, S. J., Seymour, B., Dayan, P. & Dolan, R. J. Model-based influences on humans’ choices and striatal prediction errors. Neuron 69, 1204–1215 (2011).
Article CAS PubMed PubMed Central Google Scholar
van Opheusden, B. et al. Expertise increases planning depth in human gameplay. Nature 618, 1000–1005 (2023).
Article ADS PubMed Google Scholar
Barto, A. G. et al. Adaptive Critics And The Basal Ganglia. in Models of information processing in the basal ganglia. 215–232 (1995).
Montague, P. R., Dayan, P. & Sejnowski, T. J. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 16, 1936–1947 (1996).
Article CAS PubMed PubMed Central Google Scholar
Niv, Y. Reinforcement learning in the brain. J. Math. Psychol. 53, 139–154 (2009).
Article MathSciNet Google Scholar
Schultz, W., Dayan, P. & Montague, P. R. A neural substrate of prediction and reward. Science 275, 1593–1599 (1997).
Article CAS PubMed Google Scholar
Gershman, S. J. & Daw, N. D. Reinforcement learning and episodic memory in humans and animals: an integrative framework. Annu. Rev. Psychol. 68, 101–128 (2017).
Article PubMed Google Scholar
Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).
Article ADS CAS PubMed Google Scholar
Ho, M. K. et al. People construct simplified mental representations to plan. Nature 606, 129–136 (2022).
Article ADS CAS PubMed Google Scholar
Barlow, H. B. Possible principles underlying the transformation of sensory messages. Sens. Commun. 1, 217–233 (1961).
Google Scholar
Miller, G. A. The magical number seven plus or minus two: some limits on our capacity for processing information. Psychol. Rev. 63, 81–97 (1956).
Article CAS PubMed Google Scholar
Wei, X. X. & Stocker, A. A. A Bayesian observer model constrained by efficient coding can explain ‘anti-Bayesian’ percepts. Nat. Neurosci. 18, 1509–1517 (2015).
Article CAS PubMed Google Scholar
Simoncelli, E. P. & Olshausen, B. A. Natural image statistics and neural representation. Annu. Rev. Neurosci. 24, 1193–1216 (2001).
Article CAS PubMed Google Scholar
Sims, C. R. Rate-distortion theory and human perception. Cognition 152, 181–198 (2016).
Article PubMed Google Scholar
Sims, C. R., Jacobs, R. A. & Knill, D. C. An ideal observer analysis of visual working memory. Psychol. Rev. 119, 807–830 (2012).
Article PubMed PubMed Central Google Scholar
Bates, C. J., Lerch, R. A., Sims, C. R. & Jacobs, R. A. Adaptive allocation of human visual working memory capacity during statistical and categorical learning. J. Vis. 19, 11 (2019).
Article PubMed Google Scholar
Lerch, R. & Sims, C. R. Modeling associative motor learning through capacity-limited reinforcement learning. J. Vis. 21, 2782–2782 (2021).
Google Scholar
Botvinick, M., Weinstein, A., Solway, A. & Barto, A. Reinforcement learning, efficient coding, and the statistics of natural tasks. Curr. Opin. Behav. Sci. 5, 71–77 (2015).
Article Google Scholar
Myers, C. E. et al. Dissociating medial temporal and basal ganglia memory systems with a latent learning task. Neuropsychologia 41, 1919–1928 (2003).
Article PubMed Google Scholar
Meeter, M., Shohamy, D. & Myers, C. E. Acquired equivalence changes stimulus representations. J. Exp. Anal. Behav. 91, 127–141 (2009).
Article CAS PubMed PubMed Central Google Scholar
Collins, A. G. E. & Frank, M. J. Neural signature of hierarchically structured expectations predicts clustering and transfer of rule sets in reinforcement learning. Cognition 152, 160–169 (2016).
Article PubMed PubMed Central Google Scholar
Collins, A. G. & Frank, M. J. Cognitive control over learning: creating, clustering, and generalizing task-set structure. Psychol. Rev. 120, 190–229 (2013).
Article PubMed PubMed Central Google Scholar
Marr, D. Vision: A computational investigation into the human representation and processing of visual information. (MIT Press, 1982).
Niv, Y. et al. Reinforcement learning in multidimensional environments relies on attention mechanisms. J. Neurosci. 35, 8145–8157 (2015).
Article CAS PubMed PubMed Central Google Scholar
Williams, R. J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 8, 229–256 (1992).
Article Google Scholar
Rousseeuw, P. J. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 20, 53–65 (1987).
Article Google Scholar
Rigoux, L., Stephan, K. E., Friston, K. J. & Daunizeau, J. Bayesian model selection for group studies—revisited. Neuroimage 84, 971–985 (2014).
Article CAS PubMed Google Scholar
Greydanus, S., Koul, A., Dodge, J. & Fern, A. Visualizing and understanding atari agents. in International conference on machine learning. 1792–1801 (2018).
Guo, S. S. et al. Machine versus human attention in deep reinforcement learning tasks. in Adv. Neural Information Processing Systems. 25370–25385 (2021).
Gershman, S. J., Monfils, M. H., Norman, K. A. & Niv, Y. The computational nature of memory modification. Elife 6, e23763 (2017). https://doi.org/10.7554/eLife.23763
Gershman, S. J., Blei, D. M. & Niv, Y. Context, learning, and extinction. Psychol. Rev. 117, 197–209 (2010).
Article PubMed Google Scholar
Leong, Y. C., Radulescu, A., Daniel, R., DeWoskin, V. & Niv, Y. Dynamic Interaction between Reinforcement Learning and Attention in Multidimensional Environments. Neuron 93, 451–463 (2017).
Article CAS PubMed PubMed Central Google Scholar
Ballard, I., Miller, E. M., Piantadosi, S. T., Goodman, N. D. & McClure, S. M. Beyond reward prediction errors: human striatum updates rule values during learning. Cereb. Cortex 28, 3965–3975 (2018).
Article PubMed Google Scholar
Noh, H., You, T., Mun, J. & Han, B. Regularizing deep neural networks by noise: Its interpretation and optimization. in Advances in neural information processing systems. 5115–5124 (2017).
Hall, G. Perceptual and Associative Learning. (Oxford University Press, 1991).
Urcuioli, P. J. & Vasconcelos, M. Effects of within-class differences in sample responding on acquired sample equivalence. J. Exp. Anal. Behav. 89, 341–358 (2008).
Article PubMed PubMed Central Google Scholar
Bonardi, C., Graham, S., Hall, G. & Mitchell, C. Acquired distinctiveness and equivalence in human discrimination learning: evidence for an attentional process. Psychon. Bull. Rev. 12, 88–92 (2005).
Article PubMed Google Scholar
Farkas, M. et al. Associative learning in deficit and nondeficit schizophrenia. Neuroreport 19, 55–58 (2008).
Article PubMed Google Scholar
Keri, S., Nagy, O., Kelemen, O., Myers, C. E. & Gluck, M. A. Dissociation between medial temporal lobe and basal ganglia memory systems in schizophrenia. Schizophr. Res. 77, 321–328 (2005).
Article PubMed Google Scholar
Bodi, N., Csibri, E., Myers, C. E., Gluck, M. A. & Keri, S. Associative learning, acquired equivalence, and flexible generalization of knowledge in mild Alzheimer disease. Cogn. Behav. Neurol. 22, 89–94 (2009).
Article PubMed Google Scholar
Berger, S. & Machens, C. K. Compact task representations as a normative model for higher-order brain activity. in Advances in Neural Information Processing Systems. 3209–3219 (2020).
Franklin, N. T. & Frank, M. J. Generalizing to generalize: humans flexibly switch between compositional and conjunctive structures during reinforcement learning. PLoS Comput. Biol. 16, e1007720 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Frydman, C. & Jin, L. J. Efficient coding and risky choice. Q. J. Econ. 137, 161–213 (2022).
Article Google Scholar
Jaskir, A. & Frank, M. J. On the normative advantages of dopamine and striatal opponency for learning and choice. Elife 12 (2023). https://doi.org/10.7554/eLife.85107
Luettgau, L. et al. Decomposing dynamical subprocesses for compositional generalization. Proc. Natl Acad. Sci. 121, e2408134121 (2024).
Article CAS PubMed PubMed Central Google Scholar
Gershman, S. J. & Cikara, M. Structure learning principles of stereotype change. Psychon. Bull. Rev. 30, 1273–1293 (2023).
Article PubMed Google Scholar
Lehnert, L., Littman, M. L. & Frank, M. J. Reward-predictive representations generalize across tasks in reinforcement learning. PLoS Comput. Biol. 16, e1008317 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Mack, M. L., Love, B. C. & Preston, A. R. Dynamic updating of hippocampal object representations reflects new conceptual knowledge. Proc. Natl Acad. Sci. 113, 13203–13208 (2016).
Article ADS CAS PubMed PubMed Central Google Scholar
Markovic, D., Glascher, J., Bossaerts, P., O’Doherty, J. & Kiebel, S. J. Modeling the evolution of beliefs using an attentional focus mechanism. PLoS Comput. Biol. 11, e1004558 (2015).
Article ADS PubMed PubMed Central Google Scholar
Konidaris, G. On the necessity of abstraction. Curr. Opin. Behav. Sci. 29, 1–7 (2019).
Article PubMed Google Scholar
Chelombiev, I., Houghton, C. & O’Donnell, C. Adaptive estimators show information compression in deep neural networks. In Proc. International Conference on Learning Representations (ICLR, 2019).
Islam, R. et al. Representation learning in deep RL via discrete information bottleneck. In Proc. 26th International Conference on Artificial Intelligence and Statistics 8699–8722 (AISTATS, 2023).
Rakelly, K., Gupta, A., Florensa, C. & Levine, S. Which Mutual-Information Representation Learning Objectives are Sufficient for Control? in Advances in Neural Information Processing Systems. 26345-26357 (2021).
Ferns, N. & Precup, D. Bisimulation metrics are optimal value functions. in Proceedings of the Thirtieth Conference on Uncertainty in Artificial Intelligence. 210–219 (2014).
Gershman, S. J., Horvitz, E. J. & Tenenbaum, J. B. Computational rationality: a converging paradigm for intelligence in brains, minds, and machines. Science 349, 273–278 (2015).
Article ADS MathSciNet CAS PubMed Google Scholar
Griffiths, T. L., Lieder, F. & Goodman, N. D. Rational use of cognitive resources: levels of analysis between the computational and the algorithmic. Top. Cogn. Sci. 7, 217–229 (2015).
Article PubMed Google Scholar
Von Neumann, J. & Morgenstern, O. Theory of games and economic behavior, 2nd rev. (1947).
Zenon, A., Solopchuk, O. & Pezzulo, G. An information-theoretic perspective on the costs of cognition. Neuropsychologia 123, 5–18 (2019).
Article PubMed Google Scholar
Lieder, F. & Griffiths, T. L. Resource-rational analysis: understanding human cognition as the optimal use of limited computational resources. Behav. Brain Sci. 43, e1 (2020).
Article Google Scholar
Gershman, S. J. Origin of perseveration in the trade-off between reward and complexity. Cognition 204, 104394 (2020).
Article PubMed Google Scholar
Gauthier, I. & Tarr, M. J. Becoming a “Greeble” expert: exploring mechanisms for face recognition. Vis. Res. 37, 1673–1682 (1997).
Article CAS PubMed Google Scholar
Gauthier, I., Tarr, M. J., Anderson, A. W., Skudlarski, P. & Gore, J. C. Activation of the middle fusiform ‘face area’ increases with expertise in recognizing novel objects. Nat. Neurosci. 2, 568–573 (1999).
Article CAS PubMed Google Scholar
Zhou, B., Lapedriza, A., Xiao, J., Torralba, A. & Oliva, A. Learning deep features for scene recognition using places database. in Proceedings of the 28th International Conference on Neural Information Processing Systems - 1, 487–495 (2014).
Crowston, K. Amazon mechanical turk: A research tool for organizations and information systems scholars. in Shaping the Future of ICT Research. Methods and Approaches: IFIP WG 8.2, Working Conference, Tampa, FL, USA, 210–221 (2012).
Paszke, A. et al. Pytorch: An imperative style, high-performance deep learning library. in Advances in neural information processing systems. 8026–8037 (2019).
Lu, X., Lee, K., Abbeel, P. & Tiomkin, S. Dynamics generalization via information bottleneck in deep reinforcement learning. In CoRR (2020).
Huang, S. & Ontañón, S. A closer look at invalid action masking in policy gradient algorithms. In Proc. Thirty-Fifth International Florida Artificial Intelligence Research Society Conference (2022).
Fisher, A., Rudin, C. & Dominici, F. All models are wrong, but many are useful: learning a variable’s importance by studying an entire class of prediction models simultaneously. J. Mach. Learn. Res. 20, 1–81 (2019).
MathSciNet CAS Google Scholar
Daw, N. D. Trial-by-trial data analysis using computational models. Decis. Mak., affect, Learn.: Atten. Perform. XXIII 23, 3–38 (2011).
Article Google Scholar
Browning, M., Behrens, T. E., Jocham, G., O’Reilly, J. X. & Bishop, S. J. Anxious individuals have difficulty learning the causal statistics of aversive environments. Nat. Neurosci. 18, 590–596 (2015).
Article CAS PubMed PubMed Central Google Scholar
Rac-Lubashevsky, R., Cremer, A., Collins, A. G. E., Frank, M. J. & Schwabe, L. Neural index of reinforcement learning predicts improved stimulus-response retention under high working memory load. J. Neurosci. 43, 3131–3143 (2023).
Article CAS PubMed PubMed Central Google Scholar

Download references

Acknowledgements

We thank Isabel Gauthier and Michael Tarr for granting permission to use their “greebles” stimuli, originally sourced from http://www.tarrlab.org/. We also thank Bolei Zhou et al. for making their data set publicly available at http://places.csail.mit.edu/downloadData.html. This research is supported by the National Natural Science Foundation of China (32441102 [Z.F.]), Shanghai Municipal Education Commission (2024AIZD014 [Z.F.]), Key Laboratory of Brain-Machine Intelligence for Information Behavior- Ministry of Education (2023JYBKFKT005 [Z.F.]), and the China Postdoctoral Science Foundation (2024M761999 [Z.F.]).

Author information

Authors and Affiliations

Brain Health Institute, National Center for Mental Disorders, Shanghai Mental Health Center, Shanghai Jiao Tong University School of Medicine and School of Psychology, Shanghai, 200030, China
Zeming Fang
Key Laboratory of Brain-Machine Intelligence for Information Behavior-Ministry of Education, Shanghai International Studies University, Shanghai, China
Zeming Fang
Department of Cognitive Science, Rensselaer Polytechnic Institute, Troy, NY, USA
Chris R. Sims

Authors

Zeming Fang
Chris R. Sims

Contributions

Z.F. performed experiments. C.R.S supervised the work. Both authors designed research, analyzed data, discussed the results and wrote the paper.

Corresponding author

Correspondence to Zeming Fang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Fang, Z., Sims, C.R. Humans learn generalizable representations through efficient coding. Nat Commun 16, 3989 (2025). https://doi.org/10.1038/s41467-025-58848-6

Download citation

Received: 14 December 2023
Accepted: 01 April 2025
Published: 29 April 2025
Version of record: 29 April 2025
DOI: https://doi.org/10.1038/s41467-025-58848-6