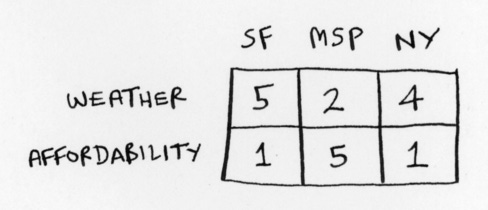
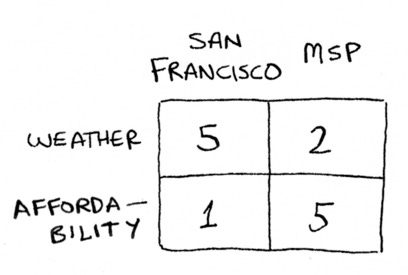
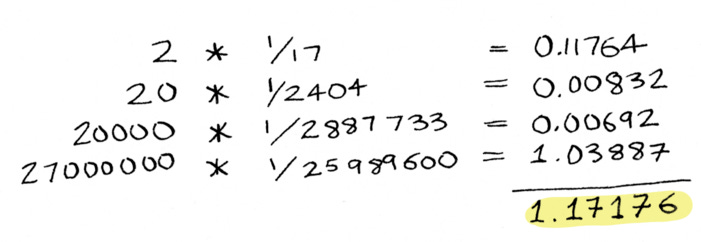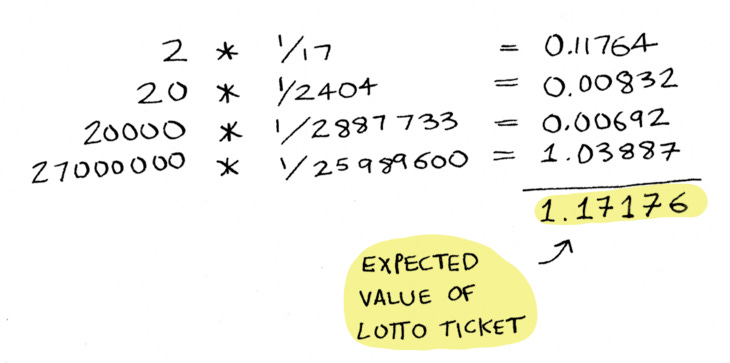When my wife and I were deciding which city to live in, we made a list of cities, and scored each city based on some criteria. Here’s San Francisco and Minneapolis, for example, on weather and affordability.
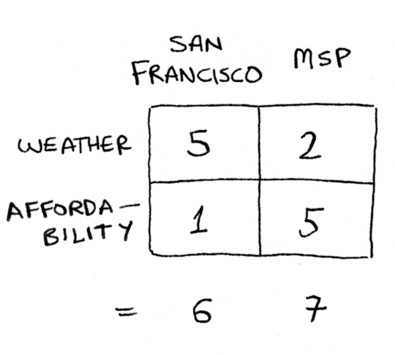
You can see we loved the weather in San Francisco, but Minneapolis was way cheaper to live in. After this was done, we just added up the columns to figure out which city to live in!
Here’s the thing, though: I really liked the weather in San Francisco. I wanted some way to do this calculation, but have the weather matter more. Well, I could do that by using weights.
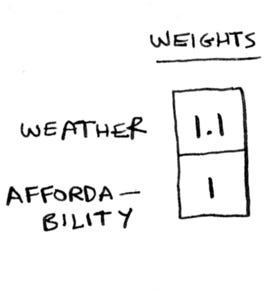
If I wanted the weather to matter 10% more, I could multiply by 1.1 before doing the addition.
(I also multiplied the affordability by 1 to show that I’m keeping it the same).
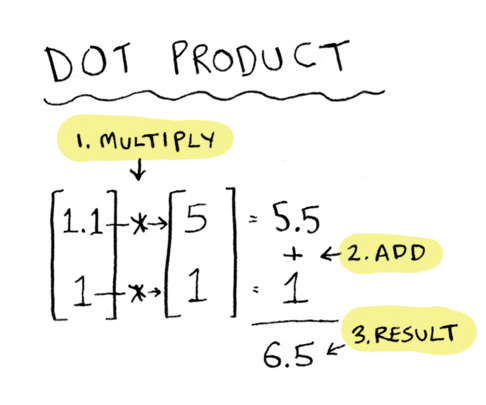
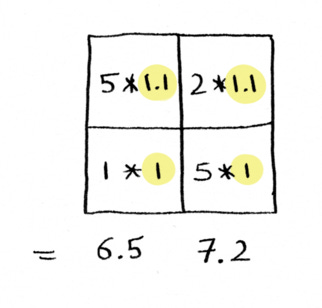
This is the essence of what a dot product is! Earlier I was adding up the numbers. Now I’m weighting the numbers before I add them
A dot product is a type of weighted sum.
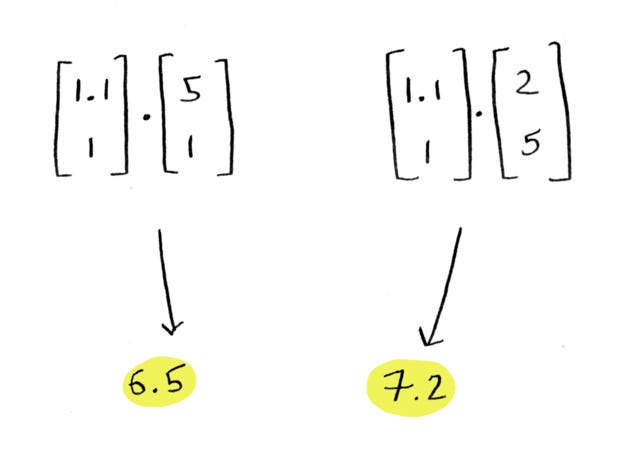
Remember vectors from last chapter? Well, the dot product is an operation you perform on two vectors. Let’s write the above as a vector. For example, here are the scores for San Francisco as a vector
Here are the weights as a vector
We simply multiply the numbers by the weights and then add:
Tada! We just took a dot product of two vectors! It’s a straightforward operation.
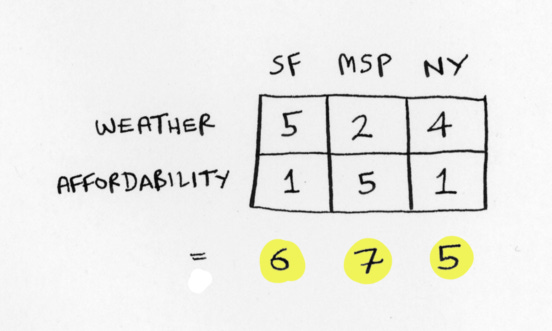
Let’s see the same example with three cities. Here are our three cities with scores for weather and affordability:
The simple way to calculate scores would be to just add up the numbers:
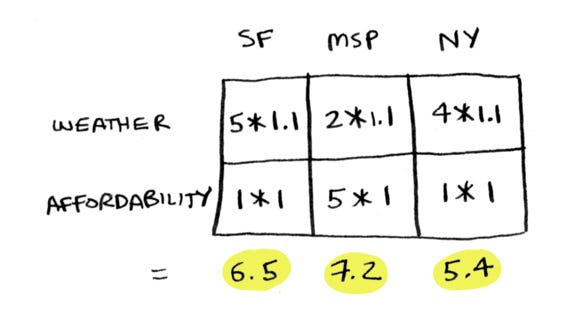
But instead, we’re going to take the dot product:
We are taking three separate dot products here. For each city, we multiply its scores by the weights:
I’m saying that now to make it clear that we’re not taking the dot product of three vectors. That’s impossible, we can only take the dot product of two vectors. Instead we are taking three separate dot products. More on this later.
Now let’s look at another example. Let’s look at the Minnesota lottery.
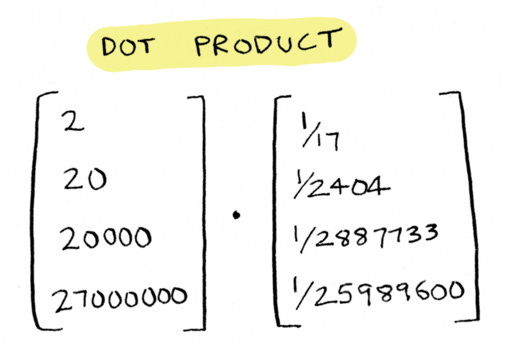
It takes $2 to buy a ticket for the Minnesota lottery. Here are the odds:
So your odds of winning $2 are 1 in 17, your odds of winning $20 are 1 in 2404, etc. Given this information, how do you calculate how much a single ticket is worth, on average?
To find out, we again need to take the dot product. Here are the two vectors:
Prize money on the left, probability of winning on the right. Let’s see the calculation:
The ticket is worth $1.17176. It costs $2, so on average you can expect to lose money, which is what we knew already.
Same as the cities example, we are weighting the numbers, except this time the weights are the probability that we win that much money. The final number is called the expected value.
It’s the expected value of our ticket.
That’s all for dot products. It’s a straightforward operation, but one that’s important to know for matrix multiplication, which is the topic of the next chapter.
A dot product is a type of weighted sum, and is an operation you do on two vectors. You multiply each element of the vectors together, then add up the results:
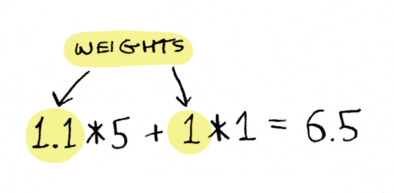
![[5 1] [5 1]](https://substackcdn.com/image/fetch/$s_!cVCy!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F25a22cfe-3e41-4dc8-a01e-fa6f46f3f0af_158x254.png)
![[1.1 1] [1.1 1]](https://substackcdn.com/image/fetch/$s_!IdFP!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2Fe7b8cb6a-a37b-4010-be19-9a6504910ea1_158x256.png)