We instinctively know that “bank” means something completely different in “river bank” versus “money bank”, but how do you teach that distinction to a computer? We keep hearing that “Attention is All You Need”, but why? The answer lies in a deceptively simple mechanism that eventually allowed models to stop looking at words in isolation and start understanding the relationships between them.
Context
This post is inspired by a YouTube series that finally made the attention mechanism click for me. If you understand Hindi, I highly recommend watching the original video below—it’s distinctively clear. What follows is my attempt to solidify my own understanding (and hopefully yours) by rewriting that intuition.
This post assumes you already have some basic understanding of NLP and ML; otherwise, the explanations would get way too long for our goldfish-level attention spans (mine included, I’m kinda lazy, to write too much lol).
Embeddings: The Zeros and Ones of NLP
Before we even get to Attention, we need to talk about embeddings, because they’re the foundation of pretty much everything in modern NLP. If you strip away the hype, embeddings are just a way of turning words into numbers because, well, your computer doesn’t understand English, Mandarin, or emoji. It just understands numbers and we need to represent our words into numbers.
But, how do we convert words into meaningful numbers?
From Counting Words… to Understanding Words
In the early days, our approach was quite simple: count stuff.
How many times does the word appear? Which words appear near each other? Can we build a giant sparse vector with counts?
These methods (Bag-of-Words, TF-IDF) were okay for basic tasks, but they treated each word like a unique card, no relationships, no meaning, no nuance.
Then came the first major leap: learn the embeddings instead of designing them.
This gave us Word2Vec, GloVe, and friends, models that learned to place words in a vector space where similar words end up close together. At this point, embeddings stopped being plain numbers and started becoming… well, meaningful.
That’s how we got the now iconic example:
vector(“queen”) – vector(“woman”) + vector(“man”) ≈ vector(“king”)
When you see that for the first time, it genuinely feels like cheating. Suddenly, algebra is capturing actual semantic relationships. (Yes, the same linear algebra you swore you’d never need. Welcome back. It’s here to stay.)
But there is still one issue.
One word = one vector = one meaning.
But language doesn’t behave like that. Again consider the example:
“He sat on the river bank.”
“He deposited cash at the bank.”
Very same set of words, yet completely different meaning.
Old-school embeddings couldn’t handle this. The word “Bank” had a single vector, no matter where it appeared.
Intuition Behind Self Attention (Context-Aware Embeddings)
To truly understand language, word representations must change depending on the sentence they appear in.
The word “bank” means very different things in “He sat on the river bank.” versus “He deposited cash at the bank.” Even though the word is the same, its meaning is determined by the surrounding context. This means we need a way to convert “bank” into different vectors depending on the words around it.
This is where self-attention comes into play. Self-attention allows a model to dynamically adjust a word’s embedding by looking at other words in the sentence and weighing their relevance. In effect, the representation of “bank” is reshaped by its context.
The following animation is a simplified view of this process: starting from the base embedding of “bank,” the model shifts that vector as contextual words are introduced, producing a context-aware representation.
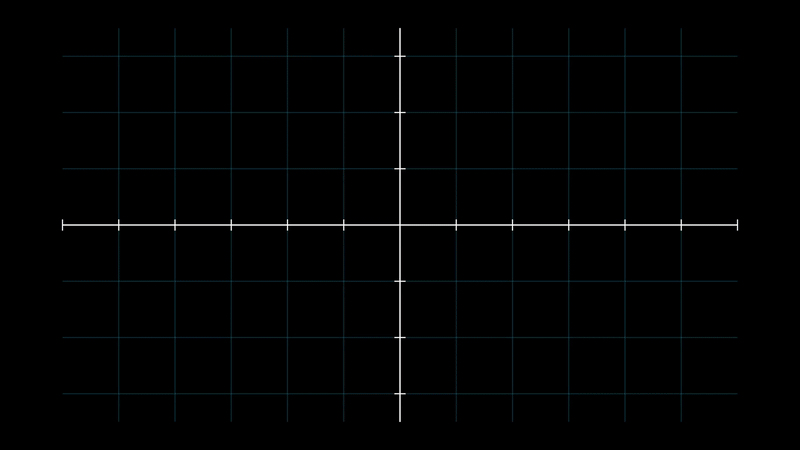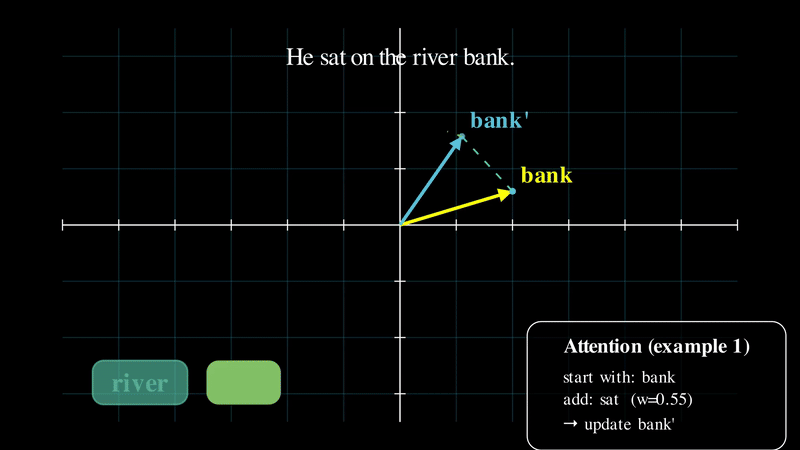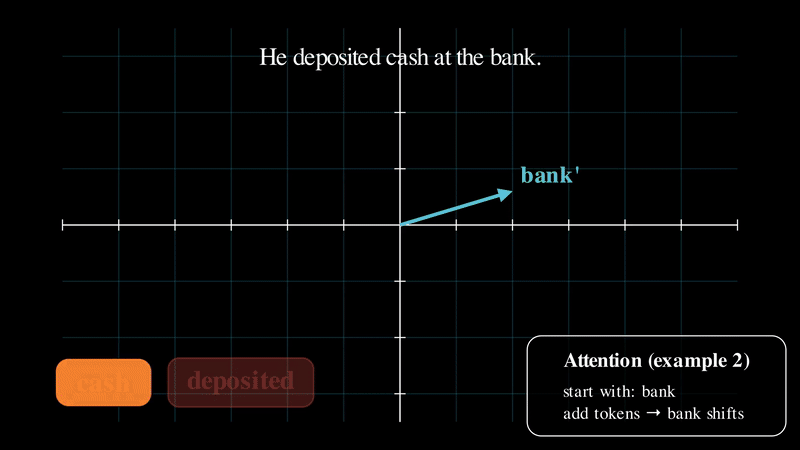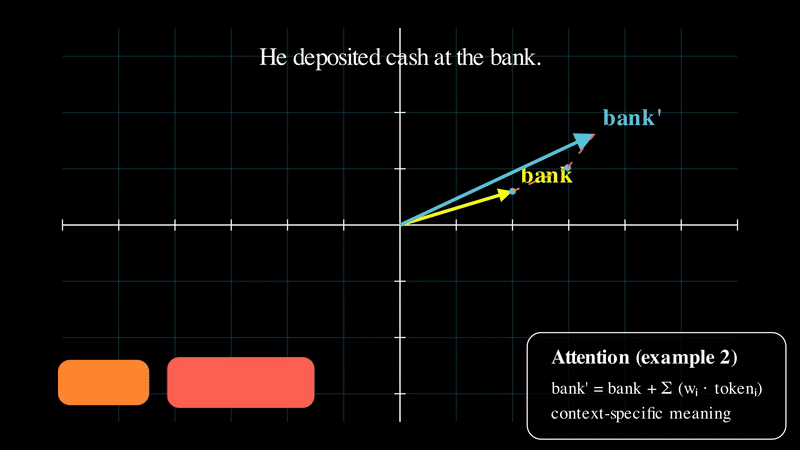
As you can see in the simplified illustration above, the embedding vector for “bank” changes as different surrounding words are introduced. This is the core idea behind attention. Now that we have an intuitive understanding of what attention does, let’s dive into how it that vector transformation actually works.
Mathematics behind Self Attention
Ok, so what is the easiest way to update the embedding of a word based on surrounding word? Maybe start with a table where each word gets their own unique vector. Or lets say each word is mapped to a vector. Then in order to calculate the vector of a word based on surrounding words, the first intuition would be to simply add the embeddings of surrounding words.
“He sat on the river bank.”
\[ \mathbf{v}_{\text{bank}}^{\text{context}} = \mathbf{v}_{\text{bank}} + \mathbf{v}_{\text{he}} + \mathbf{v}_{\text{sat}} + \mathbf{v}_{\text{on}} + \mathbf{v}_{\text{the}} + \mathbf{v}_{\text{river}} \]
But this approach has a problem: it treats every surrounding word as equally important when updating the vector for “bank.” In reality, some words contribute much more to meaning than others.
For example, in “He sat on the river bank,” the word “river” matters far more than “he” when deciding what “bank” means.
So instead of a plain sum, what if we compute a weighted sum giving more influence to important context words and less to irrelevant ones? Here, each weight 𝑤 represents how much attention we pay to a particular word when interpreting “bank".
\[ \mathbf{v}_{\text{bank}}^{\text{context}} = \mathbf{v}_{\text{bank}} + w_{\text{he}} \mathbf{v}_{\text{he}} + w_{\text{sat}} \mathbf{v}_{\text{sat}} + w_{\text{on}} \mathbf{v}_{\text{on}} + w_{\text{the}} \mathbf{v}_{\text{the}} + w_{\text{river}} \mathbf{v}_{\text{river}} \]
The self-attention mechanism is all about finding the values of these weights. So, how exactly do we do that?
Step 1: Prepare the Input
First, we take the embedding vector and add some positional information to it. (Don’t worry about the positional encoding for now; explaining that would require its own dedicated blog post).
Step 2: Create Query, Key, and Value Vectors
Once we have this input, we create three copies of the same embedding vector. We call these copies Query (\(q\)), Key (\(k\)), and Value (\(v\)).
\[ q_{\text{bank}} = \mathbf{v}_{\text{bank}}, \quad k_{\text{bank}} = \mathbf{v}_{\text{bank}}, \quad v_{\text{bank}} = \mathbf{v}_{\text{bank}} \]
And similarly for every other word in the sentence:
\[ q_{\text{river}} = \mathbf{v}_{\text{river}}, \quad k_{\text{river}} = \mathbf{v}_{\text{river}}, \quad v_{\text{river}} = \mathbf{v}_{\text{river}} \]
Note: There is a slight twist to this later (involving learned weight matrices), but for the sake of intuition, let’s assume for now that these three are exact replicas of the input embedding.
Step 3: Compute Attention Scores
Now comes the key insight. To find the weight (attention score) between two words, we take the dot product of the Query vector of the current word with the Key vector of the context word.
Why dot product? Because if two vectors point in similar directions (i.e., the words are semantically related), the dot product will be large. If they’re unrelated, it will be small.
For “bank” attending to every word in the sentence:
\[ \text{score}(\text{bank}, \text{he}) = q_{\text{bank}} \cdot k_{\text{he}} \] \[ \text{score}(\text{bank}, \text{sat}) = q_{\text{bank}} \cdot k_{\text{sat}} \] \[ \vdots \] \[ \text{score}(\text{bank}, \text{river}) = q_{\text{bank}} \cdot k_{\text{river}} \]
Or more compactly, for any context word \(i\):
\[ \text{score}(\text{bank}, i) = q_{\text{bank}} \cdot k_i \]
Step 4: Normalize with Softmax
These raw scores can be any number. To turn them into proper weights that sum to 1, we pass all the scores through a Softmax function:
\[ w_{\text{he}} = \frac{e^{\text{score}(\text{bank}, \text{he})}}{\sum_j e^{\text{score}(\text{bank}, j)}}, \quad w_{\text{sat}} = \frac{e^{\text{score}(\text{bank}, \text{sat})}}{\sum_j e^{\text{score}(\text{bank}, j)}}, \quad \ldots \]
Or simply:
\[ w_i = \text{softmax}\left( q_{\text{bank}} \cdot k_i \right) \]
Now all the weights \(w_i\) are positive and sum to 1, exactly what we need for a weighted average.
Step 5: Compute the Weighted Sum
Finally, we multiply each normalized weight by its corresponding Value (\(v\)) vector and sum them all up:
\[ \mathbf{v}_{\text{bank}}^{\text{context}} = w_{\text{he}} \cdot v_{\text{he}} + w_{\text{sat}} \cdot v_{\text{sat}} + w_{\text{on}} \cdot v_{\text{on}} + w_{\text{the}} \cdot v_{\text{the}} + w_{\text{river}} \cdot v_{\text{river}} + w_{\text{bank}} \cdot v_{\text{bank}} \]
Or in compact notation:
\[ \mathbf{v}_{\text{bank}}^{\text{context}} = \sum_{i} w_i \cdot v_i = \sum_{i} \text{softmax}\left( q_{\text{bank}} \cdot k_i \right) \cdot v_i \]
And there you have it, the context-aware embedding we were looking for! The word “river” will naturally get a higher weight when determining what “bank” means, simply because their embeddings are more aligned in the vector space.
The Twist: Learnable Weight Matrices
Remember how I said Query, Key, and Value are just copies of the embedding vector? That was a simplification. In reality, there’s a crucial twist.
If \(q\), \(k\), and \(v\) were just copies, we’d be stuck with whatever relationships the original embeddings capture. But what if the model could learn what to look for? What if it could discover patterns in the training data that tell it: “when you see ‘river’, pay extra attention to nearby nouns”?
This is where learnable weight matrices come in. Instead of copying the embedding directly, we multiply it by three distinct weight matrices: \(W_Q\), \(W_K\), and \(W_V\).
\[ q_{\text{bank}} = W_Q \cdot \mathbf{v}_{\text{bank}}, \quad k_{\text{bank}} = W_K \cdot \mathbf{v}_{\text{bank}}, \quad v_{\text{bank}} = W_V \cdot \mathbf{v}_{\text{bank}} \]
These matrices are learned during training on massive text corpora. Through backpropagation, the model figures out:
- \(W_Q\): What should I be looking for? (the “question” I’m asking)
- \(W_K\): What information do I contain that others might need? (my “label”)
- \(W_V\): What information should I contribute to the final output?
This is the magic that lets transformers understand language so well, they learn these relationships from billions of words of text, capturing nuances that we could never hand-code.
Putting It All Together
Here’s a visual summary of everything we’ve covered:
That’s it. Dot products to measure similarity, softmax to normalize, weighted sums to blend and learnable matrices to make it all trainable. This single mechanism, stacked and repeated, powers GPT, BERT, and every LLM you’ve heard of.
Pretty wild what a weighted sum can do!