Can you tile a 25x25 square with a mixture of 2x2 squares and 3x3 squares?

asked Apr 18, 2024 at 5:31

I think the answer is

Impossible.

Consider the following image:

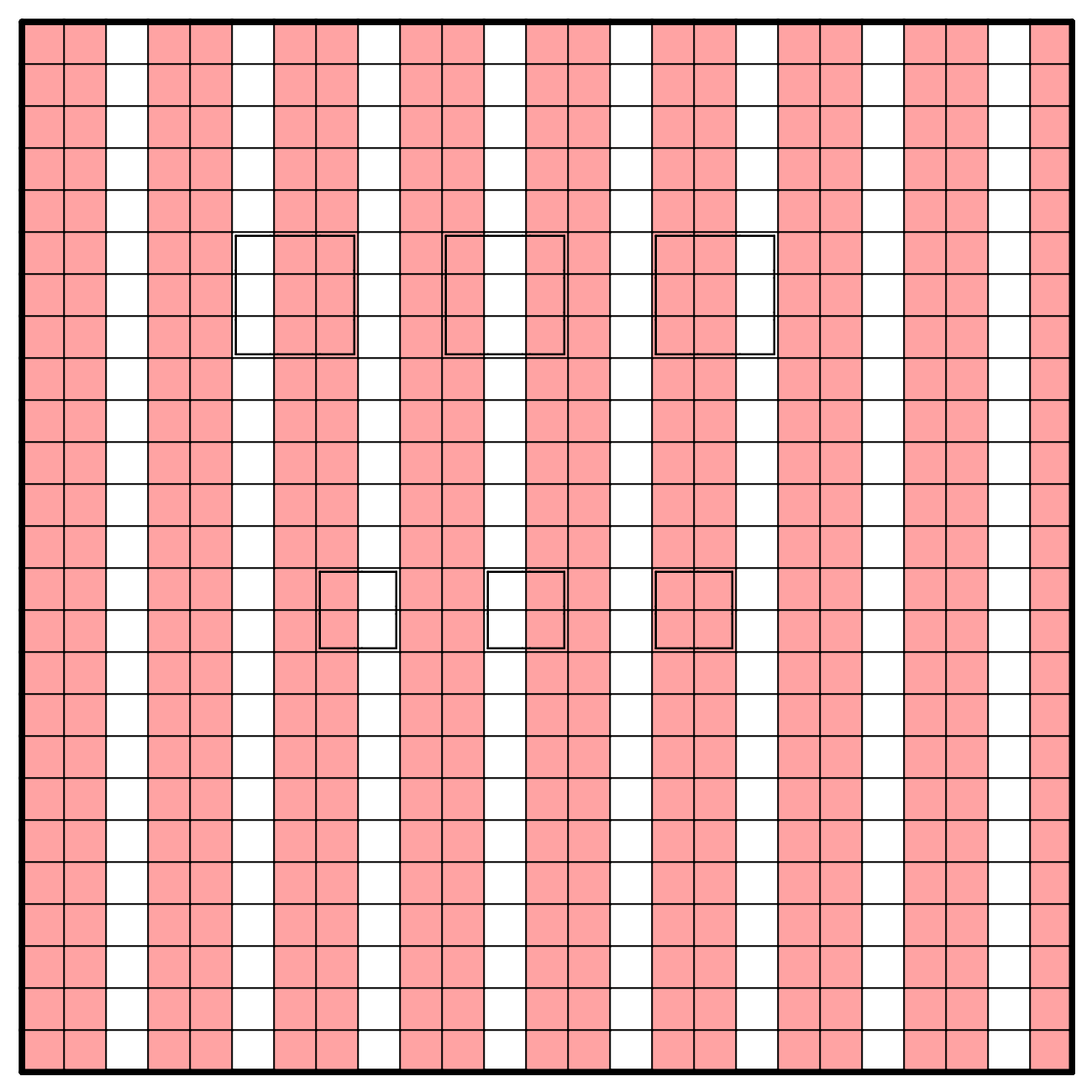
In this striped coloring, $17 \times 25$ cells are colored in total, which is odd. On the other hand, every placement of a $3 \times 3$ square covers exactly $6$ colored cells, and that of a $2 \times 2$ square covers either $2$ or $4$ colored cells. This means any nonoverlapping placement of $2 \times 2$ and $3 \times 3$ squares can only cover an even number of colored cells, and therefore cannot cover all colored cells on the grid.

Generalizing this result, the question "For which $n$ can an $n \times n$ square be tiled with $2 \times 2$ and $3 \times 3$ squares?" can be fully answered:

• If $n$ is even, it can be fully tiled with $2 \times 2$ squares.
• If $n$ is a multiple of $3$, it can be fully tiled with $3 \times 3$ squares.
• If $n$ is $1 \bmod 6$, the even-odd argument on the same coloring pattern applies, and therefore a tiling does not exist.
• If $n$ is $5 \bmod 6$, the same argument can be made using the same pattern but shifted right by one column (so that the leftmost column is not colored). This creates a coloring with the exact same property. Therefore a tiling does not exist in this case either.

Very similar to @Bubbler's solution but perhaps a bit simpler:

Label each square in row r with (-1)^r. Then the sum over all labels is 25 (if you count rows from 0). The sum over all labels covered by a tile 0,-3 or 3. In any case it is divisible by 3. Therefore a tiling cannot exist.

A classic problem of:

invariants!

Consider the coloring where the 3rd, 6th, 9th... until 24th column are shaded. Then 2x2 and 3x3 squares both cover an even number of unshaded squares. This is an invariant! Since there are an odd number of unshaded squares in a 25x25 grid, we are done.

Since the tiles to use are squares they can only fill in a rectangular space. 25x25 is square so the obvious problem isn't an issue.

I can only think of 3 ways that these tiles can fill in a square area:

1. using only 2x2 tiles

2. using only 3x3 tiles

3. or combining them into effective 6x6 tiles like so:

Next we need to look at the factors of the length of the square space. For example a 24 square space has factors including 2, 3, and 6 which means

that all 3 methods can fill in that space.

However the question's area to fill is 25x25 which only has a factor of 5 which means

that 2, 3, and 6 can never fill in the space.

Therefore the answer is:

impossible.

Yes this is possible.

The board is 25x25... A ring of 2x2 tiles round the exterior would leave an internal space of 21x21. This internal space would allow exactly 7x7 of the 3x3 tiles (3x7)x(3x7).