Research Log // January 2026
A computational numerical experiement.
I recently became interested in the unary number representation system, and after developing my understanding of this topic I decided to implement a unary system in python where the non-negative integer $n$ is represented by a python object that holds a unary string of length $n$, and addition is implemented as string concatenation.
I spent a lot of time implementing a Galois class to represent finite fields in my code, and in the process studied the implementation of finite fields via Linear Feedback Shift Registers (LFSR). After that, I decided it might be interesting to use my code to do some data visualizations of the Collatz map, but for a reason I can't fully explain the Sierpinski gasket appeared in the data visualization of my numerical experiment.
You can run the experiment yourself below.
Live Demo: Select "Galois vs. Collatz Comparator" in the sidebar to visualize the Sierpinski gasket hiding in the Collatz map.
If the live demo is asleep you can visit this link to wake it up
The "Missing Modulus" Hypothesis
Instead of dealing directly with the number $n$ in $3n + 1$ I used a known technique of lifting the problem to $P(2)=n$ where $P$ is a polynomial.
Starting from the fact that $3 = 1 + 2$ we have $$(1 + x)P(x) + 1 = 3P(x) + 1$$ when $x=2$. In this expression multiplying $P(x)$ by $x$ is effectively a left shift, whereas dividing $P(x)$ by $x$ is a right shift.
What I noticed is that my representation of the Collatz map in this manner seemed to be like an LFSR implementation of a finite field with a missing modulus. In the LFSR implementation of a finite field, an element of the field is represented as an array of bits which correspond to a polynomial, and multiplication of an element by another element corresponds to polynomial multiplication taken mod $Q(x)$ where $Q(x)$ is an irreducible polynomial. Unlike the case of finite fields, when the Collatz map is represented in polynomial form as I have described, the degree of the polynomial is allowed to grow unbounded.
The $+1$ term in $3n + 1$ effectively induces a non-linear carry propagation, and since I am using a unary number representation system, the entire model seems to be analogous roughly to the Abelian sandpile model.
I thought this was very interesting and have been trying to figure out what it all means.
Galois vs Collatz Comparator
This module runs two maps side-by-side:
- Map A: The standard Collatz map in $\mathbb{Z}$.
- Map B: The perfect Galois orbit in $\mathbb{GF}(2)[x]$, where carries don't exist.
I decided it might be interesting to subtract (in a certain sense) the finite field $\mathbb{F}_2^m$ from the Collatz map, and to my surprise the Sierpinski Gasket appeared, as you can see in the image.
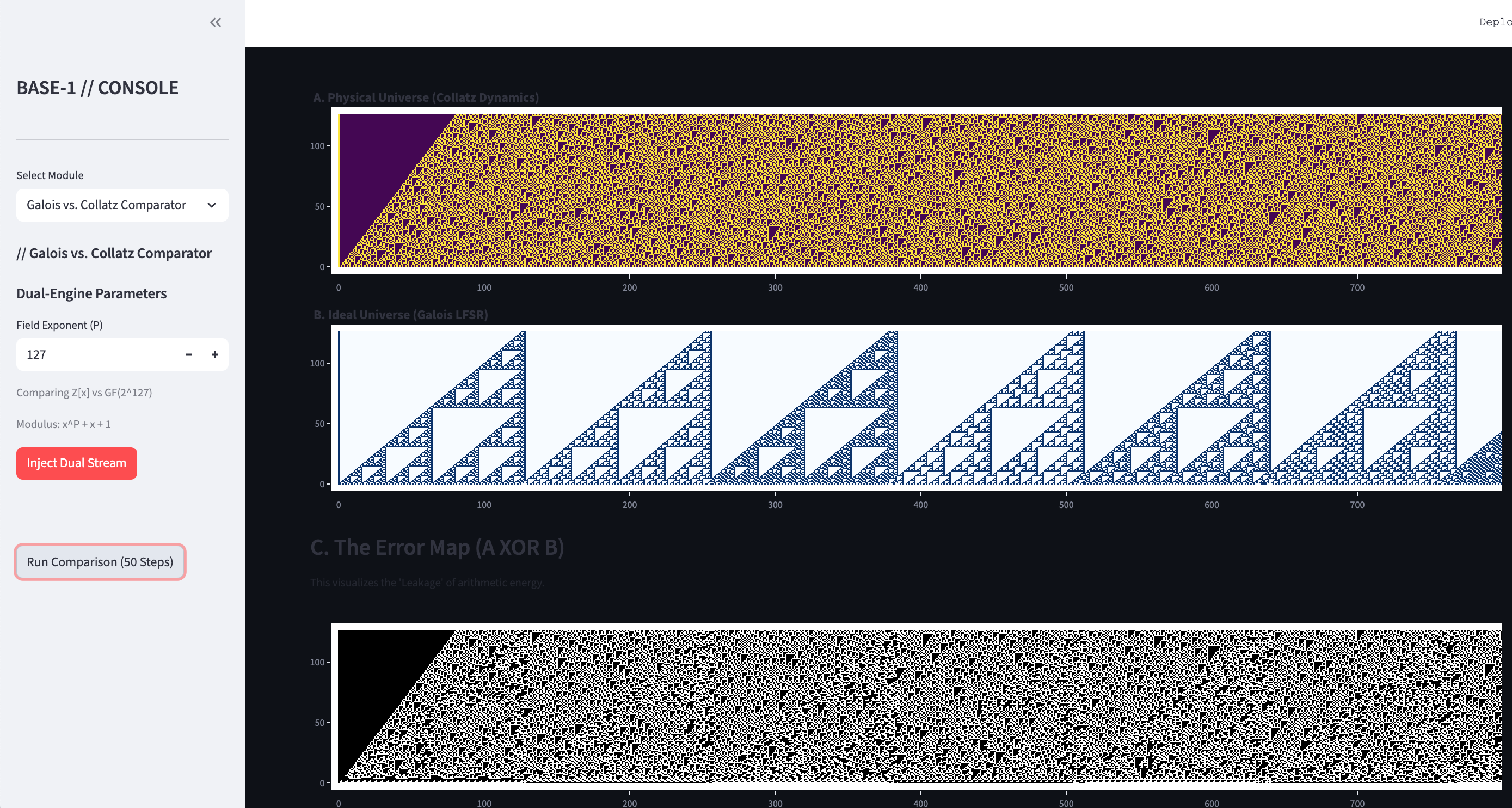
I believe the reason the Sierpinski gasket appears here is directly related to the relationship between finite fields of characteristic 2 and the Sierpinski gasket, but I don't really understand what this relationship is. It's also unclear to me why the Collatz map does not destroy the fractal during the iterations of the map.
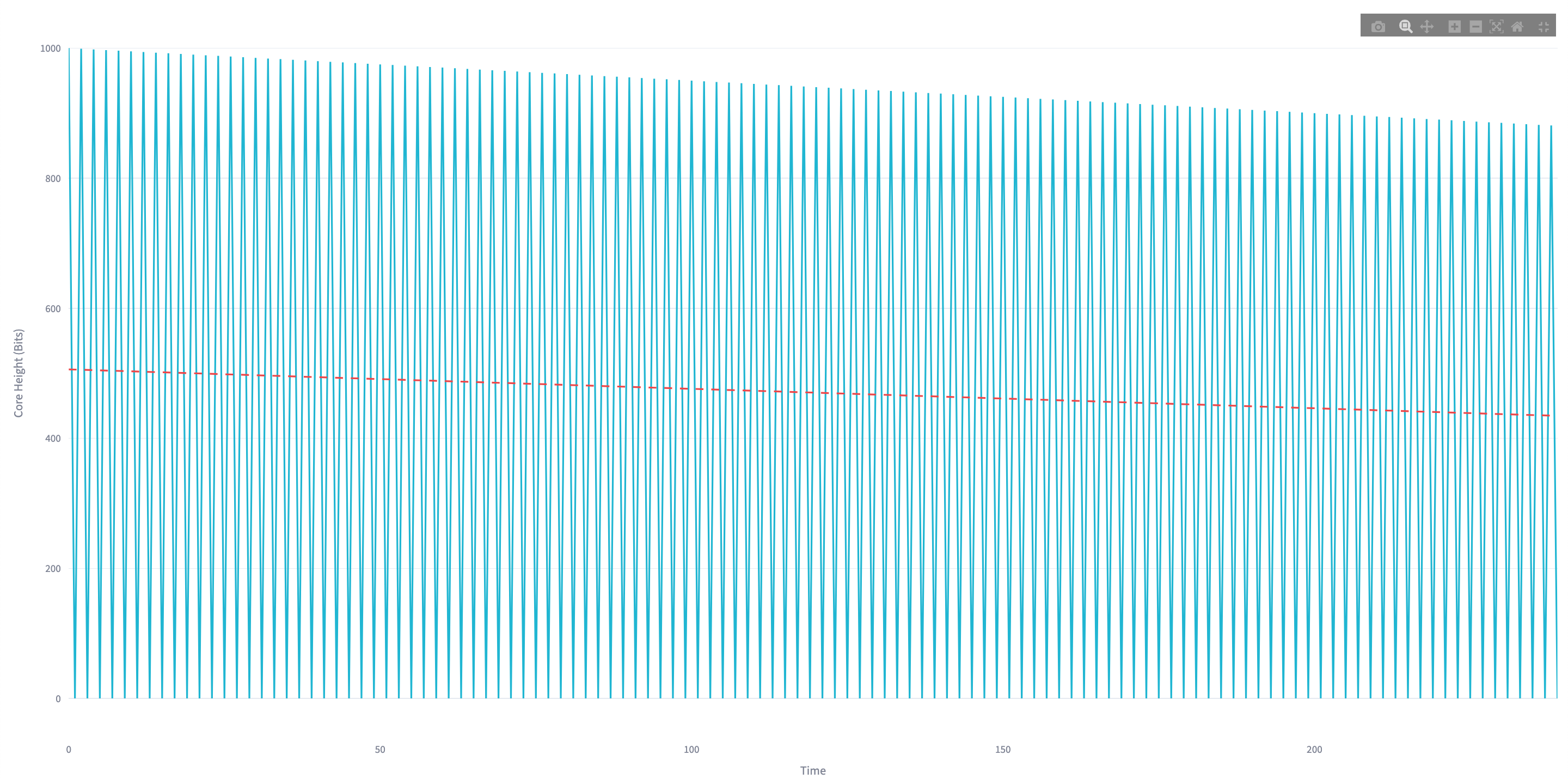
Collatz Resonance Lab
In this module you can inject Mersenne Numbers ($N = 2^k - 1$) into the system to see what would happen. In binary, a Mersenne number consists entirely of 1's.
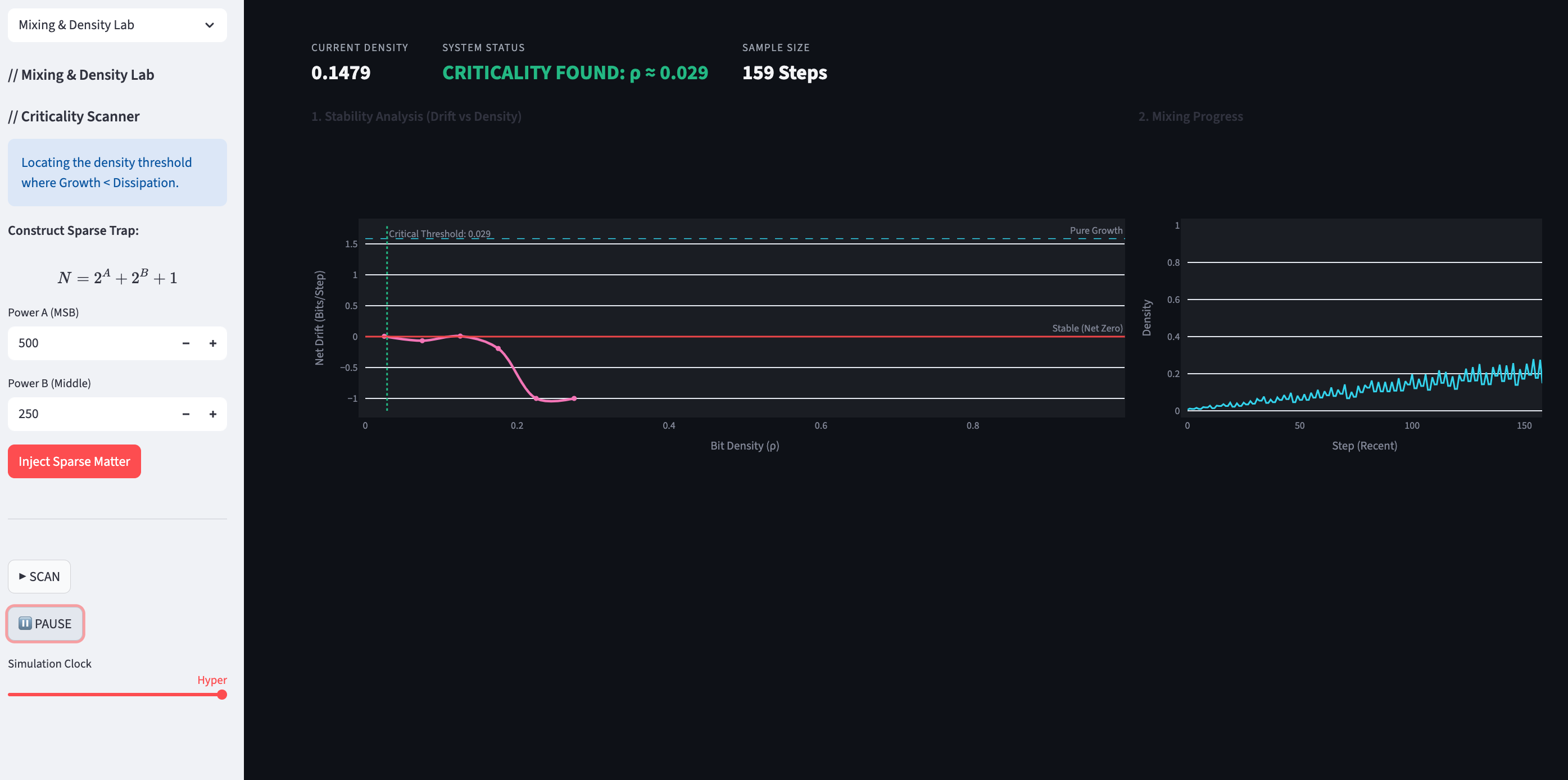
Mixing and Density Lab
This module injects "sparse" numbers like $2^{500} + 2^{250} + 1$, which are the opposite in a certain sense of the Mersenne numbers.