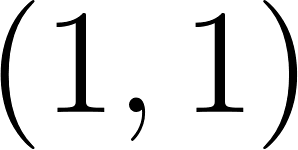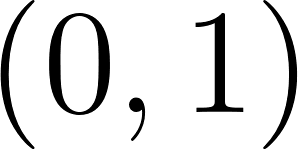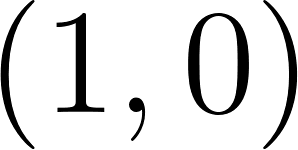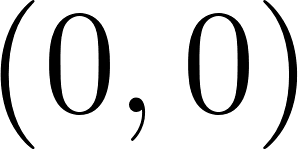19 Nov 2025
Enforcing Mutual Cooperation Through Automation: The GitHub Follower System
Mateo Lafalce - Blog
In this article, we will see how we can enforce mutual cooperation through the automation of certain processes. We will explain how to move from a Nash Equilibrium to a trivial Coordination Game using the GitHub follower system as an example.
Formal Definition of Nash Equilibrium
Let a game be defined by 
players, where each player 
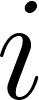has a set of possible strategies 
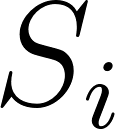and a payoff function 
.
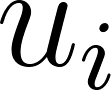A strategy profile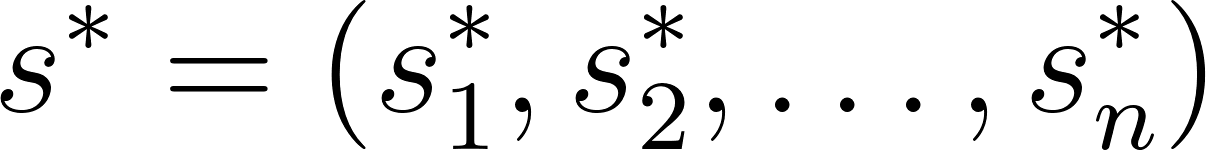 
constitutes a Nash Equilibrium if, and only if, for every player 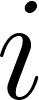and for every alternative strategy 
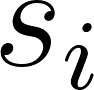belonging to their strategy set 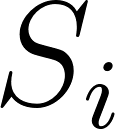, the following inequality holds:
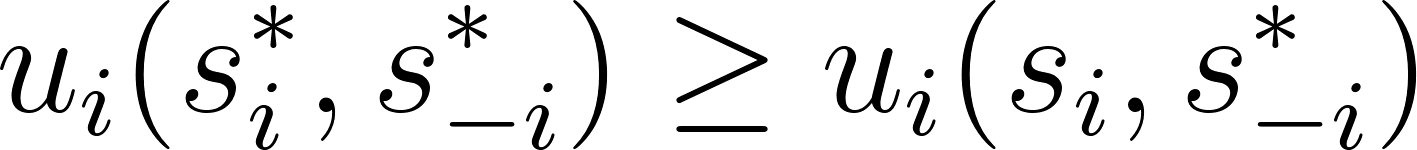
: Is the set of decisions made by all players.
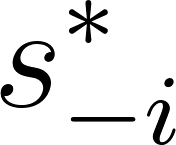: Represents the strategies of all other players except player 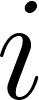. It is what the rest of the world is doing in equilibrium.
vs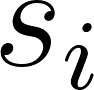
The mathematical inequality tells us:
The utility (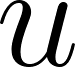
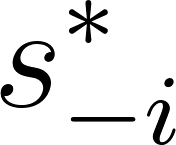) I get playing my equilibrium strategy () given what others do (), is greater than or equal to the utility I would get if I switched my strategy to any other (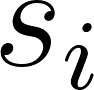), keeping the strategies of others fixed.
The GitHub Case and Its Follower System
Once the Nash equilibrium is defined, let's analyze this particular game:
I will assume that the value of a follow is universally positive (1) and I will also assume that the cost of performing the un/follow action is zero.
If it were a normal simultaneous game, the payoff matrix would look like this:
Me \ Other | Follow ( | No Follow ( |
Follow ( |
|
|
No Follow ( |
|
|
But since my system follows whoever follows me and unfollows whoever unfollows me (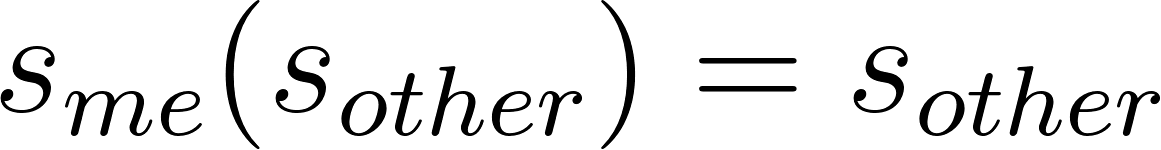
). Therefore, we transform this choice situation into a trivial Coordination Game because the Other player no longer has to worry about “What will I do?” because they know with certainty what the script will do. The payoff would currently look like this:
Other | Follow ( | No Follow ( |
Action ( |
|
|
Forcing mutual cooperation or nothing for anyone, eliminating any possible situation of betrayal or free-riding. My strategy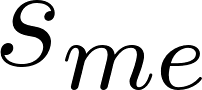 
is not a free variable, it is a function dependent on the other's strategy:
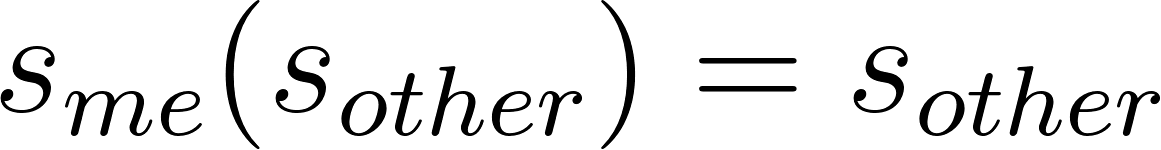
This means that:
Given that 
, the only rational strategy for the other player is to follow me (
). Where both follow each other mutually and gain 1 follower each.
If you want to take a look at the software I have to implement this mutual cooperation logic, here is the link to the repo.
This blog is open source. See an error? Go ahead and propose a change.