Abstract
Lattice-based cryptography (LBC) algorithms are considered suitable candidates for post-quantum cryptography (PQC), as they dominate the standardization process put forward by the National Institute of Standards and Technology (NIST). Indeed, three of the four key encapsulation mechanism (KEM) algorithms in the third round of the process are based on computationally hard lattice problems. On the other hand, there is an urgent need for processor designs that can run PQC algorithms efficiently, especially for embedded systems. This study presents an application-specific instruction set processor (ASIP) design for the Kyber, Saber, and NewHope algorithms based on transport triggered architecture (TTA). Custom hardware accelerators are added to the baseline processor architecture for computation-intensive steps without applying any software optimization to the reference code. We compared FPGA and ASIC implementations of our design with the prominent RISC-V cores and instruction set extension studies in the literature. According to the results, the proposed design offers greater efficiency, better performance, and lower resource utilization than its competitors in most cases.
Similar content being viewed by others
1 Introduction
Cryptography is fundamental to the security of almost every electronic system used today. As our computation techniques and systems have evolved over the years, cryptography has undergone many evolutions to adapt to them. With quantum computer development projects reaching advanced stages in recent years, cryptography faces a new challenge: The widely used public key cryptography algorithms are not secure against quantum computer attacks [1]. Peter Shor showed that the security of public key cryptography algorithms based on integer factorization and discrete logarithm problems could be broken by quantum computing techniques [2]. This means that a sufficiently large quantum computer would pose a severe worldwide security problem. In addition, sensitive information collected today can be stored for future decryption with a quantum computer. For all these reasons, cryptographers have been developing algorithms resistant to quantum and classical computer attacks for some time.
In 2016, NIST started a standardization process to develop cryptography algorithms that could enable secure communication in the quantum age [3]. The aim was not to choose a winning algorithm but to determine alternatives that can be used practically in various fields. The process started with 69 appropriate candidates in the first round. After the evaluations conducted in the second and third rounds, 1 KEM and 3 digital signature algorithms (DSAs) were entitled to be standardized [4, 5]. Kyber is the only algorithm that was standardized as a KEM [6, 7]. Dilithium [8], FALCON [9], and SPHINCS+ [10] were chosen as DSA methods. Currently, the process is being developed to create different KEM alternatives in the fourth round.
LBC refers to cryptographic structures whose security is based on hard problems defined on integer lattices [11]. These methods are used in the most promising algorithms in the NIST PQC Standardization process. In fact, Kyber, Dilithium, and FALCON are built with lattice-based cryptographic structures. In addition, many lattice-based algorithms have been proposed as candidates for both KEM and DSA [4]. This is because the LBC structures provide fast and secure encryption, which makes them the most critical research area for PQC.
While PQC algorithms are being standardized, one of the most critical issues is the development of efficient hardware architectures for them. Creating customized instruction set architectures (ISAs) is essential to ensure these algorithms can be used practically, especially in embedded systems. Loosely coupled hardware accelerators connected to the data buses of processors have many drawbacks, such as data transmission overhead and low flexibility [12]. Extending the instruction sets of general-purpose processors is a classic approach. However, since such cores are not designed for a specific application, achieving the desired efficiency is difficult. In this context, ASIPs can be a good solution due to their highly flexible, customizable, and scalable structure [13]. This structure can meet the low power consumption and high-performance requirements needed in public key cryptography applications.
TTA is an open-source ASIP architecture based on Very Long Instruction Word (VLIW) principles with some improvements [14]. The computation philosophy of TTA is to move data with parallel transport buses between functional units (FUs) where custom instructions reside. TTA-Based Co-Design Environment (TCE) is a fully open-source and royalty-free toolset developed at Tampere University, Finland [15]. It provides various compatible tools for designing, compiling, simulating, debugging, profiling, and generating TTA processors.
In this study, we present a TTA-based ASIP design and custom instructions for three different promising LBC methods: Module Learning With Error (M-LWE) [16], Module Learning With Rounding (M-LWR) [17], and Ring-LWE (R-LWE) [18]. The design is intended for application to KEM algorithms that use these LBC methods and were selected from the second and third round finalists of the NIST PQC Standardization Process: Kyber, Saber [19], and NewHope [20].
The remainder of this work is organized as follows: Sect. 2 discusses related studies and our contributions. Afterward, we briefly introduce the Kyber, Saber, and NewHope algorithms in Sect. 3. Then, Sect. 4 presents the basics of TTA and TCE. In Sect. 5, we explain our designs in detail and evaluate FPGA and ASIC implementations compared with the related studies. Finally, we conclude our work and describe future studies in Sect. 6.
2 Literature Review
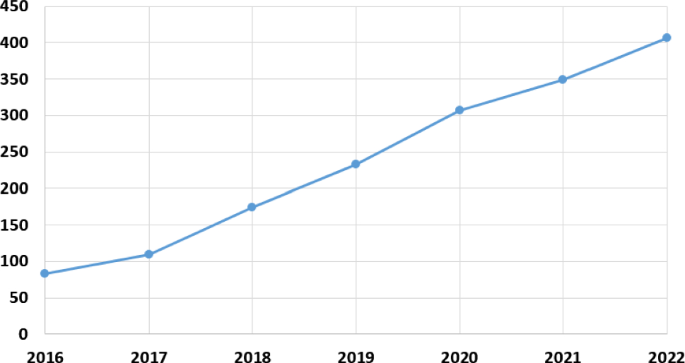
Studies on PQC have been increasing in recent years. Figure 1 demonstrates this trend with data from the Web of Science (WoS) database. Due to the issue’s importance and urgency, this increase can be expected to continue. Bernstein et al. conducted a comprehensive study describing the importance and mathematical background of PQC [11].
Several hardware accelerators were proposed for PQC algorithms in [21,22,23]. In [21], the authors implemented NewHope on low-cost FPGAs. A compact Saber implementation was introduced in [22]. A similar study for Kyber was conducted in [23]. In addition, some studies have proposed hardware accelerators that are loosely coupled to processor cores via buses [24,25,26]. However, such designs have inherent disadvantages, such as high data transfer overhead, strong hardware resource requirements, and low flexibility [12]. In contrast, some studies focus on Number Theoretic Transform (NTT) accelerators to speed up the polynomial multiplications that are extensively performed in most LBC algorithms [7, 25].
Instruction set extension is another approach that has been applied in some PQC hardware studies [12, 27, 28]. This method integrates tightly coupled hardware accelerators into the processor core. In [27], authors used this method for a single encryption scheme. They have extended their work on a RISC-V [29] processor for the other LBC algorithms. A similar study aiming to accelerate Kyber and NewHope was introduced in [28]. They also used an optimized software implementation to support their study. Remarkable acceleration and efficient hardware designs were achieved in both [12, 28].
There are many studies in the literature related to the software implementation of PQC algorithms. Open Quantum Safe is an open-source software library to support the development and prototyping of quantum-resistant cryptography [30]. PQClean is a similar effort to collect clean implementations of KEM and DSA schemes in the NIST project [31]. In addition to these, many studies exist for specific platforms. In [32, 33], the authors developed efficient software for the ARM Cortex-M4 platform targeting embedded systems. Other notable software designed for resource-constrained devices can be found in [34,35,36,37,38].
To the best of our knowledge, there are only a few studies related to TTA-based ASIP design for PQC algorithms [39,40,41]. The authors compared a TTA processor with RISC-V cores for a sample NTRU cryptosystem in [39]. However, this study was based on their own software implementation. In [40], a 64-bit general-purpose TTA processor was proposed. The authors presented results comparing their design with RISC-V rivals on reference PQC software. Thus, they claimed that TTA could be a suitable base ASIP architecture for PQC applications in embedded systems. [41] is the only work in which custom TTA accelerators were proposed for a single PQC scheme.
Our Contributions In this study, we make the following contributions:
-
We present custom TTA operations for three different KEMs based on three LWE variants. These can also be used for similar schemes.
-
We introduce a lightweight ASIP designed with custom TTA operations, especially suitable for PQC applications in embedded systems.
-
We prove the efficiency of our design by comparing it with popular 64-bit RISC-V cores for FPGA and ASIC implementations. We share the comparative PQC test results using reference software.
3 LWE-Based KEMs
This section briefly describes the key generation, encryption, and decryption algorithms of Kyber, Saber, and NewHope KEMs. These schemes are based on some variant of the LWE problem proposed by Regev [18]. In simple terms, the LWE problem relies on the hardness of solving a large number of linear equations, some of which include small errors. Although solving linear equations with Gaussian elimination is easy, this becomes impossible as the number of erroneous samples increases.
3.1 Kyber
Kyber KEM is a part of the Cryptographic Suite for Algebraic Lattices (CRYSTALS) package [42] submitted to the NIST PQC Standardization Process. The other member of this package, Dilithium, is a post-quantum digital signature scheme. Recently, NIST has decided to standardize both Kyber and Dilithium after the evaluations during the third round [5].
The security assumption of the Kyber algorithm relies on the M-LWE problem defined in module lattices. It is a variant of the LWE problem in which polynomial rings are represented with modules [16]. With this method, implementing secure and fast encryption schemes gets easier.
The official Kyber submission package [6] contains an IND-CPA-secure public key encryption scheme called Kyber.CPAPKE. It has several integer parameters for specifying the security level (\(n = 256\), \(q = 3329\), \(k = \left\{ 2; 3; 4\right\} \), \(du = 10\), and \(dv = \left\{ 3; 4; 5\right\} \)). The lattice dimension is determined with nk.
Let the ring \( {\mathbb {Z}}_q [X]/(X^n +1)\) be denoted as \(R_q\). The key generation process is started with a randomly generated matrix \(A \in R^{k \times k} _q\). The vectors \(s, e \in R^k _q\) are sampled with a centered binomial distribution (CBD) by using a pseudo-random function (PRF) [6]. Then, the vector \(t\in R^k _q\) is computed as in Eq. 1. Thus, the vector t is encoded as the public key (pk) and the vector s as the secret key (sk).
$$\begin{aligned} t = A.s + e \end{aligned}$$
(1)
To encrypt a message \(m \in R_q\), the sender first decodes the public key pk to obtain the vector t. Then, a random matrix \(A \in R^{q \times q} _k\) is generated. The vectors \(r, e_1 \in R^k _q\) and \(e_2 \in R_q\) are sampled from a CBD. After that, vectors \(u \in R^n _q\) and \(v \in R_q\) are computed as given in Eq. 2 and Eq. 3. The ciphertext c is encoded from the concatenation of u and v.
$$\begin{aligned}{} & {} u = A^T.r + e_{1} \end{aligned}$$
(2)
$$\begin{aligned}{} & {} v = t^T.r + e_{2} + m \end{aligned}$$
(3)
For decryption, the receiver first decodes ciphertext c to recover the vectors u and v. Finally, the original message m is obtained with the given Eq. 4.
$$\begin{aligned} { m = v - s^T.u} \end{aligned}$$
(4)
Kyber.CCAKEM is the IND-CCA2 secure version of the submission. It is obtained by applying the Fujisaki-Okamoto (FO) transform to Kyber.CPAPKE [43]. IND-CCA2 security is provided with additional hash operations (SHA3-512 and SHA3-256) [6]. In Kyber.CCAKEM, three parameter sets (Kyber512, Kyber768, and Kyber1024) are suggested for NIST security levels 1, 3, and 5, respectively. The formal description of the algorithms and the parameter sets can be found in the specification document [6].
3.2 NewHope
NewHope is an IND-CCA2 secure KEM based on the R-LWE problem defined in polynomial rings. Finite field arithmetic operations are applied to vectors and matrices sampled from a specific polynomial ring. NewHope was one of the fastest algorithms in the NIST PQC Standardization Process. However, it was eliminated in the third round due to its drawbacks compared to Kyber [5].
Both CPA and CCA-secure KEM variants are offered in the NewHope submission package [20]. The FO transform is used to convert CPA-secure schemes to CCA-secure ones. The CPA variants are called NewHope512-CPA-KEM and NewHope1024-CPA-KEM, while the CCA-secure conjugates are NewHope512-CCA-KEM and NewHope1024-CCA-KEM, which match NIST security levels 1 and 5, respectively.
NewHope uses two integer parameters to set the degree of the polynomial ring and the finite field (n, q). The degree is determined according to the security level (\(n = 512\) or \(n = 1024\) ), while the module parameter remains constant (\(q = 12289\)) for both. Another constant parameter (\(k = 8\)) is used to generate noise with the CBD.
Let the ring \( {\mathbb {Z}}_q [X]/(X^n +1)\) be denoted as \(R_q\). A uniformly random polynomial \(a \in R_q\) is generated with a random seed value seed to generate public and secret keys. The vectors \(s \in R_q\) and \(e \in R_q\) are sampled using CBD according to the parameter k. Then, the public key b is computed with Eq. 5 and packed with the seed. The secret key of the receiver is encoded from the vector s.
$$\begin{aligned} { b = a.s + e} \end{aligned}$$
(5)
To encrypt a message \(m \in R_q\), a secret vector \(s'\in R_q\) and error vectors \(e', e''\in R_q\) are sampled with a CBD. After that, the sender computes the vector v and the vector u as given in Eq. 6 and Eq. 7. The ciphertext is then formed as an encoding of the vectors v and u.
$$\begin{aligned} v= & {} b.s' + e'' + m \end{aligned}$$
(6)
$$\begin{aligned} u= & {} a.s' + e' \end{aligned}$$
(7)
In the decryption stage, the vectors v and u are decoded first. The original message m is then obtained with Eq. 8.
$$\begin{aligned} { m = v - u.s} \end{aligned}$$
(8)
The CCA-secure version of NewHope includes additional hash operations originating from the FO transform. Formal descriptions of the algorithms, parameter sets, encoding and decoding functions, and hash operations are accessible from the specification document [20].
3.3 Saber
Saber is an IND-CCA2 secure KEM based on the M-LWR problem. Instead of error generation, a deterministic rounding operation is used in this LWE variant. Thus, fewer random bits are required for encryption and decryption.
Saber was one of the third round finalists of the NIST PQC Standardization Process. The official submission includes CPA and CCA-secure KEMs. Saber uses a CPA-secure public key encryption method called Saber.PKE at its core. The CCA-secure KEM is called Saber.KEM and is obtained by applying the FO transform.
Three parameter sets suggested in the submission are LightSaber, Saber, and FireSaber, which match the NIST security levels 1, 3, and 5, respectively [19]. Constant and variable integer parameters specify the polynomial ring, coefficients, and rounding. The parameters \(n = 256\) and \(q = 2^{13}\) specify the dimensions of the fixed polynomial ring \(R_q = {\mathbb {Z}}_q [X]/(X^n +1)\). Another constant parameter \(p = 2^{10}\) is used as a modulus calculating coefficients in encryption and decryption stages. The variable parameters of the algorithm are module rank parameter l, rounding parameter T, and distribution parameter \(\mu \).
For key generation, a random matrix \(A \in R^{l \times l} _q\) is generated using a PRF (SHAKE-128) with a random seed value \(seed_A\). The secret vector \(s \in R^{l \times 1} _q\) is sampled with a CBD. Then, the vector b is computed as in Eq. 9 with a constant vector \(h \in R^{l \times 1} _q\) used for rounding operations by a simple bit shift. The public key pk is then formed from encoding b and \(seed_A\), while the secret key sk is encoded from vector s.
$$\begin{aligned} { b\equiv (A^T.s + h)\mod q} \end{aligned}$$
(9)
To encrypt a message \(m \in R^{l \times 1} _q\), the sender first rebuilds the matrix A using the public key. Then, the secret vector \(s'\in R^{l \times 1} _q\) is sampled from a CBD. The vectors \(b'\in R^{l \times 1} _p\) and \(v' \in R^{l \times 1} _p \) are computed with Eq. 10 and Eq. 11. The ciphertext c is encoded from the concatenation of vector \(b'\) and \(((v' + m)\mod p)\).
$$\begin{aligned}{} & {} b'\equiv (A.s' + h) \mod q \end{aligned}$$
(10)
$$\begin{aligned}{} & {} v'\equiv b^T. (s'\mod p) \end{aligned}$$
(11)
The receiver uses Eq. 12 for decryption to compute the vector \(v \in R^{l \times 1} _p\). The original message m is then obtained with Eq. 13.
$$\begin{aligned}{} & {} v\equiv b'^T.(s\mod p) \end{aligned}$$
(12)
$$\begin{aligned}{} & {} m\equiv v\mod p \end{aligned}$$
(13)
Similar to Kyber and NewHope, the CCA-secure Saber KEM contains additional hash operations. The authors suggested SHA3-256 and SHA3-512 standards for three different hash stages in the KEM. The specification document provides detailed information about the algorithms, encoding and decoding techniques, hash functions, and more [19].
4 TTA and TCE
In this section, we explain the basic computational approach of TTA. We also briefly introduce TCE, the free and open-source integrated TTA processor design environment.
4.1 TTA
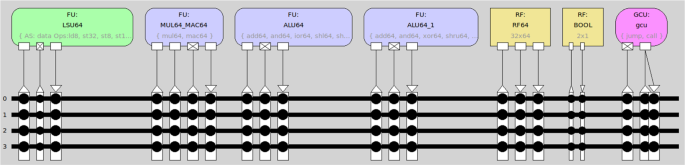
TTA is a processor design concept that prioritizes the advantages of parallel computing. A typical TTA processor consists of FUs, transport buses, and one or more register files. The data to be processed are moved between FUs via transport buses. In other words, computations are just a side effect of data transport in TTA. The related operation in an FU is triggered when the data reach the input ports. After the computation is completed, the result is moved to the following processing location instead of being written to a register file unless necessary. This decreases the register file access rate, which also reduces total energy consumption. The structural model of a typical TTA processor is given in Fig. 2.
TTA processors generally have long instruction words and multiple transport buses. The instruction words contain move slots for each bus that state the FU ports and related operations to be triggered. These operations can be simple instructions such as addition and shifting or more complex functions such as matrix multiplication. The designer determines the content and functionalities of FUs according to the application requirements.
The control unit is actually located as an FU and manages the whole computation process. It fetches the instructions from memory and maintains the program flow with jumps and address counters. The transport buses are connected to FUs via sockets. All the elements that form a TTA processor are highly scalable and customizable. This modular structure is well suited to exploiting instruction-level parallelism (ILP) advantages. All these factors make TTA an ideal template for ASIP designs.
4.2 TCE
TCE is a research project developed and led by the Department of Pervasive Computing at the Tampere University of Technology, Finland [15]. The project aims to create an integrated toolset capable of handling all hardware and software development phases for TTA processors. TCE makes it possible to design highly efficient TTA processors by simply starting with an application code written in a high-level language and a basic architecture definition.
TCE includes several tools with graphical user interfaces to leverage its extensive capabilities easily. The processor design steps in TCE often start with a simple architecture definition file (ADF). The ProDe tool generates a processor model with a convenient interface by reading the base ADF. The designer can make many customizations to this model, such as adding FUs, editing the operations they contain, increasing or decreasing the number of transport buses, and adjusting their widths and connections. The target application is simulated using the cycle-accurate simulator Proxim on the prepared model. It also provides all profiling data, such as the trigger counts of the operations in FUs and the active usage rates of transport buses. Thus, the designer can identify bottlenecks in the system and update the ProDe model. The TTA operations are defined in Operation Set Editor (OSEd). Designers can add their custom operations with OSEd and integrate them into the ProDe model. In this way, the contribution of a concept custom operation can be quickly evaluated with Proxim simulations. After the processor model is developed, hardware description language (HDL) code is generated with the Processor Generator (ProGe) tool. TCE comes with many off-the-shelf hardware implementations by default. The hardware database editor (hdbeditor) organizes both the pre-installed HDL code and the designers’ custom implementations. The HDL code generated with ProGe can then be synthesized in third-party FPGA or ASIC platforms. The entire processor design procedure with TCE is summarized in Fig. 3.
In TTA, the compiler has a critical role, as the scheduling is done statically at compile time according to the processor architecture. TCE contains an LLVM-based retargetable compiler responsible for executable code generation. The TCE compiler (tcecc) takes ADF and high-level application code as inputs and produces the executable binary code.
5 ASIP Design for PQC
In this section, we introduce our ASIP designs and share detailed test results obtained from reference PQC software. In addition, we explain our custom operation determination technique, balanced design approach, and future research scope with a gap analysis.
We chose TTA as our ASIP design method. Since the lattice-based PQC algorithms involve many computations that can be executed in parallel, we intended to take advantage of the ILP. In addition, TTA and TCE are the only options to provide open-source and free ASIP architecture and development environment.
5.1 Base Processor Design
TCE tools had stable 32-bit support at the time of this study. However, this was not yet the case for 64-bit tools. In this study, we use reference PQC software from the PQClean project, which contains many operations on 64-bit data [31]. Therefore, we made some changes and arrangements to the open-source TCE source code, as we explained in detail in our previous work [41]. Then, we designed and implemented a 64-bit general-purpose TTA processor, which we call TTA64, using the basic operations (AND, OR, ADD, SHIFT, MUL, etc.) defined in the standard operation set. In [41], we compared the TTA64 with popular 64-bit RISC-V processors (Rocket Core [44] and CVA6 [45]) in many ways, demonstrating that it may be a suitable ASIP design for PQC applications in embedded systems. In this study, we used the most efficient configuration of TTA64 with four transport buses as the base core architecture, with which we later integrated custom operations. The structural ProDe model of TTA64 is presented in Fig. 4. In Table 1, we compare clock cycle counts for the CCA2-secure versions of the Kyber, NewHope, and Saber KEMs on TTA64 and RISC-V cores. The numbers represent the total execution cycles required for the key generation, encapsulation, and decapsulation stages for the standard parameter sets defined in the related KEM specifications.
5.2 Custom TTA Operations
TTA is an architecture that facilitates processor customization. Leveraging this vital aspect of TTA, we designed and implemented several custom operations for the Kyber, NewHope, and Saber KEMs to achieve higher performance and energy efficiency. It is possible to design and integrate many or complex operations in VLIW-type architectures such as TTA. However, we preferred a balanced design approach in this study. We aimed to increase performance without excessively enlarging the required chip area or reducing the clock frequency. Thus, we achieved high energy efficiency with relatively simple and few custom operations.
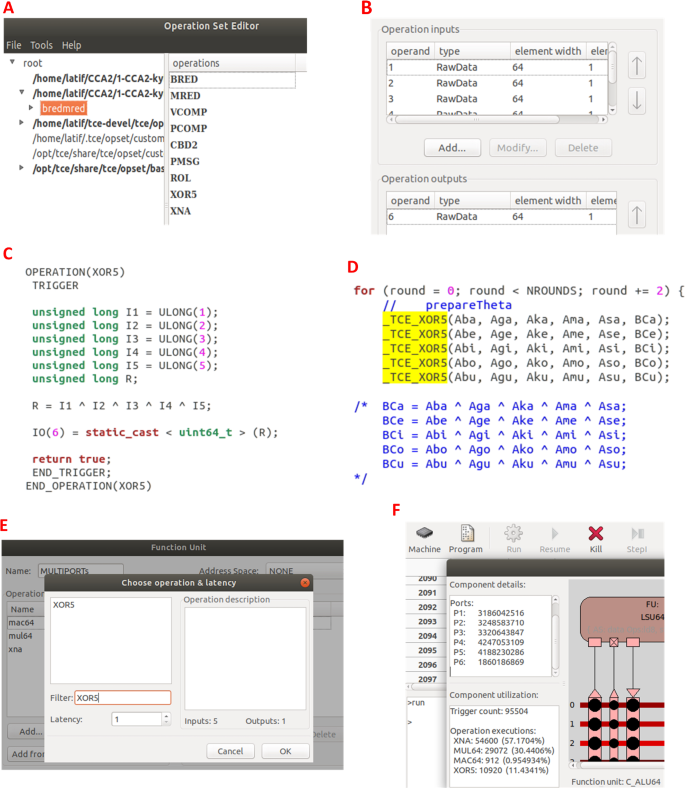
The operation set of a TTA processor is managed by the Operational Set Editor (OSEd) tool available in TCE [15]. After thoroughly examining the PQClean codes and identifying custom operation candidates, we added them to the TTA64 operation set with the OSEd. The process of integrating custom operations into the TCE tools and compilation chain is presented in Fig. 5. The first step is to define the name of the operation to be added to the OSEd tool and its properties, such as the number of input and output ports and data types. Then, a C++ code block expressing the behavior of the operation is written and compiled. Next, the operation is added to the relevant software code using the in-line assembly method, replacing the part it is intended for. This step enables the custom operation to be recognized in the ProDe tool so that it can be added to a processor model. Finally, the TCE compiler compiles the ADF file containing the processor design and the software containing custom operations to produce executable code. The Proxim tool is then used to simulate the processor model with the compiled code in a cycle-accurate manner to verify that the operation works correctly.
We performed profiling analyses with the Proxim simulator to integrate the custom operations to the FUs to determine the best performance. Many candidate operations were put through this test cycle with various scenarios. As a result, operations that increase efficiency under our balanced design approach were implemented using VHDL. We give the functionalities of the custom operations developed for Kyber in Table 2. We also give the latency of these instructions in terms of clock cycles and their relevant code blocks in the PQClean library in Table 3. We provide the same information for NewHope KEM in Tables 4 and 5. Similarly, custom Saber operations are detailed in Tables 6 and 7. The terms C and C1-C5 represent constant values defined in the related algorithm specifications, while the terms IN, IN1-IN5, and O express the input and output ports of the custom operations, respectively. Since the algorithms use the same Keccak functions, some operations are identical for the three KEMs.
The MRED operation converts a 32-bit input to a 16-bit congruent output using the Montgomery modular reduction algorithm [46]. Similarly, the BRED operation calculates the centered representative congruent value of a 16-bit input value using the Barrett modular reduction method [46]. The CBD2 operation accelerates the computation of polynomial coefficients from a uniformly random array following the centered binomial distribution. The PCOMP operation maps polynomial coefficients to positive standard exponents. The VCOMP operation is a combination of the polynomial vector compression operations. On the other hand, the ROL, XOR5, and XNA operations are used in the Keccak state permutations.
The MREDNH and PCMPNH operations are the adoptions of the MRED and PCOMP operations to the NewHope KEM. The CFREE operation performs constant time fully modular reduction of 16-bit input values except the first modulo operation. The RDPRM operation operates as the parameter reduction function in both odd and even stages of NTT calculations. As the name suggests, the HAMW operation computes the Hamming weight [47] of given coefficients in the sampling of polynomials. The PTMNH operation is used in message encoding to speed up the conversion of polynomials.
Custom operation definition process in TCE: A) Introducing the operation to the OSEd, B) Determining the operation properties, C) Definition of the operation behavior, D) Integrating the operation into the software, E) Adding operation to the processor model in ProDe, F) Cycle-accurate simulation in Proxim
SHANDLS1 and SHANDLS1 operations combine the frequently repeated right shift and AND operations in the centered binomial distribution function. The SUB3 is a simple triple subtraction operation that resides in the interpolation and second stages of the Karatsuba multiplication algorithm [48]. Similarly, the EVALR4 operation is used in the evaluation phase of the Toom-Cook multiplication algorithm [48]. The ROUND operation performs the rounding operation on the polynomial coefficients according to the constraints defined in the Saber KEM specifications.
5.3 Design of the Custom Processors
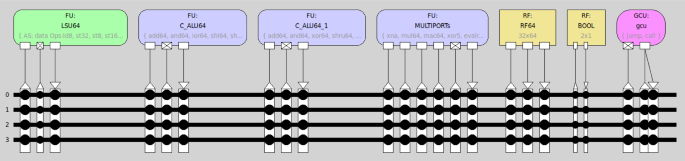
We designed and implemented custom TTA processors for the Kyber, NewHope, and Saber KEMs, integrating the custom operations into the TTA64 processor. We used the same processor model to create a custom core, which we call C-TTA64, that can accelerate all three algorithms. Figure 6 illustrates the structural design of the C-TTA64 processor in the ProDe environment.
Using the same C-TTA64 model, we also developed Custom Kyber, Custom NewHope, and Custom Saber processors that include custom operations only for the relevant algorithm. The distribution of custom operations to the FUs in the relevant C-TTA64 core is given in Table 8. The operations with more than two input ports are placed in the MULTIPORTs FU. The multiply (mul) and multiply-and-accumulate (mac) operations from the TTA64 processor are located in the same unit. The C_ALU64 and C_ALU64_1 FUs contain general-purpose operations given in [41] together with the custom operations. All operations were developed to be compatible with the 64-bit transport bus structure. We used a fully connected bus architecture as there were some compile time issues with the other options in the 64-bit version of the TCE toolset.
All FUs were implemented in VHDL and added to the hardware database of the tool using HDB Editor [15]. Then, we generated the synthesizable HDL implementation of our custom processors along with the control unit and data buses. After that, we performed behavioral simulations in Xilinx Vivado (version 2018.2) [49] with the testbench automatically generated by the ProGe tool. We shared all software and hardware designs developed in this study as open-source code on GitHub.Footnote 1
5.4 Tests and Results
We performed PQClean tests on our custom processor and obtained the total number of clock cycles for the key generation, encapsulation, and decapsulation stages. Then, we compared the results with the existing studies in the literature that are suitable for low-power embedded systems. As can be seen from Table 9, our design outperforms the ARM Cortex-M0 [32] core, even when some software optimizations are used [33]. We also obtained better results than [28], in which the VexRiscv core with custom PQC instructions runs optimized software. It should be noted that we do not apply any optimization to the PQClean software in this study. Compared with TTA64, the performance improvement is approximately 50% for Kyber and 25% for NewHope. However, the difference in acceleration rate is around 10% for Saber. On the other hand, our results slightly fall behind the state-of-the-art [12] in terms of the total number of clock cycles alone.
We chose the Xilinx Artix-7 [50] platform for FPGA implementation to make a meaningful comparison with the related works. In Table 10, we show the synthesis results of our designs obtained from Vivado with the default synthesis settings. We compare the FPGA resources with the CVA6 and ROCKET cores (both of which implement RV64GC [29]) and RISC-V instruction set extension studies for PQC. We achieve resource utilization values that are similar to those of the CVA6 and ROCKET cores while providing much better performance, as shown in Tables 1 and 9. We also obtained higher clock frequencies and at least 2.1X smaller chip areas than the state of the art [12]. On the other hand, although [28] has lower FPGA resource requirements, our custom processors are superior in terms of performance.
We made another comparison regarding total energy consumption. In Table 11, we present the results calculated from the energy equation given in 14, where E, P, t, CC, and \(f_{max}\) express energy, power, execution time, cycle count, and maximum clock frequency, respectively. The power values were obtained from the Vivado Power Analyzer. This was achieved by generating synthesis activity files (SAIF) from the post-synthesis simulation of all PQClean tests for each core. The results clearly prove that both TTA64 and C-TTA64 consume at least 2\(\times \) less energy than the 64-bit RISC-V cores. The difference between our designs indicates the efficiency of the custom operations. However, since we cannot accelerate Saber as much as other KEMs, there is no significant difference in total energy consumption between the two cores.
$$\begin{aligned} E(t) = P \times t = P \times \text {CC}\times \frac{1}{ f_{max}} \end{aligned}$$
(14)
We also analyzed our designs for ASIC implementation. We show the synthesis results of our cores for TSMC 40nm technology in Table 12. The only study that has reported ASIC results is [12]. The authors state that their design can run at 45.47 MHz clock frequency in the UMC 65nm process. However, they report the chip area, cell count, and power values for 10 MHz frequency. The power consumption of our custom processors is in the range of 0.4–0.8 mW when synthesized at that frequency. In addition, the maximum clock frequency value we obtained for our custom cores at the highest effort level of the Genus [52] tool was 135 MHz. On the other hand, our C-TTA64 core occupies a 3.8\(\times \) smaller chip area than that of [12] while also providing a 10\(\times \) faster clock frequency. Since the underlying ASIC technologies are different, considering the total cell count would be a more accurate approach. When analyzed from this perspective, it is seen that C-TTA64 requires 2x fewer cell resources. When the total energy consumption is analyzed using the values given in Tables 9 and 12, it can be concluded that our C-TTA64 processor is more efficient for Kyber and Saber but less efficient for NewHope than its competitor.
5.5 Future Research Scope
LBC methods play a critical role in studies on developing KEM and DSA methods resistant to quantum computer attacks. Various hardware and software studies for Kyber, NewHope, and Saber KEMs are in the literature. Instruction set extension studies were also proposed for these methods on RISC processors. However, there are still very few ASIP studies available. Lattice-based PQC algorithms are very suitable for ILP since they involve calculations that can be executed simultaneously. Therefore, TTA has serious potential for efficiently accelerating PQC algorithms. In addition, open-source and free development tools such as TCE offer valuable opportunities for designers. Thus, it can be predicted that TTA and TCE will be more prominent in future studies.
We adopted a balanced design approach and implemented a few custom hardware operations by combining certain computations from the software implementation. This helped us achieve higher performance than the related studies. We did not utilize various NTT methods [53] or optimized modular arithmetic optimizations such as Plantard [54] in this work. However, custom operation designs based on these methods could lead to much higher performance and more efficient ASIP designs in future studies. Another improvement that could be made in future studies is to evaluate the TTA architecture and our custom operations against power side-channel attacks. Conducting studies on this subject in the near future will be valuable in improving ASIP architectures for PQC. Developing a stable 64-bit version of the TCE toolset and investigating optimized bus architectures instead of a fully connected transport bus structure could also be research progressive topics.
6 Conclusion
Quantum computers are likely to be used practically in the near future. This technological leap is expected to bring invaluable benefits to humanity. However, the computational capabilities of quantum computers pose a serious threat to widely used public key cryptography systems. Researchers have been focusing on quantum-safe cryptography methods in recent years. In that regard, lattice-based schemes promise a faster and more reliable basis for PQC compared to other fields. LBC algorithms dominate the NIST PQC Standardization Process. In this study, we designed and implemented custom TTA operations for accelerating Kyber, NewHope, and Saber KEMs based on three different lattice-based hard problems. Due to our design strategy, we preferred fewer and simpler operations over more or complex instructions. Then, we integrated the operations into a 64-bit general-purpose TTA core developed in our previous study [41]. The entire design was implemented in VHDL and then synthesized for FPGA and ASIC. The PQClean library was used for tests without applying software optimization. We compared our design with the popular 64-bit RISC-V cores and the instruction set extension studies targeting low-power embedded systems. We provided comparative tables that present the resource utilization, cycle count, and energy consumption of all cores for all KEM parameter sets. We explained the advantages and disadvantages of our designs compared to designs from related studies. Finally, we proposed a scalable, fast, and efficient ASIP design that can be further improved. In future studies, we plan to develop custom operations and core designs for lattice-based digital signature schemes.
Notes
References
Micciancio, D.; Regev, O.: In: Bernstein, D.J.; Buchmann, J.; Dahmen, E. (eds.) Post-Quantum Cryptography, Lattice-Based Cryptography, pp. 147–191. Springer, Berlin (2009). https://doi.org/10.1007/978-3-540-88702-7_5
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th Annual Symposium on Foundations of Computer Science, pp. 124– 134 (1994). https://doi.org/10.1109/SFCS.1994.365700
Alagic, G.; Alperin-Sheriff, J.; Apon, D.; Cooper, D.; Dang, Q.; Miller, C.; Moody, D.; Peralta, R.; Perlner, R.; Robinson, A.; Smith-Tone, D.; Liu, Y.-K.: Status Report on the First Round of the NIST Post-Quantum Cryptography Standardization Process. NIST Interagency/Internal Report (NISTIR). National Institute of Standards and Technology, Gaithersburg (2019). https://doi.org/10.6028/NIST.IR.8240
Moody, D.; Alagic, G.; Apon, D.; Cooper, D.; Dang, Q.; Kelsey, J.; Liu, Y.-K.; Miller, C.; Peralta, R.; Perlner, R.; Robinson, A.; Smith-Tone, D.; Alperin-Sheriff, J.: Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process. NIST Interagency/Internal Report (NISTIR). National Institute of Standards and Technology, Gaithersburg (2020). https://doi.org/10.6028/NIST.IR.8309
Alagic, G.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.M.; Lichtinger, J.; Liu, Y.-K.; Miller, C.A.; Moody, D.; Peralta, R.; Perlner, R.; Robinson, A.; Smith-Tone, D.; Apon, D.: Status Report on the Third Round of the NIST Post-Quantum Cryptography Standardization Process. NIST Interagency/Internal Report (NISTIR). National Institute of Standards and Technology, Gaithersburg (2022). https://doi.org/10.6028/NIST.IR.8413
Avanzi, R.M.; Bos, J.W.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D.: CRYSTALS-Kyber Algorithm Specifications And Supporting Documentation (version 2.0) (2019). https://api.semanticscholar.org/CorpusID:231601974
Nguyen, H.; Tran, L.: Design of polynomial ntt and intt accelerator for post-quantum cryptography crystals-kyber. Arab. J. Sci. Eng. 48(2), 1527–1536 (2023)
Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D.: Crystals-dilithium: a lattice-based digital signature scheme. IACR Trans. Cryptogr. Hardw. Embed. Syst. 8, 238–268 (2018)
Fouque, P.-A.; Hoffstein, J.; Kirchner, P.; Lyubashevsky, V.; Pornin, T.; Prest, T.; Ricosset, T.; Seiler, G.; Whyte, W.; Zhang, Z.; et al.: Falcon: fast-Fourier lattice-based compact signatures over NTRU (2018). https://www.di.ens.fr/texttildelow prest/Publications/falcon.pdf
Bernstein, D.J.; Hülsing, A.; Kölbl, S.; Niederhagen, R.; Rijneveld, J.; Schwabe, P.: The sphincs+ signature framework. In: Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, pp. 2129–2146 ( 2019)
Bernstein, D.J.; Lange, T.: Post-quantum cryptography. Nature 549, 188–194 (2017). https://doi.org/10.1038/nature23461
Fritzmann, T.; Sigl, G.; Sepúlveda, J.: Risq-v: tightly coupled risc-v accelerators for post-quantum cryptography. IACR Trans. Cryptogr. Hardw. Embed. Syst. 8, 239–280 (2020)
Keutzer, K.; Malik, S.; Newton, A.R.: From asic to asip: the next design discontinuity. In: Proceedings. IEEE International Conference on Computer Design: VLSI in Computers and Processors, pp. 84–90 (2002). https://doi.org/10.1109/ICCD.2002.1106752
Corporaal, H.: Microprocessor Architectures: from VLIW to TTA. Wiley, Chichester (1997)
Jääskeläinen, P.; Viitanen, T.; Takala, J.; Berg, H.: In: Hussain, W.; Nurmi, J.; Isoaho, J.; Garzia, F. (eds.) HW/SW Co-design Toolset for Customization of Exposed Datapath Processors, pp. 147–164. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-49679-5_8
Langlois, A.; Stehlé, D.: Worst-case to average-case reductions for module lattices. Des. Codes Crypt. 75(3), 565–599 (2015)
Banerjee, A.; Peikert, C.; Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) Advances in Cryptology-EUROCRYPT 2012, pp. 719–737. Springer, Berlin (2012)
Lyubashevsky, V.; Peikert, C.; Regev, O.: On ideal lattices and learning with errors over rings. In: Annual International Conference on the Theory and Applications of Cryptographic Techniques, pp. 1–23. Springer (2010)
D’Anvers, J.-P.; Karmakar, A.; Roy, S.S.; Vercauteren, F.; Mera, J.M.B.; Van Beirendonck, M.; Basso, A.: SABER: Mod-LWR based KEM (Round 3 Submission) (2020). www.esat.kuleuven.be/cosic/pqcrypto/saber/files/saberspecround3.pdf
Alkım, E.; Avanzi, R.M.; Bos, J.W.; Ducas, L.; de la Piedra, A.; Pöppelmann, T.; Schwabe, P.; Stebila, D.; Albrecht, M.R.; Orsini, E.; Osheter, V.; Paterson, K.G.; Peer, G.; Smart, N.P.: NEWHOPE algorithm specification and supporting document (2019). https://newhopecrypto.org/data/NewHope-2019-07-10.pdf
Oder, T.; Güneysu, T.: Implementing the newhope-simple key exchange on low-cost fpgas. In: Progress in Cryptology—LATINCRYPT 2017: 5th International Conference on Cryptology and Information Security in Latin America, Havana, Cuba, September 20–22, 2017, Revised Selected Papers 5, pp. 128–142 (2019). Springer
Mera, J.M.B.; Turan, F.; Karmakar, A.; Roy, S.S.; Verbauwhede, I.: Compact domain-specific co-processor for accelerating module lattice-based kem. In: 2020 57th ACM/IEEE Design Automation Conference (DAC), pp. 1–6 (2020). IEEE
Xing, Y.; Li, S.: A compact hardware implementation of cca-secure key exchange mechanism crystals-kyber on fpga. IACR Trans. Cryptogr. Hardw. Embed. Syst. 5, 328–356 (2021)
Fritzmann, T.; Sharif, U.; Müller-Gritschneder, D.; Reinbrecht, C.; Schlichtmann, U.; Sepúlveda, J.: Towards reliable and secure post-quantum co-processors based on risc-v. In: 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), pp. 1148–1153 (2019). IEEE
Banerjee, U.; Ukyab, T.S.; Chandrakasan, A.P.: Sapphire: a configurable crypto-processor for post-quantum lattice-based protocols (2019). arXiv preprint arXiv:1910.07557
Wang, W.; Jungk, B.; Wälde, J.; Deng, S.; Gupta, N.; Szefer, J.; Niederhagen, R.: Xmss and embedded systems: Xmss hardware accelerators for risc-v. In: International Conference on Selected Areas in Cryptography, pp. 523–550. Springer (2019)
Fritzmann, T.; Sigl, G.; Sepúlveda, J.: Extending the risc-v instruction set for hardware acceleration of the post-quantum scheme lac. In: 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), pp. 1420–1425. IEEE (2020)
Alkim, E.; Evkan, H.; Lahr, N.; Niederhagen, R.; Petri, R.: Isa extensions for finite field arithmetic. IACR Trans. Cryptogr. Hardw. Embed. Syst. 20, 219–242 (2020)
Asanović, K.; Patterson, D.A.: Instruction sets should be free: the case for risc-v. Tech. Rep. UCB/EECS-2014-146. EECS Department, University of California, Berkeley (2014)
Stebila, D.; Mosca, M.: Post-quantum key exchange for the internet and the open quantum safe project. In: International Conference on Selected Areas in Cryptography, pp. 14–37. Springer (2016)
Kannwischer, M.J.; Schwabe, P.; Stebila, D.; Wiggers, T.: Improving software quality in cryptography standardization projects. In: IEEE European Symposium on Security and Privacy, EuroS &P 2022-Workshops, Genoa, Italy, June 6–10, 2022, pp. 19– 30. IEEE Computer Society, Los Alamitos ( 2022). https://doi.org/10.1109/EuroSPW55150.2022.00010
Kannwischer, M.J.; Rijneveld, J.; Schwabe, P.; Stoffelen, K.: pqm4: testing and benchmarking nist pqc on arm cortex-m4 (2019)
Alkim, E.; Bilgin, Y.A.; Cenk, M.; Gérard, F.: Cortex-m4 optimizations for \(\{\)R, M\(\}\) lwe schemes. IACR Trans. Cryptogr. Hardw. Embed. Syst. 6, 336–357 (2020)
Liu, Z.; Pöppelmann, T.; Oder, T.; Seo, H.; Roy, S.S.; Güneysu, T.; Großschädl, J.; Kim, H.; Verbauwhede, I.: High-performance ideal lattice-based cryptography on 8-bit avr microcontrollers. ACM Trans. Embed. Comput. Syst. 16(4), 1–24 (2017)
Boorghany, A.; Sarmadi, S.B.; Jalili, R.: On constrained implementation of lattice-based cryptographic primitives and schemes on smart cards. ACM Trans. Embed. Comput. Syst. 14(3), 1–25 (2015)
Kumari, S.; Singh, M.; Singh, R.; Tewari, H.: To secure the communication in powerful internet of things using innovative post-quantum cryptographic method. Arab. J. Sci. Eng. (2022). https://doi.org/10.1007/s13369-021-06166-6
Al-Saggaf, A.A.; Sheltami, T.; Alkhzaimi, H.; Ahmed, G.: Lightweight two-factor-based user authentication protocol for iot-enabled healthcare ecosystem in quantum computing. Arab. J. Sci. Eng. 48(2), 2347–2357 (2023). https://doi.org/10.1007/s13369-022-07235-0
Babu, J.; Padmavathy, R.; et al.: Quantum-secure n2n authentication protocol model for iot sensor networks. Arab. J. Sci. Eng. (2023). https://doi.org/10.1007/s13369-023-08242-5
Akcay, L.; YALÇIN, S.B.Ö.: Comparison of risc-v and transport triggered architectures for a postquantum cryptography application. Turk. J. Electr. Eng. Comput. Sci. 29(1), 321–333 (2021)
Akcay, L.; Ors, B.: Custom tta operations for accelerating kyber algorithm. In: 2021 13th International Conference on Electrical and Electronics Engineering (ELECO), pp. 455–459. IEEE (2021)
Akçay, L.; Yalçın, B.Ö.: Analysing the potential of transport triggered architecture for lattice-based cryptography algorithms. Int. J. Embed. Syst. 15(5), 404–420 (2022)
Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Stehle, D.: Crystals-kyber: a cca-secure module-lattice-based kem. In: 2018 IEEE European Symposium on Security and Privacy (EuroS P), pp. 353–367 (2018). https://doi.org/10.1109/EuroSP.2018.00032
Fujisaki, E.; Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2013)
Asanovic, K.; Avizienis, R.; Bachrach, J.; Beamer, S.; Biancolin, D.; Celio, C.; Koenig, J.: The rocket chip generator. Technical report (2016)
Zaruba, F.; Benini, L.: The cost of application-class processing: energy and performance analysis of a linux-ready 1.7-ghz 64-bit risc-v core in 22-nm fdsoi technology. IEEE Trans. Very Large Scale Integr. VLSI Syst. 27(11), 2629–2640 (2019). https://doi.org/10.1109/TVLSI.2019.2926114
Knezevic, M.; Vercauteren, F.; Verbauwhede, I.: Faster interleaved modular multiplication based on barrett and montgomery reduction methods. IEEE Trans. Comput. 59(12), 1715–1721 (2010). https://doi.org/10.1109/TC.2010.93
Wei, V.K.: Generalized hamming weights for linear codes. IEEE Trans. Inf. Theory 37(5), 1412–1418 (1991). https://doi.org/10.1109/18.133259
Allam, H.P.; Mandal, S.; Roy, D.B.: A comparative analysis between karatsuba, toom-cook and ntt multiplier for polynomial multiplication in ntru on fpga. In: 2023 Asian Hardware Oriented Security and Trust Symposium (AsianHOST), pp. 1–6 (2023). https://doi.org/10.1109/AsianHOST59942.2023.10409344
Vivado Design Suite User Guide. AMD Documentation Portal (2023). https://docs.xilinx.com/r/en-US/ug910-vivado-getting-started/Vivado-Design-Suite-Overview
Przybus, B.: Xilinx redefines power, performance, and design productivity with three new 28 nm fpga families: Virtex-7, kintex-7, and artix-7 devices. Xilinx White Paper (2010). https://mikrokontroler.pl/wp-content/uploads/pliki/wp373_V7_K7_A7_Devices.pdf
Traber, A.; Zaruba, F.; Stucki, S.; Pullini, A.; Haugou, G.; Flamand, E.; Gurkaynak, F.K.; Benini, L.: Pulpino: a small single-core risc-v soc. In: 3rd RISCV Workshop (2016)
Deshpande, N.; Sowmya, K.: A review on asic synthesis flow employing two industry standard tools. Int. J. Eng. Res. Technol. 8(17), 25 (2020)
Zhang, C.; Liu, D.; Liu, X.; Zou, X.; Niu, G.; Liu, B.; Jiang, Q.: Towards efficient hardware implementation of ntt for kyber on fpgas. In: 2021 IEEE International Symposium on Circuits and Systems (ISCAS), pp. 1–5 (2021). https://doi.org/10.1109/ISCAS51556.2021.9401170
Huang, J.; Zhang, J.; Zhao, H.; Liu, Z.; Cheung, R.C.; Koç, Ç.K.; Chen, D.: Improved plantard arithmetic for lattice-based cryptography. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2022(4), 614–636 (2022)
Acknowledgements
We thank the TCE team for supporting this work and their efforts to improve the toolset.
Funding
Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK).
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Akçay, L., Yalçın, B.Ö. Lightweight ASIP Design for Lattice-Based Post-quantum Cryptography Algorithms. Arab J Sci Eng 50, 835–849 (2025). https://doi.org/10.1007/s13369-024-08976-w
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1007/s13369-024-08976-w