LEV-1 is a small lunar hopper that was carried by the SLIM lunar lander. It was released a few metres above the surface on January 19, as part of the lunar landing of SLIM. LEV-1 transmits telemetry in the 435 MHz amateur satellite band (it has an IARU satellite coordination approval), and also in S-band. Shortly after the landing, CAMRAS received the 437.410 MHz signal from LEV-1 using the 25 m radiotelescope at Dwingeloo. They have published a couple of IQ recordings in their directory of miscellaneous recordings (see the filenames starting by slim_).
The information about the telemetry signal of LEV-1 is scarce. Its website just says
Telemetry format of LEV-1 stands on CCSDS. The contents of telemetry are under developing.
The IARU coordination sheet contains other clues, such as the mention of PCM/PSK/PM, CW, and bitrates of 31, 31.25 and 32 bps, but not much else. Regardless of the mention of CCSDS, I have found that the signal from LEV-1 is quite peculiar. This post is an account of my attempt to decode the data.
In this post I will only be looking at the file slim_2024-01-19_15_39_58_437.200MHz_1.00Msps_ci16_le.chan0.sigmf-meta. I guess that the chan0 and chan1 in the filename refer to the two polarizations at the feed, but the SNR is similar and strong enough to decode in each polarization, so it is enough to look at one of them. There is another recording done 10 minutes later, but it contains signals similar to this one.
The waterfall of the moment when the LEV-1 signal first appears is plotted using Inspectrum and shown here (click on the image to view it in full size). Two things stand out. First, there is noticeable fading. This is the only significant fading in this recording, but the second recording also shows some signal strength changes. This would be difficult to explain if LEV-1 was completely stationary on the Moon’s surface, and suggests that the hopper was moving.

The second unusual thing is that there is amplitude shift keying in the signal. This signal is in fact a typical PCM/PSK/PM signal, but the residual carrier is amplitude shift keyed with what looks like Morse code. Modulating the residual carrier in this way is highly unusual, because the residual carrier is supposed to be a stable phase reference for the demodulation of the signal, so shift-keying its amplitude doesn’t look like a great idea. The low-level amplitude of the residual carrier (which corresponds to the gaps between the dits and dahs) is very low, and the carrier almost disappears in the waterfall.
The telemetry subcarrier has a frequency of 2048 Hz and a symbol rate of 64 baud. This frequency zoom level is too low to see the modulation, so the telemetry subcarrier appears like a CW carrier at either side of the residual carrier. Its power level changes somewhat due to the amplitude shift keying of the residual carrier, but these power changes are much smaller than those of the residual carrier. Additionally, when the residual carrier is in the low-amplitude level, the second harmonic of the telemetry subcarrier is well visible in the waterfall.
Despite the amplitude shift keying on the residual carrier, it turns out a PLL can do a good job at tracking the phase of the residual carrier. I’m using a rather narrow PLL bandwidth of 5 Hz, which is quite reasonable for a UHF signal. I am using the following GNU Radio flowgraph to demodulate the PCM/PSK/PM telemetry signal and also to extract the amplitude data from the residual carrier.
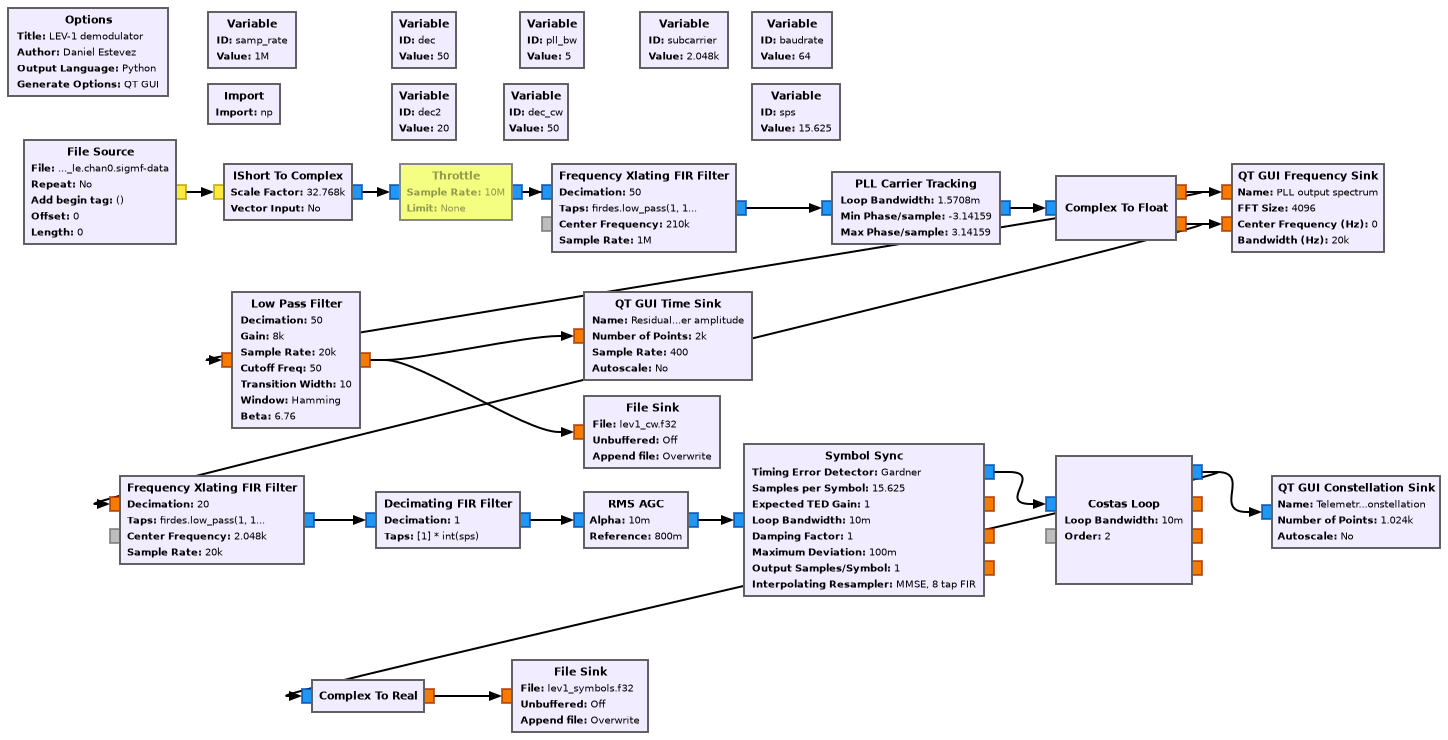
This is what the GUI of the demodulator shows when running with this recording. Since the telemetry is only 64 baud, the constellation plot with this SNR is excellent. Note the second harmonic of the telemetry subcarrier, which appears in the in-phase component. This is typical when the subcarrier zero-crossings are smooth instead of instantaneous, since the smooth zero-crossings modulate the residual carrier amplitude.
After arriving to this point, I tried to determine the CCSDS coding without success. I used my typical approach of correlating the symbols against each of the CCSDS syncwords, and also performing Viterbi decoding for each of the possible variations of the CCSDS code and then correlating against the 32-bit syncword. I also tried to look at the autocorrelation of the symbols, but this didn’t yield any patterns.
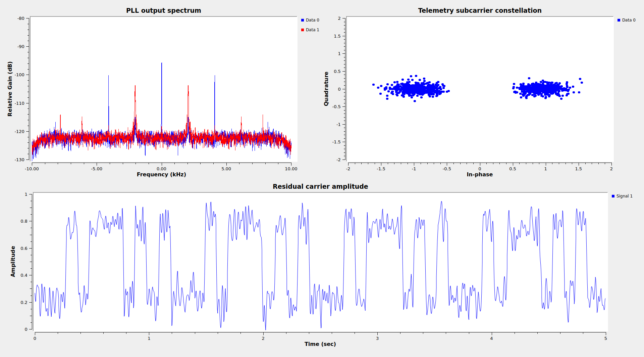
Since none of this worked but the clue of 32 bits per second mentioned in the IARU coordination sheet compared with the 64 baud symbol rate strongly suggested the presence of convolutional coding, I did some more work to check if this signal was convolutionally encoded. I used the BCJR decoder that I had done for Voyager I with each of the 4 possible variants of the CCSDS code (two possible orders for the polynomials, plus an optional bit inversion in one of the encoder branches), as well as the two possible pairings of symbols. The nice thing about a BCJR decoder in comparison to a Viterbi decoder is that its output is LLRs (log-likelihood ratios). If the decoder is set for the wrong code, the LLRs will look like a mess, but if the decoder is set for the correct code, the LLRs will form a clean “constellation” that avoids values around zero. Of all the combinations tested, the CCSDS/NASA-GSFC convention with no inversion in one of the branches gave good LLRs, as shown here.
The output of the BCJR validated that I had found the correct convolutional code, and provided the decoded stream of bits. Still, I couldn’t find any syncword in this stream, and the autocorrelation didn’t shown any patterns. Plotting the bits as a raster map with an arbitrary width gave a randomly looking image. This made me suspect that the signal was scrambled with an asynchronous scrambler, so I tried a to descramble it using a few common algorithms, and then looked at the raster map again.
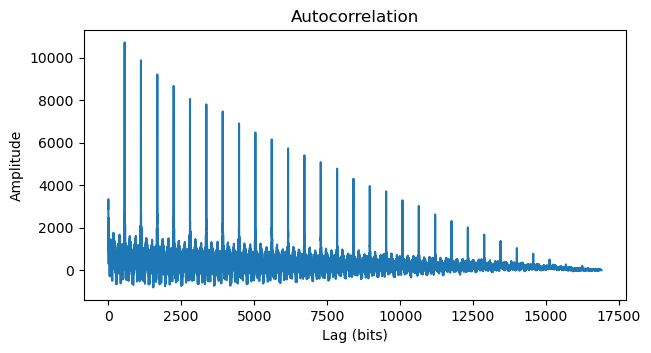
The G3RUH descrambler gave something that still looked random, but the Intelsat IESS-308 descrambler gave something that looked promising. The output had long runs of zeros (after correcting for a polarity inversion caused by the BPSK 180 degree phase ambiguity). Moreover, the autocorrelation of the descrambled bits showed very large peaks at a lag of 560 bits and its integer multiples.
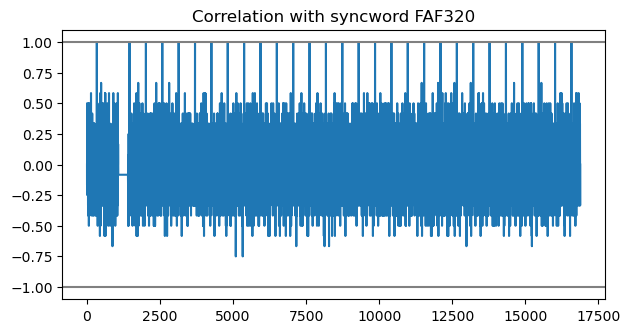
Still, no trace of any of the CCSDS syncwords. I plotted the raster map of the bits using a width of 560 bits, and noticed that some of the columns of this raster map looked like what could be a syncword. Writing these columns in hex gave 0xAAAAFAF320. The 0xAAAA part is just a series of alternating ones and zeros. The kind of thing that you would use as a preamble to train a receiver clock. But the 0xFAF320 part is a commonly used syncword. I know that it is used in CCSDS Proximity-1 (I mentioned this recently in my post about the MOVE-II cubesat), but apparently it is also used in IRIG 106. A Google search for “FAF320 syncword” reveals many results. Of special interest is this NASA report, which lists all the CCSDS syncwords, as well as the HDLC 0x7e flag (which I had also tried to search in the stream of bits), and mentions the relation between 0xFAF320 and IRIG.
Indeed, correlating the stream of descrambled bits with the syncword 0xFAF320 reveals peaks every 560 bits. There is an exception to this, which is the first and second peak. They are at a distance of 1120 bits. I think that the explanation is that the first frame was of a different type, which was twice the length of the other frames.
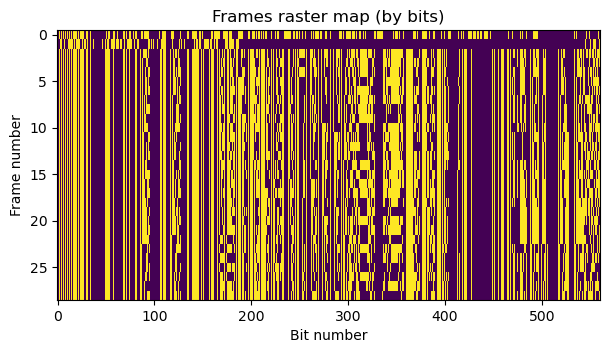
The next figure shows the raster map of the bits in each frame. The width of the raster map is 560 bits, so the first two rows should be understood as the first frame, which is twice as long. It is apparent that it has a different format compared to the other frames. Its final part is all zeros. The remaining frames have all the same format, and fields that line up are apparent.
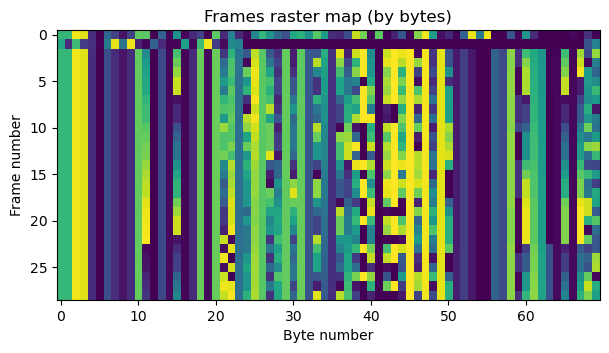
The following figure is the same kind of raster map, but with bytes instead of bits. Here it is clear that there are some telemetry fields that have increasing values. Some of these fields are 16-bit wide, because when a byte overflows, the previous byte increments by one. The last 2 bytes might be a CRC-16, but I haven’t managed to find the algorithm (there are many possible algorithms, and it is not clear if the preamble or syncword should be included in the CRC calculation).
I haven’t reverse engineered the telemetry data beyond this. It is not so easy, since there isn’t much telemetry to try to find patterns, and it doesn’t seem to follow CCSDS protocols. It would be great to have more documentation about the telemetry from the LEV-1 team, specially since this spacecraft is using the amateur satellite service and has gone through an IARU coordination process (in which one of the questions is whether technical documentation about the telemetry will be publicly available).
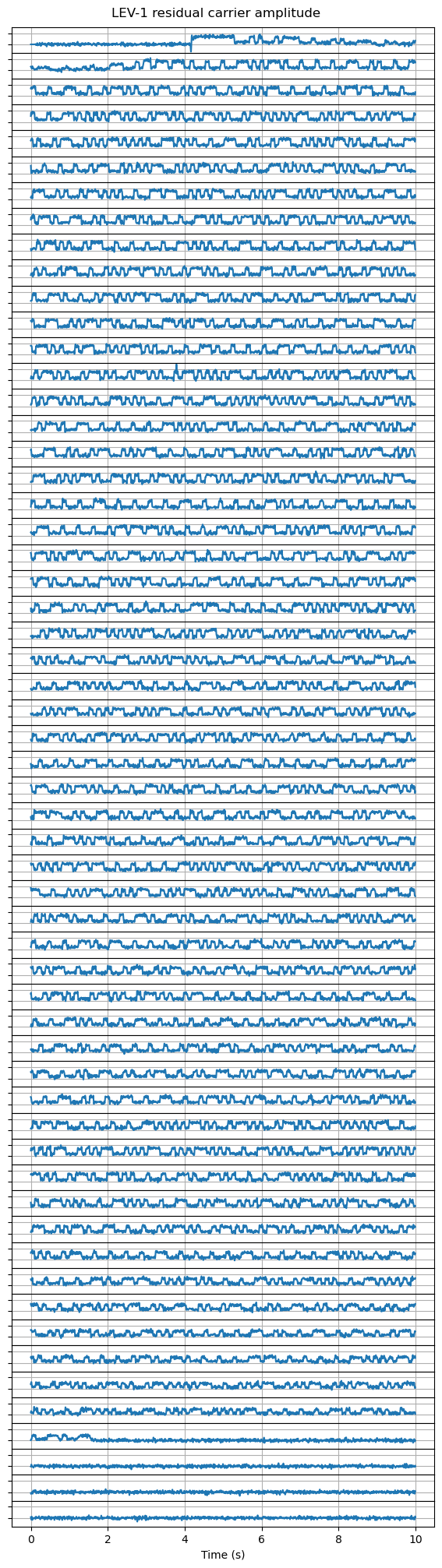
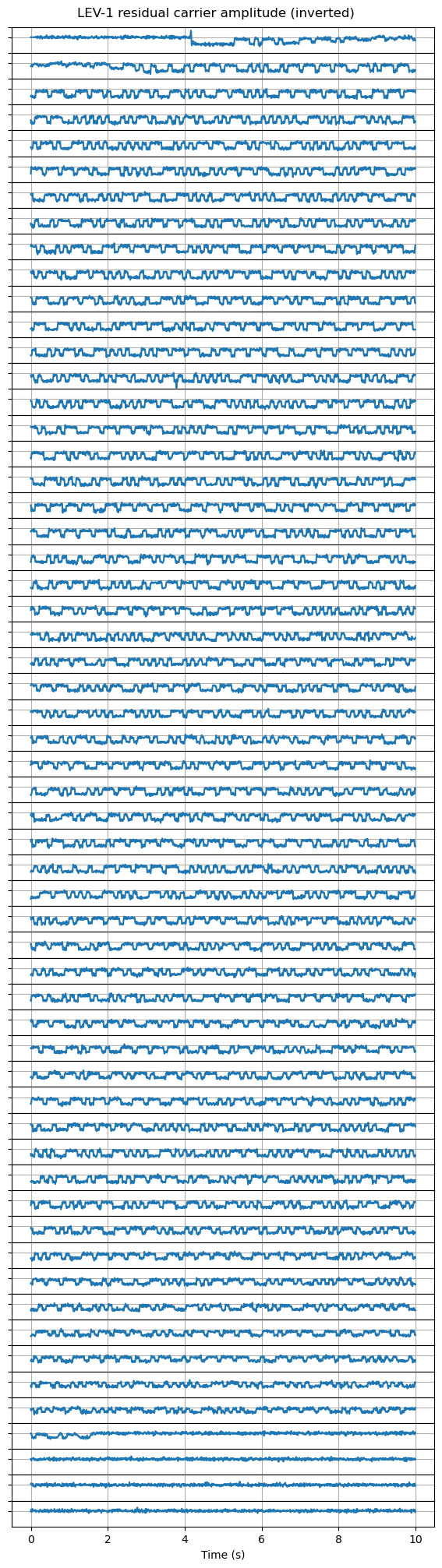
Now let us turn our attention at the Morse code modulating the residual carrier in amplitude. The next figure shows the amplitude of the residual carrier throughout all the recording. Each 10 second segment is represented as one trace in the plot. The plot should be read left to right and top to bottom as if it was text. To me it is clear that this is intended to be Morse code, as opposed to digital amplitude-shift-keying. All the runs of low levels and high levels appear to be have length 1 or 3, which is what happens in Morse. A digital ASK modulation would typically have runs of other lengths. The IARU coordination sheet also mentions “CW morse beacon contains housekeeping data”.
Despite being almost sure that this is Morse, it looks like nonsense to me. Many regular characters can be recognized, but there are also some strange sequences that might be rare prosigns (-….-.. and …-…. for instance). I have seen that other satellites transmit binary data in hexadecimal in Morse, but this doesn’t seem to be the case. Maybe some other radio amateurs can find the meaning of this, or perhaps someone from the LEV-1 team can tell us what this means.
In summary, what I have found about the LEV-1 437.41 MHz telemetry is that it is PCM/PSK/PM with a symbol rate of 64 baud and 2048 kHz subcarrier. The residual carrier is modulated in amplitude with Morse code. The telemetry signal is convolutionally encoded using the CCSDS/NASA-GSFC and no inversion in one of the encoded branches (correction: the convolutional code has inversion in one of the branches, so it is exactly as the code recommended by CCSDS; see update below). There is IESS-308 scrambling before the convolutional encoding. The frames have a 0xAAAA preamble followed by the syncword 0xFAF320. However, the contents of the frames and the meaining of the Morse code data are unknown.
The GNU Radio flowgraphs and Jupyter notebooks used in this post, as well as the intermediate data files can be found in this repository.
Update: Norbert DL8LAQ has figured out how to read the Morse code. It turns out that it is inverted: the dahs and dits are represented by a low amplitude on the residual carrier, and the gaps by a high amplitude. I don’t know what was the reasoning behind this, since when one listens to the residual carrier, what is heard would be the opposite of what one expects. Perhaps it was intended to listen the Morse code off the second harmonic of the telemetry subcarrier, for which the dahs and dits correspond to high amplitude levels.
Here is the same plot as above, but with the sign of the amplitude inverted. Now it is clear what Norbert says: the transmission is CQ CQ DE JS1YMG” followed but a lot of hexadecimal data. The gaps between words are the same length as the gaps between letters, but otherwise this is perfectly readable Morse.
Update 2024-01-22: Scott Chapman K4KDR has found that the last two bytes of the frames are indeed a CRC-16. The CRC algorithm is CRC-16-CCITT-FALSE (see this online calculator), but there is the catch that the data included in the CRC calculation starts 3 bytes after the 0xFAF320 syncword. The three bytes that must be skipped are 0x003e20 in all the frames. This is probably some sort of header. This only applies to the 560 bit frames. I haven’t been able to find a way to validate the CRC of the first frame in the recording, which appears to be a 1120 bit frame (and the three bytes after its syncword are 0x005632 instead). I have updated the Jupyter notebook to include the CRC check, showing that all the frames except this first longer frame have a valid CRC.
Update 2024-03-06: I have realized that the convolutional code does have inversion in one of the branches. The reason why I thought there was no inversion is because my BCJR decoder had the inversion logic incorrectly labelled: it was always doing an inversion (since it was adapted from a Voyager-1 decoder, which needs this), and then it was doing an additional inversion when inversion was enabled. I have realized this when updating the GNU Radio decoder to include a Viterbi decoder. The GNU Radio decoder flowgraph now has two Viterbi decoders (one for each possible pairing of input symbols) followed by IESS-308 descramblers, and the output of these is saved to a file.