
The other day I was thinking, could I make a certain plot in Lego? Well, Let's start at the start and make a simple n*m lego-brick. The basic measurements are:
brickstyle=Sequence[Red,EdgeForm[AbsoluteThickness[1]]];
gropts=Sequence[Boxed->False,ViewVector->(10{2.4, -1.3, 2.}),ViewAngle->8*Degree];
dims={dimx,dimy,dimz}={8.0,8.0,9.6}/8; (* size of a unit cell in lego-world *)
knobd=4.8/8; (* knob diameter *)
knobh=1.8/8; (* knob height *)
botdi=4.8/8; (* bottom pillar inner diameter*)
botdo=6.51/8; (* bottom pillar outer diameter*)
wall=1.2/8; (* wall thickness*)
thickness=1.0/8; (* top thickness *)
And here a function that will make simple brick:
ClearAll[DrawLego]
DrawLego[{nx_Integer,ny_Integer,nz_Integer:1},detailed:(True|False|None):True]:=Module[{ptsout,ptsin,sides,bottom,rimi,rimo,knobs,knobs2},
ptsout=Tuples[{{0,0,0},{nx,ny,nz}dims}\[Transpose]];
ptsin=Tuples[{{wall,wall,0},{nx,ny,nz}dims-{wall,wall,thickness}}\[Transpose]];
sides=If[BooleanQ[detailed],If[TrueQ[detailed],{ptsin,ptsout},{ptsout}],{ptsout}];
sides=GraphicsComplex[#,{Polygon[{1,2,6,5}],Polygon[{3,4,8,7}],Polygon[{1,2,4,3}],Polygon[{5,6,8,7}],Polygon[{2,4,8,6}]}]&/@sides;
If[TrueQ[detailed],
ptsout=Tuples[{{0,0,0},{nx,ny,0}dims}\[Transpose]];
ptsin=Tuples[{{wall,wall,0},{nx,ny,nz}dims-{wall,wall,thickness}}\[Transpose]];
rimo=ptsout[[1;;;;2]][[{1,3,4,2}]];
rimi=ptsin[[1;;;;2]][[{1,3,4,2}]];
rimo=Partition[rimo,2,1,1];
rimi=Partition[rimi,2,1,1];
bottom=MapThread[Polygon[#1~Join~Reverse[#2]]&,{rimo,rimi}];
];
If[BooleanQ[detailed],
knobs=Tuples[Range[1,#]&/@({nx,ny})]-1/2;
knobs=Cylinder[{Append[#{dimx,dimy},nz dimz],Append[#{dimx,dimy},nz dimz+knobh]}&/@knobs,knobd/2];
];
If[TrueQ[detailed],
knobs2=Tuples[Range[1,#]&/@({nx,ny}-1)];
knobs2=Tube[{Append[#{dimx,dimy},0],Append[#{dimx,dimy},nz dimz-thickness]}&/@knobs2,botdo/2];
];
If[BooleanQ[detailed],
If[TrueQ[detailed],
{sides,bottom,knobs,{CapForm[None],knobs2}}
,
{sides,knobs}
]
,
{sides}
]
]
DrawLego[{nx_Integer,ny_Integer,nz_Integer:1},p:{px_,py_,pz_},detailed_:True]:=Translate[DrawLego[{nx,ny,nz},detailed],p{1,1,dimz}-{0.5,0.5,0}]
So we can draw any brick now, at any place, and we have the option to have it detailed or not...
Graphics3D[{brickstyle, DrawLego[{4, 2}]}, Lighting -> "Neutral", Boxed -> False, Axes -> True]
Graphics3D[{brickstyle, DrawLego[{4, 2, 1}]}, Lighting -> "Neutral", Boxed -> False, Axes -> True]
Graphics3D[{brickstyle, DrawLego[{4, 2, 1}, {1, 1, 1}]}, Lighting -> "Neutral", Boxed -> False, Axes -> True]
Graphics3D[{brickstyle, DrawLego[{4, 2, 1}, {1, 1, 1}, False]}, Lighting -> "Neutral", Boxed -> False, Axes -> True]
Graphics3D[{brickstyle, DrawLego[{4, 2, 1}, {1, 1, 1}, None]}, Lighting -> "Neutral", Boxed -> False, Axes -> True]
giving:

So now that we can 'plot' any brick we can make a function that will cover a layer in brick-world with bricks of decreasingly smaller sizes iteratively, and will alternately go in the horizontal x and y directions:
ClearAll[TileWithLego,CreateLegos,TransformLego]
TileWithLego[slice_List/;MatrixQ[slice],sizes_List,greedy:(True|False),bricks_List:{}]:=Module[{size,bounds,sizex,sizey,shift,dims,dimx,dimy,greedy\[Lambda],stepi,stepj,newarr,part,newbricks},
size={sizex,sizey}=First[sizes];
dims={dimy,dimx}=Dimensions[newarr=slice];
shift=Floor[First[size]/2];
{stepi,stepj}=If[greedy,{1,1},{sizex,sizey}];
greedy\[Lambda]=Boole[!greedy];
newbricks=Reap[Do[
bounds={{j,j+sizey-1},{i,i+sizex-1}};
part=Take[newarr,##]&@@bounds;
If[Total[part,2]===sizex sizey,
newarr[[Span@@bounds[[1]],Span@@bounds[[2]]]]=0;
Sow[bounds];
]
,
{j,1,dimy-sizey+1,stepj}
,
{i,1+greedy\[Lambda] Mod[(j-1)/sizey,2]shift,dimx-sizex+1,stepi}
]][[2]];
If[newbricks==={},newbricks={{}}];
newbricks=bricks~Join~newbricks[[1]];
If[Length[sizes]>1,
TileWithLego[newarr,Rest[sizes],greedy,newbricks]
,
Reverse/@newbricks
]
]
CreateLegos[slice_List/;MatrixQ[slice],sizes_List,rotate:(True|False),greedy:(True|False)]:=If[rotate,Reverse/@TileWithLego[slice\[Transpose],sizes,greedy],TileWithLego[slice,sizes,greedy]]
TransformLego[slices_List,bricks_List,greedy:(True|False|Automatic)]:=Module[{len,greedies,heights,rotates,brickies,brickspec},
len=Length[slices];
heights=Range[len];
rotates=(#=!=0)&/@Mod[heights,2];
greedies=Switch[greedy,True,ConstantArray[True,len],False,ConstantArray[False,len],_,Switch[len,1,{False},2,{False,False},_,{False,False}~Join~ConstantArray[True,len-2]]];
brickies=MapThread[CreateLegos[#1,bricks,#2,#3]&,{slices,rotates,greedies}];
brickspec=MapThread[{#1[[All,All,2]]-#1[[All,All,1]]+1,{#1[[All,All,1]],ConstantArray[#2,Length[#1]]}\[Transpose]}\[Transpose]&,{brickies,heights}];
brickspec=Catenate[brickspec];
brickspec[[All,2]]=Flatten/@brickspec[[All,2]];
brickies=DrawLego[#1,#2,False (* detailed *)]&@@@brickspec;
{Graphics3D[{brickstyle,brickies},Boxed->False,ImageSize->700],brickspec}
]
Let's turn a simple plot in to its Lego-presentation:
heightmap=Table[8+Round[3.5Sin[0.1(0.1x^2+y)]/1.2],{x,-15,24,2},{y,-30,28,2}];
ListPlot3D[%,Mesh->None,InterpolationOrder->0]
minmax=MinMax[heightmap]+0.5{-1,1};
slices=UnitStep[heightmap-#+1]&/@Range@@minmax;
{gr,bricks}=TransformLego[slices,{{4,2},{3,2},{2,2},{4,1},{3,1},{2,1},{1,1}},Automatic];
gr
giving:
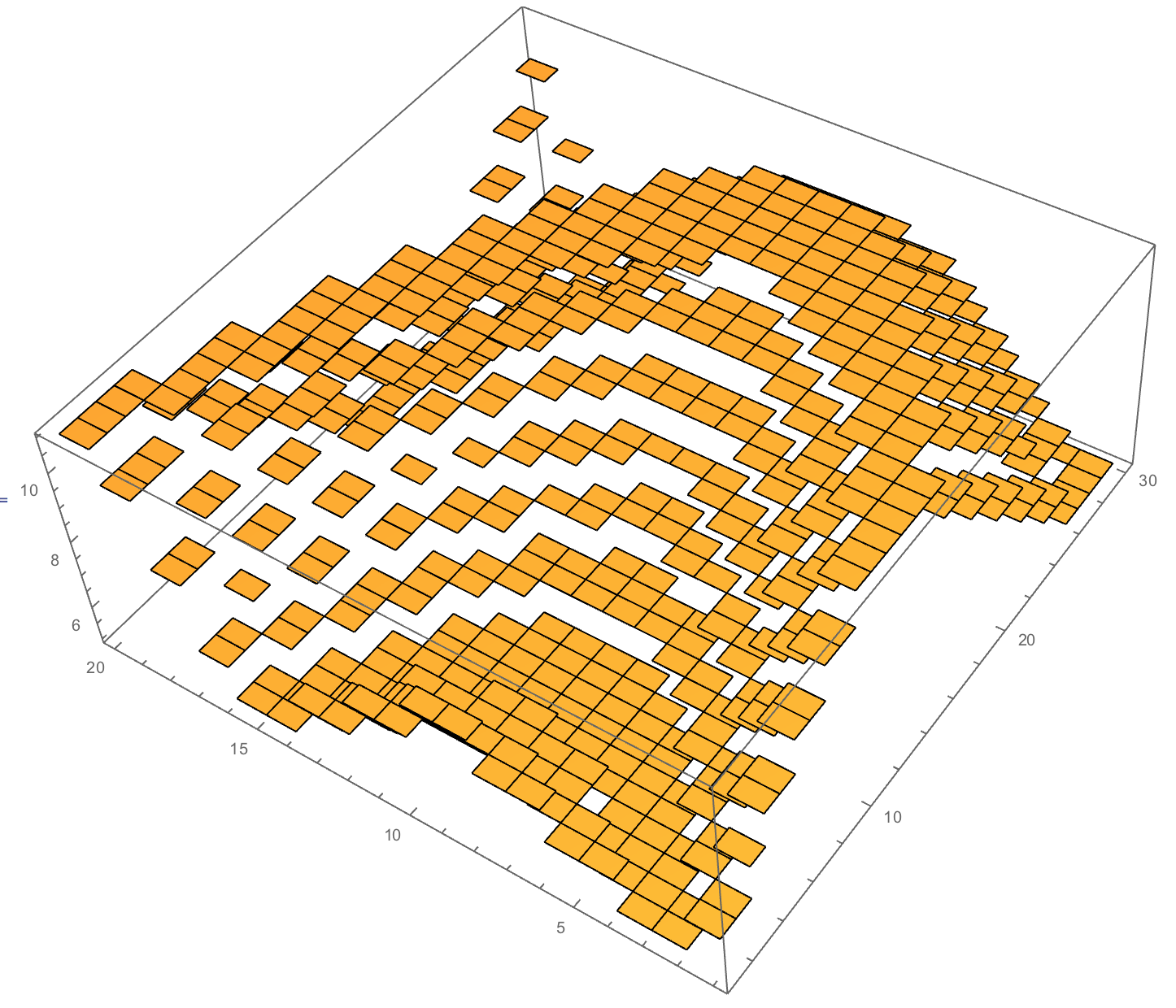

We can try different shapes, namely a sphere:
slices=DiskMatrix[{9/dimz,9,9},20];
{gr,bricks}=TransformLego[slices,{{4,2},{3,2},{2,2},{4,1},{3,1},{2,1},{1,1}},Automatic];
gr

Or a pyramid:
slices=DiamondMatrix[{8,8,8},18][[10;;]];
{gr,bricks}=TransformLego[slices,{{4,2},{3,2},{2,2},{4,1},{3,1},{2,1},{1,1}},Automatic];
gr

The price (according to the online lego shop), would be:
prices = {{2, 4} -> 0.23, {1, 2} -> 0.11, {1, 1} -> 0.08, {1, 3} -> 0.15, {1, 4} -> 0.15, {2, 2} -> 0.15, {2, 3} -> 0.19};
Total[(Sort /@ bricks[[All, 1]]) /. prices]
18.76
We can go now and make some instructions for making this pyramid! Because I can't build something without instructions. Let's create some layer-by-layer instructions:
ClearAll[CreatePage,CreatePages]
CreatePage[slices_List,pagenumber_Integer]:=Module[{add,old,image,gr,gr3,opts,width=500},
{add,old}=TakeDrop[slices,-1];
image=(DrawLego[#1,#2,False]&@@@#)&/@slices;
add=Flatten[add,1];
add=SortBy[Minus@*First][Reverse/@Tally[Sort/@add[[All,1]]]];
add[[All,1]]=Style[Row[{#,"\[Cross]"}],16,Black]&/@add[[All,1]];
add[[All,2]]=Graphics3D[{brickstyle,DrawLego[#]},gropts,ImageSize->50,Background->None]&/@add[[All,2]];
add=Grid[add];
gr3=Graphics3D[{brickstyle,image},Boxed->False,ViewPoint->(10{2.4, -1.3, 2.}),ImageSize->2width/3];
gr=Graphics[
{LightBlue,Rectangle[{0,0},{1,1.5}],
Inset[gr3,Scaled@{0.5,0.5}],
Inset[Style[ToString[pagenumber],30,Black],Scaled@{0.5,0.05},Scaled@{0.5,0}],
Inset[add,Scaled@{0.05,1},Scaled@{0,1}]
},
Axes->False,
Frame->False,
ImageSize->(width{1,1.5}),
PlotRange->{{0,1},{0,1.5}},
AspectRatio->Full
]
]
CreatePages[bricks_List]:=Module[{brickslices,out},
brickslices=SortBy[Part[#,1,-1,-1]&][GatherBy[bricks,Part[#,-1,-1]&]];
out = Map[CreatePage[brickslices[[;;#]],#]&,Range[Length[brickslices]]];
Rasterize[#,"Image"]& /@ out
]
So let's call the function:
CreatePages[bricks]
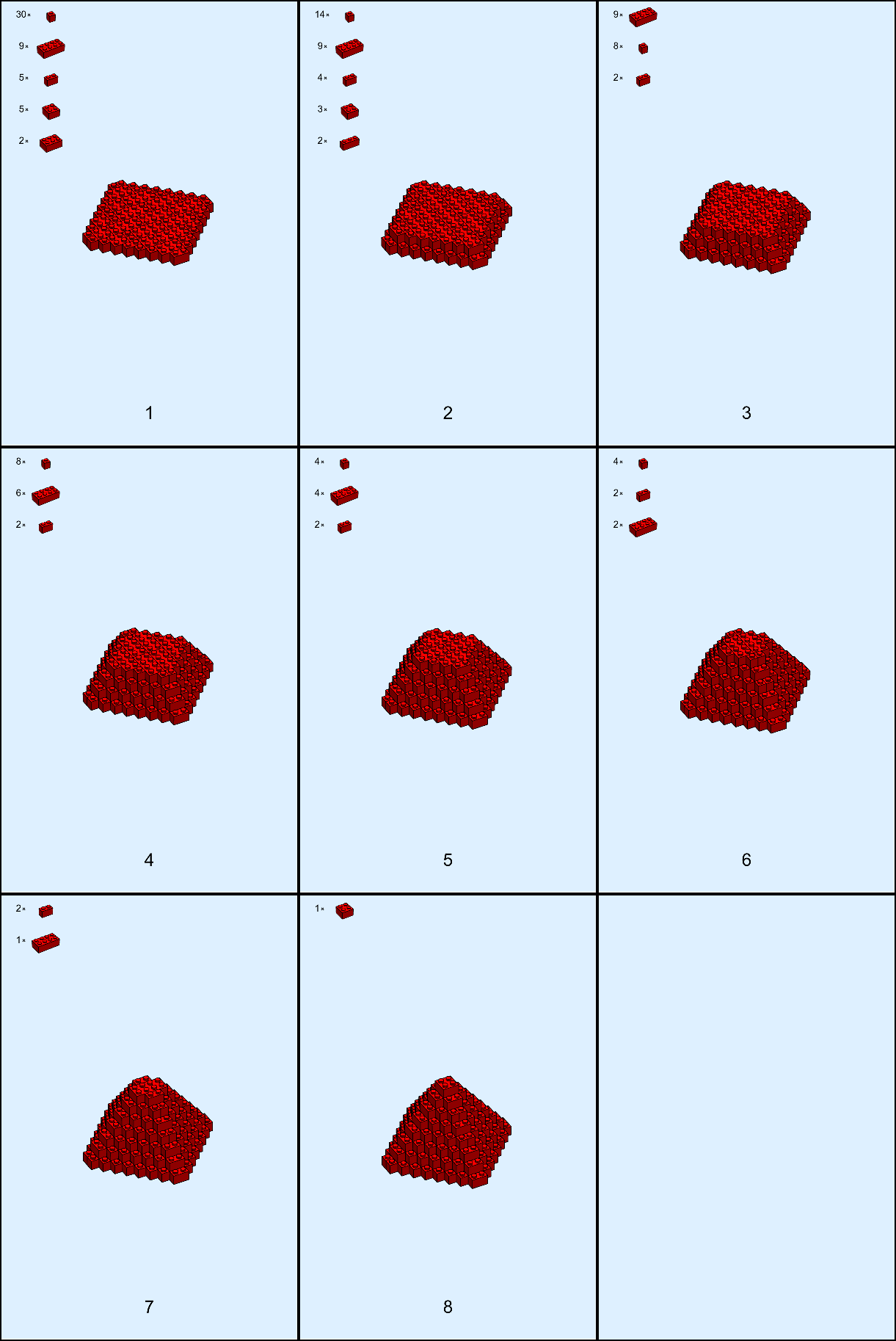
gives me back 8 pages of instructions, including the bricks I need for that 'layer' !
Lastly, let's make one from a 3D model:
brickstyle=Sequence[RGBColor[0.55,0.38,0.19],EdgeForm[AbsoluteThickness[1]]];
bg=ExampleData[{"Geometry3D","Triceratops"},"BoundaryMeshRegion"]
bounds={xbounds,ybounds,zbounds}=CoordinateBounds[ExampleData[{"Geometry3D","Triceratops"},"VertexData"]];
rmf=RegionMember[bg];
\[Delta]=2^-3;
alldata=Boole[Table[rmf[{x,y,z}],{x,xbounds[[1]],xbounds[[2]],\[Delta]},{y,ybounds[[1]],ybounds[[2]],\[Delta]},{z,zbounds[[1]],zbounds[[2]],\[Delta]}]];
alldata=Transpose[alldata,{3,2,1}];
{gr,bricks}=TransformLego[alldata,{{4,2},{3,2},{2,2},{4,1},{3,1},{2,1},{1,1}},False];
gr

Now feel free to turn your own plots, 3d-scans, and models to Legos!
