Coding The Matrix - NFHN Reader

Coding The Matrix: Linear Algebra Through Computer Science Applications

About The Course

The course has been taught at Brown University since 2008, and is being taught in Fall 2017. Slides from past editions of the Brown University course are available here.
A shortened version has been taught through Coursera. The aim of this course is to provide students interested in computer science an introduction to vectors and matrices and their use in CS applications.

The course is driven by applications from areas chosen from among: computer vision, cryptography, game theory, graphics, information retrieval and web search, and machine learning.

Course Resources

Data and support code required for carrying out the assignments are provided here.

Auto-grading is made available for some of the tasks.

Here are the first and second labs from Edition One. These have nothing to do with linear algebra. They are provided to bring the reader up to speed in the part of Python we use in the book. Here is a document intended to assist people with making the transition from loops to comprehensions.

Join the mailing list for updates about addition of resources.

Slides

Slides from the course taught at Brown University in Fall 2013:

Sign up for updates

To receive messages when new material is available, e.g. blog posts about applications of linear algebra to CS, news of a follow-on course, or corrections to the book, join the mailing list. I promise that mailings will be rare and that I will not share your email address with anybody, ever.

About The Book

Example Applications

Here are examples of applications addressed in Coding the Matrix.

crossfade

A line segment between points is given by the convex combinations of those points; if the "points" are images, the line segment is a simple morph between the images.
Perspective rectification

Given a photo of a whiteboard taken at an angle, synthesize a perspective-free view of the whiteboard.

The same transformation can be used in using a Wiimote to make a low-cost interactive whiteboard or light pen (due to Johnny Chung Lee).
Error-correcting codes

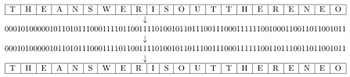
Error-correcting codes are used, e.g., by cellphones to preserve data transmitted over a noisy channel while maintaining high throughput.
Integer factorization
522253825433285668885771662040104167 = 891428822186035241∙585861498344390287
Factoring an integer is a hard computational problem (and the RSA cryptosystem depends on it being hard). At the core of the most sophisticated integer-factoring algorithms is a simple problem in linear algebra.
Image blurring

Blurring an image is a simple linear transformation.
Searching within an audio clip

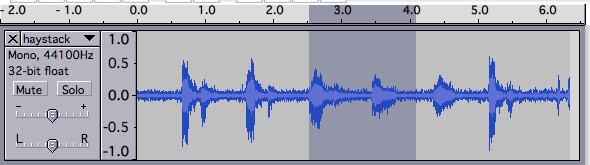
Searching for one audio clip within another can be formulated as a convolution. A convolution can be computed very quickly using the Fast Fourier Transform.
Searching within an image

Convolution can also be done in two dimensions, enabling one to quickly search for a subimage within an image.
Audio and image compression
Compression of audio and images aids efficient storage and transmission. Lossy compression techniques such as those used in MP3 (audio) and JPEG (images) are based in part on linear algebra,
e.g. wavelet transform and Fourier transform.

100% original size

40% original size

10% original size
Face detection

A "classical" approach to face detection is eigenfaces, a technique related to principal component analysis.
2d graphics transformations

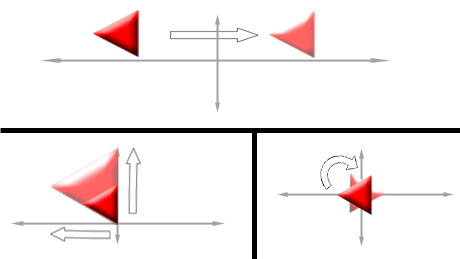
Simple transformations that arise in graphics such as rotation, translation, and scaling can be expressed using matrices.
Lights Out

Lights Out is a puzzle in which you must select the correct buttons to push in order for all the lights to go out. Finding a solution can be expressed as a problem in linear algebra.
Minimum-weight spanning forest

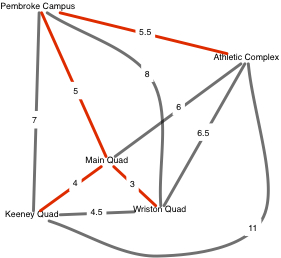
Finding the minimum-weight spanning tree of a graph can be interpreted as the problem of finding a minimum-weight basis for a vector space
derived from the graph.
Graph layout

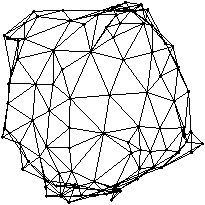
A nice drawing of a graph can be obtained from eigenvectors of a related matrix.