Last Updated : 8 Oct, 2025
Given the root of a binary tree, Find its inorder traversal using Morris Traversal, i.e., without using recursion or a stack.
Examples:
Input:
Output: [4, 2, 5, 1, 3]
Explanation: Inorder traversal (Left->Root->Right) of the tree is 4, 2, 5, 1, 3.Input:
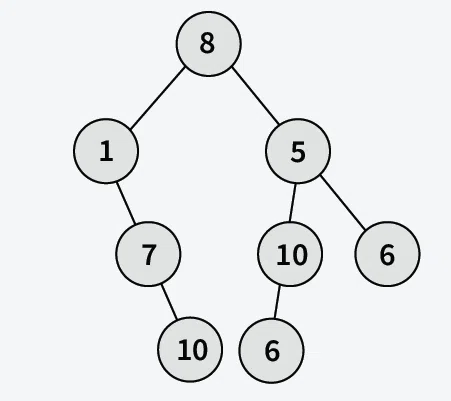
Output: [1, 7, 10, 8, 6, 10, 5, 6]
Explanation: Inorder traversal (Left->Root->Right) of the tree is 1, 7, 10, 8, 6, 10, 5, 6.
Try it on GfG Practice
Approach:
We want to traverse the tree and come back to the root after finishing the left subtree, but without a stack. Morris Traversal achieves this by temporarily modifying the tree:
- For each node, check if it has a left child.
- If it does not have a left child, visit it and move to the right child.
- If it has a left child, find the inorder predecessor (rightmost node in the left subtree).
Make the current node as the right child of its inorder predecessor (temporary link).
Move to the left child. - When you encounter a temporary link again, it means the left subtree is fully visited:
Remove the temporary link.
Visit the current node.
Move to the right child.
#include <iostream>
#include <vector>
using namespace std;
// Node Structure
class Node {
public:
int data;
Node* left;
Node* right;
Node(int x) {
data = x;
left = right = nullptr;
}
};
vector<int> inOrder(Node* root) {
vector<int> res;
Node* curr = root;
while (curr != nullptr) {
if (curr->left == nullptr) {
// If no left child, visit this node
// and go right
res.push_back(curr->data);
curr = curr->right;
}
else {
// Find the inorder predecessor of curr
Node* prev = curr->left;
while (prev->right != nullptr &&
prev->right != curr) {
prev = prev->right;
}
// Make curr the right child of its
// inorder predecessor
if (prev->right == nullptr) {
prev->right = curr;
curr = curr->left;
}
else {
// Revert the changes made in
// the tree structure
prev->right = nullptr;
res.push_back(curr->data);
curr = curr->right;
}
}
}
return res;
}
int main() {
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
vector<int> res = inOrder(root);
for (int data : res) {
cout << data << " ";
}
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100000
// Node Structure
struct Node {
int data;
struct Node* left;
struct Node* right;
};
int* inOrder(struct Node* root, int* size) {
struct Node* curr = root;
int capacity = MAX_SIZE;
int* res = (int*)malloc(capacity * sizeof(int));
int count = 0;
while (curr != NULL) {
if (curr->left == NULL) {
// If no left child, visit this node
// and go right
if (count >= capacity) {
capacity *= 2;
res = (int*)realloc(res, capacity * sizeof(int));
}
res[count++] = curr->data;
curr = curr->right;
}
else {
// Find the inorder predecessor of curr
struct Node* prev = curr->left;
while (prev->right != NULL && prev->right != curr) {
prev = prev->right;
}
// Make curr the right child of its
// inorder predecessor
if (prev->right == NULL) {
prev->right = curr;
curr = curr->left;
}
else {
// Revert the changes made in
// the tree structure
prev->right = NULL;
if (count >= capacity) {
capacity *= 2;
res = (int*)realloc(res, capacity * sizeof(int));
}
res[count++] = curr->data;
curr = curr->right;
}
}
}
// set the size
*size = count;
return res;
}
// Helper to create a new node
struct Node* createNode(int data) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
int main() {
// Binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
struct Node* root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5);
int size;
int* res = inOrder(root, &size);
for (int i = 0; i < size; i++) {
printf("%d ", res[i]);
}
free(res);
return 0;
}
import java.util.ArrayList;
// Node Structure
class Node {
int data;
Node left, right;
Node(int x) {
data = x;
left = right = null;
}
}
class GFG {
static ArrayList<Integer> inOrder(Node root) {
ArrayList<Integer> res = new ArrayList<>();
Node curr = root;
while (curr != null) {
if (curr.left == null) {
// If no left child, visit this node
// and go right
res.add(curr.data);
curr = curr.right;
}
else {
// Find the inorder predecessor of curr
Node prev = curr.left;
while (prev.right != null &&
prev.right != curr) {
prev = prev.right;
}
// Make curr the right child of its
// inorder predecessor
if (prev.right == null) {
prev.right = curr;
curr = curr.left;
}
else {
// Revert the changes made in
// the tree structure
prev.right = null;
res.add(curr.data);
curr = curr.right;
}
}
}
return res;
}
public static void main(String[] args) {
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
ArrayList<Integer> res = inOrder(root);
for (int data : res) {
System.out.print(data + " ");
}
}
}
# Node Structure
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def inOrder(root):
res = []
curr = root
while curr is not None:
if curr.left is None:
# If no left child, visit this node
# and go right
res.append(curr.data)
curr = curr.right
else:
# Find the inorder predecessor of curr
prev = curr.left
while prev.right is not None \
and prev.right != curr:
prev = prev.right
# Make curr the right child of its
# inorder predecessor
if prev.right is None:
prev.right = curr
curr = curr.left
else:
# Revert the changes made in the
# tree structure
prev.right = None
res.append(curr.data)
curr = curr.right
return res
if __name__ == "__main__":
# Representation of input binary tree:
# 1
# / \
# 2 3
# / \
# 4 5
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
res = inOrder(root)
for data in res:
print(data, end=" ")
using System;
using System.Collections.Generic;
// Node Structure
class Node {
public int data;
public Node left, right;
public Node(int x) {
data = x;
left = right = null;
}
}
class GFG {
static List<int> inOrder(Node root) {
List<int> res = new List<int>();
Node curr = root;
while (curr != null) {
if (curr.left == null) {
// If no left child, visit this
// node and go right
res.Add(curr.data);
curr = curr.right;
}
else {
// Find the inorder predecessor of curr
Node prev = curr.left;
while (prev.right != null
&& prev.right != curr) {
prev = prev.right;
}
// Make curr the right child of its
// inorder predecessor
if (prev.right == null) {
prev.right = curr;
curr = curr.left;
}
else {
// Revert the changes made in
// the tree structure
prev.right = null;
res.Add(curr.data);
curr = curr.right;
}
}
}
return res;
}
static void Main(string[] args) {
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
List<int> res = inOrder(root);
foreach (int data in res) {
Console.Write(data + " ");
};
}
}
// Node Structure
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function inOrder(root) {
let res = [];
let curr = root;
while (curr !== null) {
if (curr.left === null) {
// If no left child, visit this
// node and go right
res.push(curr.data);
curr = curr.right;
}
else {
// Find the inorder predecessor of curr
let prev = curr.left;
while (prev.right !== null
&& prev.right !== curr) {
prev = prev.right;
}
// Make curr the right child of its
// inorder predecessor
if (prev.right === null) {
prev.right = curr;
curr = curr.left;
}
else {
// Revert the changes made in the
// tree structure
prev.right = null;
res.push(curr.data);
curr = curr.right;
}
}
}
return res;
}
// Driver Code
// Representation of input binary tree:
// 1
// / \
// 2 3
// / \
// 4 5
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
let res = inOrder(root);
console.log(...res);
Time Complexity: O(n), if we take a closer look, we can notice that every edge of the tree is traversed at most three times.
Auxiliary Space: O(1)