$\begingroup$
"The best card trick", an article by Michael Kleber. Here is the opening paragraph:
"You, my friend, are about to witness the best card trick there is. Here, take this ordinary deck of cards, and draw a hand of five cards from it. Choose them deliberately or randomly, whichever you prefer--but do not show them to me! Show them instead to my lovely assistant, who will now give me four of them: the 7 of spades, then the Q of hearts, the 8 of clubs, the 3 of diamonds. There is one card left in your hand, known only to you and my assistant. And the hidden card, my friend, is the K of spades."
$\endgroup$
8
$\begingroup$
This was fascinating for me. Somehow the man takes a bagel and with one cut arrives with two pieces that are interlocked. Whether this qualifies as "magic" I dunno (it's hard to say once the trick's been explained), but it sure seems like it to me.
It doesn't hurt that I love bagels, and have the opportunity to perform this with friends/family/non-math people and can teach a little about problems/topology/counter-intuitive facts about the universe.
$\endgroup$
5
$\begingroup$
Five unrelated items:
Mobius strip
One of the best mathematical tricks is what happens when you cut a Mobius strip in the middle. (Look here) (And what happens when you cut it again, and when you cut it not in the middle.) This is truly mind boggling and magicians use it in their acts. And it reflects deep mathematics.
Diaconis mind reading trick
I also heard from Mark Gorseky this description of a mathematical based card game
"Mark described a card trick of Diaconis where he takes a deck of cards, gives it to a person at the end of the room, lets this person “cut” the deck and replace the two parts, then asks many other people do the same and then asks people to take one card each from the deck. Next Diaconis is trying to read the mind of the five people with the last cards by asking them to concentrate on the cards they have. To help him a little against noise coming from other minds he asks those with black cards to step forward. Then he guesses the cards each of the five people have.
Mark said that Diaconis likes to perform this magic with a crowd of magician since it violates the basic rule: “never let the cards out of your control”. This trick is performed (with a reduced deck of 32 cards) based on a simple linear feedback shift register. Since all the operations of cuting and pasting amount to cyclic permutations, the 5 red/black bits are enough to tell the cylic shift and no genuine mind reading is required."
I think there is a paper by Goresky and Klapper about a version of this magic and relations to shift registers.
The Link Illusion
I heard a wonderful magic from Nahva De Shalit. You tie a string between the two hands of two people and link the two strings. The task is to get unlinked.
This ties with what I heard from Eric Demaine about the main principle behined many puzzles (Some of which he manufectured with his father whan he was six!)
Symmetry Illusion
Sometimes things are not as symmetric as they may look.
commutators-based magic
(I heard this from Eric Demaine and from Shahar Mozes.) If we hang a picture (or boxing gloves) with one nail, once the nail falls so does the picture. If we use two nails then ordinarily if one nails falls the picture can still hangs there. Mathematics can come for the rescue for the following important task: use five nails so that if any one nail falls so does the picture.

$\endgroup$
7
$\begingroup$
I saw this trick demonstrated at a math camp once. When it works, it is extremely impressive to non-mathematicians and mathematicians alike.
Have a volunteer shuffle a deck of cards, select a card, show it to the audience, and shuffle it back into the deck. Take the deck from him, and fling all of the cards into the air. Grab one as it falls, and ask the volunteer if it is his card.
1 in 52 times (this is the deep mathematics part), the card you grab will be the card the volunteer selected. Even most statisticians should be amazed at this feat. Just make sure you never perform this trick twice to the same audience.
$\endgroup$
4
$\begingroup$
Persi Diaconis and Ron Graham just published Magical Mathematics. The book contains a plethora of magic tricks rooted in deep mathematics.
$\endgroup$
1
$\begingroup$
The following trick uses some relatively deep mathematics, namely cluster algebras. It will probably impress (some) mathematicians, but not very many laypeople.
Draw a triangular grid and place 1s in some two rows, like the following except you may vary the distance between the 1s:
1 1 1 1 1 1 1
. . . . . .
. . . . . . .
. . . . . .
. . . . . . .
. . . . . .
1 1 1 1 1 1 1
Now choose some path from the top row of 1s to the bottom row and fill it in with 1s also, like so:
1 1 1 1 1 1 1
1 . . . . .
. 1 . . . . .
1 . . . . .
. 1 . . . . .
. 1 . . . .
1 1 1 1 1 1 1
Finally, fill in all of the entries of the grid with a number such that for every 2 by 2 "subsquare"
b
a d
c
the condition $ad-bc=1$ is satisfied, or equivalently, that $d=\frac{bc+1}{a}$. You can easily do this locally, filling in one forced entry after another. For example, one might get the following:
1 1 1 1 1 1 1
1 2 3 2 2 1
. 1 5 5 3 1 .
1 2 8 7 1 .
. 1 3 11 2 1 .
. 1 4 3 1 .
1 1 1 1 1 1 1
The "trick" is that every entry is an integer, and that the pattern of 1s quickly repeats, except upside-down. If you were to continue to the right (and left), then you would have an infinite repeating pattern.
This should seem at least a bit surprising at first because you sometimes divide some fairly large numbers, e.g. $\frac{5\cdot 11+1}{8} = 7$ or $\frac{7\cdot 3+1}{11} = 2$ in the above picture. Of course, the larger the grid you made initially, the larger the numbers will be, and the more surprising the exact division will be.
Incidentally, if anyone can provide a reference as to why this all works, I'd love to see it. I managed to prove that all of the entries are integers, and that they're bounded, and so there will eventually be repetition. However, the repetition distance is actually a simple function of the distance between the two rows of 1, which I can't prove.
$\endgroup$
4
$\begingroup$
$\endgroup$
1
$\begingroup$
A late addition: The Fold and One-Cut Theorem. Any straight-line drawing on a sheet of paper may be folded flat so that, with one straight scissors cut right through the paper, exactly the drawing falls out, and nothing else. Houdini's 1922 book Paper Magic includes instructions on how to cut out a 5-point star with one cut. Martin Gardner posed the general question in his Scientific American column in 1960.
For the proof, see Chapter 17 of Geometric Folding Algorithms: Linkages, Origami, Polyhedra. We include instructions for cutting out a turtle, which, in my experience, draws a gasp from the audience. :-)
$\endgroup$
$\begingroup$
The coffee mug trick
Give a coffee mug (full if you're brave) to someone and ask them to rotate 360 degrees without spilling the (real or imaginary) coffee, so that their hand ends up in the same position.
This is impossible, so you get to smirk while they contort themselves and become more and more baffled (this works better with more than one person since it turns into a kind of "competition")
Finally, take the cup and show that while it's impossible to turn it once (as has been "proven"), it's possible to turn it twice (!) and end up in the same position.
Has to do with the fundamental group of SO(3) being $\mathbb{Z}/2\mathbb{Z}$, and when we require the cup to stay upright we end with a non-trivial loop.
$\endgroup$
4
$\begingroup$
Here is a general trick that you can use to make yourself look like you have an amazing memory.
Start with a finite abelian group $(G,+)$ in which you are comfortable doing arithmetic. Be sure to know the sum $$g^* = \sum_{g \in G} g.$$
Take a set $S$ of $|G|$ physical objects with an easily computable set isomorphism $$ \varphi : S \longrightarrow G.$$ Allow your audience to remove one random element from $a \in S$ and then shuffle $S$ without telling you what $a$ is. [Shuffling means we need $G$ to be abelian.]
Now inform your audience that you are going to look briefly at each remaining element of $S$ and remember exactly which elements you saw, and determine by process of elimination which element of $S$ was removed.
Now glace through all the remaining elements of $S$ one by one and keep a "running total" to compute $$ \varphi(a) = g^* - \sum_{s \in S-\{a\}} \varphi(s).$$
Finally apply $\varphi^{-1}$ and obtain $a.$
Note that $\varphi$ is not "canonical" in the sense there are definitely choices to be made. On the other hand in should be "natural" in the sense that you should be very comfortable saying $s = \varphi(s).$
The prototypical example is to take $G$ to be $\Bbb Z / 13 \Bbb Z \times V_4,$ $S$ to be a standard deck of 52 cards, and $\varphi(s)$ to be $( \text{rank}(s) , \text{suit}(s) )$.
$\endgroup$
4
$\begingroup$
Audience asked to choose an integer from 0 to 1000. Ask to give remainder when divided by 7, 11, and 13 respectively.
Magician gives original integer by Chinese Remainder Theorem.
Works because 7×11×13=1001.
$\endgroup$
0
$\begingroup$
$\endgroup$
1
$\begingroup$
A puzzle based on Hamming codes discussed here: is the following:
A room contains a normal 8×8 chess board together with 64 identical coins, each with one “heads” side and one “tails” side. Two prisoners are at the mercy of a typically eccentric jailer who has decided to play a game with them for their freedom. The rules are the game are as follows.
The jailer will take one of the prisoners (let us call him the “first” prisoner) with him into the aforementioned room, leaving the second prisoner outside. Inside the room the jailer will place exactly one coin on each square of the chess board, choosing to show heads or tails as he sees fit (e.g. randomly). Having done this he will then choose one square of the chess board and declare to the first prisoner that this is the “magic” square. The first prisoner must then turn over exactly one of the coins and exit the room. After the first prisoner has left the room, the second prisoner is admitted. The jailer will ask him to identify the magic square. If he is able to do this, both prisoners will be granted their freedom
$\endgroup$
4
$\begingroup$
You can use hamming codes to guess a number with lying allowed. For example, here is a way to guess a number 0-15 with 7 yes-or-no questions, and the person being questioned is allowed to lie once. (The full cards are here).
$\endgroup$
1
$\begingroup$
I would like to thank all the contributors on this page. I have been putting together a new Math-a-Magic show for the 9-12 grade level and have found some fantastic material here. If I get a decent video of the show I'll be sure to post a link here so you can play the "What concept is behind this trick?" game.
I have modified some of your ideas severely. For example. Craig Feinstein's suggestion was a commercial effect that asks the volunteer to pick one of a hundred different cities typed out on ten cards. The volunteer finds the city's name on two different cards which the magician looks at casually. You can then instantly tell him the name of the city he has mentally picked.
In my version, I instruct him not to ever let me see the city's name on the cards and yet I can still easily predict his choice!
Here is my favorite trick based on the deep principal of Set theory. Ok, maybe it is not too deep but the results are astounding!
Taking a deck of cards, you mention you have a prediction about these cards. That means it is very important to give the cards a really random shuffle. You then give your volunteer half the deck and you both shuffle your half decks thoroughly. Tell your volunteer to take a small amount(5-15) of cards from his half of the deck, turn them upside down and give them to you. you do the same to him (doesn't matter how many cards you turn upside down as long as there is some left in your hand) You then both shuffle the cards you have received into the deck in your hands in there upside down state. so at this point both people will have some cards right side up some cards upside down. You will follow the same procedure two more times. It doesn't matter how many or what cards he or you are turning upside down and giving away. After all this is done put both half decks of cards together again (IMPORTANT: turn your entire half deck over when you place it on top of his) Now you spread the cards out across a table top. They should be a seemingly random mix of upside down and rigtside up cards. You then unfold your prediction slip which says something like: 11 cards will be black, 15 cards will be red, 6 will be clubs and 5 will be hearts and the hearts will also form a royal Flush!
They will be astounded by your amazingly detailed prediction. What happens is that all the face up cards are the ones that were originally in your half deck. This trick is self working. All you do is to pick out which cards you want in your half of the deck and place them at the top of the deck to start. Then just give him the random bottom half of the deck and you keep the pre-set ones.
Any questions? Just email me at [email protected]
$\endgroup$
$\begingroup$
Here is a card trick from Edwin Connell's Elements of Abstract and Linear Algebra, page 18 (it can be found online). I always do this trick to my undergraduate number theory class in the first minutes of the first day. A few weeks later, after they've learned some modular arithmetic, we come back to the trick to see why it works. I quote from Connell:
"Ask friends to pick out seven cards from a deck and then to select one to look at without showing it to you. Take the six cards face down in your left hand and the selected card in your right hand, and announce you will place the selected card in with the other six, but they are not to know where. Put your hands behind your back and place the selected card on top, and bring the seven cards in front in your left hand. Ask your friends to give you a number between one and seven (not allowing one). Suppose they say three. You move the top card to the bottom, then the second card to the bottom, and then you turn over the third card, leaving it face up on top. Then repeat the process, moving the top two cards to the bottom and turning the third card face up on top. Continue until there is only one card face down, and this will be the selected card."
When I do this trick, I always use big magician's cards (much easier for an audience to see), but a regular deck works too. To get to the trick faster, I skip the first part and just pick 7 cards myself, showing them all the cards so they see nothing is funny (like two ace of spades or something). I then spread the cards in one hand face-down and let a student pick one and show it to everyone else but me before I take it back face down. When the student is showing the cards to the class I move the rest of the cards behind me so that before I get the card back I already have the rest behind my back.
You need to make sure students at the side of the room won't be able to see what you're doing behind your back (namely, putting the mystery card on the top of the deck), so stand close to the board. Practice this with yourself many times first to be sure you can do it without screwing up. The hard part is remembering to keep the last card you reached in the count on the top of the deck; that same card will be used when you start the count in the next round. If you stick it on the bottom before counting off cards again then you'll mess everything up. For instance, if someone picks the number 3 then I start counting from the top of the deck and say (with hand movements in brackets) "One [put it under], two [put it under], three [turn it over, put it on top FACE UP and stop]. This [show face-up card to everyone] is not your card. [Put it back face-up on top] One [now put it under], two [put it under], three [turn over and put on top FACE UP and stop]. This etc. etc."
Connell advises telling people to pick up a number from 1 to 7 but not allow 1. In practice there's no need to tell people not to pick 1. They never do (it's never happened to me). They don't pick 7 either. And if they did pick 1, well, just turn over the top card and you're done! Again, that never really happens.
$\endgroup$
4
$\begingroup$
The coffee mug trick is also called the Philipine Wine Trick and should be related to the Dirac String Trick, which you can find by a web search, for example here and also in my presentation Out of Line, where rotations in 3-space are related to the Projective Plane.
A knot trick, I am not sure you would call it magic, has been shown to children and academics in many places. It requires a pentoil knot of width 20" (say 100cm) made of copper tubing, about 0.25" (7mm) diameter (made by a university workshop) shown in the following diagram, but without the arrows and labels:
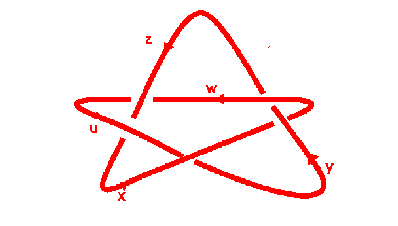
It also needs some nice flexible boating rope. The rope is wrapped round the $x,y$ pieces according to the rule $$R=xyxyxy^{-1}x^{-1}y^{-1}x^{-1}y^{-1} $$ and the ends tied together, as in the following picture:
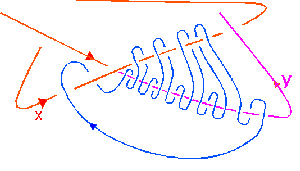
A member of the audience is then invited to come up and manipulate the loop of rope off the knot, starting by turning it upside down. This justifies the rule $R=1$. Of course the rule is the relation for the fundamental group of complement of the pentoil, which can, for the right audience, be deduced from the relations at each crossing given by the diagram

and can be easily demonstrated with the knot and rope. (The picture has no base point and so seems to me related more to the notion of fundamental groupoid than fundamental group.)
It is also of interest to have a copper trefoil rather than pentoil around to compare the relations. One warning: the use of rope does not really model the fundamental group or groupoid, so be careful with a demo for the figure eight knot!
I did the demo for one teenager and he said:"Where did you get that formula?" This demo knot has been well travelled, for many different types of audience; on one occasion the airline lost my luggage with the rope and I had to ask the taxi from the airport to to stop at a hardware store for me to buy d=some clothesline. I devised this trick for an undergraduate course in knot theory in the late 1970s.
You can also see a Knot Exhibition whose aim is to use the notion of knot to explain some basic methods of mathematics to the general public.
$\endgroup$
$\begingroup$
Here is a simple trick based on group theory. Ask a person to choose four numbers from 1 to 9 and write them in a row on a piece of paper. Pause for a moment and then write a number on a piece of paper without letting the other person see what it is. Turn the paper over and place it on the table.
Now ask the person to choose two of the numbers from the list and put a line though them. Ask the person to compute a*b + a + b and put it in the list to replace the two chosen numbers.
Continue to do this until there is only one remaining number. Turn over the paper and show that the numbers match.
The simplest way of explaining this is to show that a * b + a + b is isomorphic to multiplication using the transform T(x) = x + 1. (a*b + a + b) + 1 = (a + 1)(b + 1). If we denote the operation a * b + a + b as a & b, this means that a & b is commuative and associative, just as multiplication is. For any list of numbers ai, the final number can be computed as the (a1 + 1)(a2 + 1)...(an + 1) - 1.
$\endgroup$
1
$\begingroup$
I gave a talk about card shuffling to a general audience recently and wanted to memorise a "random-looking" deck so as to motivate a correct definition of what it means for a deck to be random. Most magicians actually use memory tricks to learn off the deck but I thought it would be much cleverer to order the cards in the obvious way, and then find a recursive sequence of length 52 containing all of 1 to 52. In the end, caught for time I settled on using the Collatz recursive relation with seed 18 --- this allowed me to name off 21 distinct cards effortlessly and when I held up the deck prior to the demonstration, the audience voted that the deck was random. Can anyone think of a suitable recursive sequence with the desired property? We can either take a random-looking order and a "regular" recursive sequence but I think it would be much better to find an easy to compute recursive sequence that "looks random" when using a more canonical order simply because if we can remember a "random looking order" we're pretty much going to have to remember the whole deck --- the problem I'm exactly trying to avoid.
PS: I did one of the simpler Diaconis tricks. A deck is riffle shuffled three times, the top card shown to the audience, inserted into the deck, and after laying the cards out on the table the top card can be easily recovered by looking at the descents. The key is that the order of the deck is known beforehand --- a simple demonstration that three shuffles does not suffice to mix up a deck of cards (with respect to variation distance).
$\endgroup$
1
$\begingroup$
Ask someone to lay out the 52 cards in a deck, face up, in 4 rows of 13 cards each, in any order the person wants. Then you can always pick 13 cards, one from each column, in such a way as to get exactly one card of each denomination (that is, one ace, one deuce, ..., one king).
As a trick, it's not up there with sawing a woman in half, but its explanation does require Hall's Marriage Theorem.
$\endgroup$
6
$\begingroup$
Two persons, A and B, perform this trick. The public (or one from the public) chooses two natural numbers and give A the sum and B the product. A and B will ask each other, alternatively, the only single question "Do you know the numbers?" answering only yes or no until both find the numbers. There is a strategy such that for any input and only doing this, A and B will manage to find the original numbers.
I have never seen magicians actually performing this, but is perfectly doable.
This was a problem in the shortlist of the proposed problem for some international mathematical olympiad. Unfortunately I don't remember which. If someone remembers or finds it. Tell us please. i would also like to know.
$\endgroup$
8
$\begingroup$
Here's another Fibonacci trick, from Benjamin & Quinn's "Proofs that really count".
The magician hands a volunteer a sheet of paper with a table whose rows are numbered from one to ten, plus a final row for the total. She asks him to fill in the first two rows with his favorite two positive integers. She then asks him to fill in row three with the sum of the first two rows, row four with the sum of row two and row three, etcetera... She then hands him a calculator and asks him to add up all ten numbers together. Before he's able to finish that, the magician has a quick look at the sheet of paper and announces the total. The magician then asks the volunteer to divide row 10 by row 9, and cut up the answer to the second decimal digit. The volunteer performs the division and says: 1.61. And the magician: "Now turn over the paper and look what I've written". The paper says: "I predict the number 1.61".
The first part of the trick uses the following well-known Fibonacci identity:
$$\sum_{i=1}^nF_i=F_{n+2}-1$$
Indeed, call $x$ the number in row 1 and $y$ the number in row 2. Then for $n \geq 3$, the number in row $n$ is $F_{n-2} x+F_{n-1} y$, where $F_n$ is the $n$-th Fibonacci number. So the number in row 7 is $F_5 x + F_6 y=5x+8y$ and the total is $$x+y+\sum_{i=3}^{10} (F_{i-2} x+F_{i-1} y)= F_{10} x + F_{11} y=55x+88y$$ by the Fibonacci identity mentioned at the beginning. Therefore all the magician has to do to find the total is multiply row 7 by the number 11.
The second part of the trick uses an inequality for the freshman sum ;-) of two fractions. That is, given positive fractions $\frac{a}{b}$ and $\frac{c}{d}$ such that $\frac{a}{b}<\frac{c}{d}$ we have:
$$\frac{a}{b} < \frac{a+c}{b+d} < \frac{c}{d}$$
Just note that the number in row 9 is $13x+21y$ while the number in row 10 is $21x+34y$. Hence:
$$ 1.615 \dots =\frac{21x}{13x} < \frac{21x+34y}{13x+21y} < \frac{34y}{21y}=1.619 \dots $$
$\endgroup$
$\begingroup$
Not so much a magic trick as a math trick, in that I can prove it works in theory but I have never tried it in practice.
Take a very long one-dimensional frictionless billiard table, with a wall at one end. Away from the wall, place a billiard ball with mass $10^{2n}$ for $n$ positive. Between that ball and the wall, place another billiard ball with mass $1$. Then start the heavy ball rolling slowly towards the light one. Of course, they bounce, setting the light one traveling quickly towards the wall, which it bounces off, and then it hits the heavy ball, etc., until all the momentum from the heavy ball has been transferred and it starts rolling away.
Assume that all collisions are perfectly elastic. Then at the end of the day, there will be finitely many collisions. Indeed, the number of collisions will calculate the digits of $\pi$, in the sense that there will be $\lfloor \pi \times 10^n \rfloor$ collisions.
I prefer this method of calculating $\pi$ much better than the probabilistic one.
$\endgroup$
10
$\begingroup$
So two points of note.
I did not read all the posts above in detail but did do a search for the Faro Shuffle and got no results... So:
This is a shuffle where all the cards interweave absolutely perfectly (so a perfect riffle shuffle). There's quite a lot of maths behind this. For instance, 8 shuffles takes you back to the order you started shuffling the cards in. Martin Gardner talked about this a bit in at least one of his SA columns. The problem with the faro shuffle is it takes a long long time to learn... personally well over a year, and that was with the benefit of having been a practicing amateur magician for along time. Still if interested the book to look for is The Collected Works of Alex Elmsley, this really lays the foundations for mathematical faro work...
Another trick I came across whilst working towards an Ergodic Theory exam uses the Birkhoff Ergodic Theorem at its core. You can read about it in these notes: http://www.maths.manchester.ac.uk/~cwalkden/ergodic-theory/lecture22.pdf
Owen.
$\endgroup$
$\begingroup$
A recent episode of Penn and Teller's Fool Us had a trick by Hans Petter Secker which exploits the parity of a permutation in a lovely way. It may be useful the next time one has to teach the sign of a permutation!
Brief description of the trick in the video: The magician has sent a box over. Penn picks up a Rock from the box; Teller then picks Scissors from the box; and Alysson gets the remaining crumpled sheet of paper. The magician (on video) says that he will predict what they'll do (in the context of the Rock-Paper-Scissors game). He writes down a prediction, and invites Alysson to pick any two of them and swap their objects. The magician reveals his correct prediction. Next he writes down two predictions, and asks Teller to perform a swap, and then Penn to perform a swap (I might be forgetting who selects the swaps, but two swaps are made). Again the magician reveals his correct predictions. Finally he gets them to make three swaps. This time he has not written down any predictions, but when the crumpled paper is smoothed out, there are three correct predictions written on it. Enjoy!
$\endgroup$
0
$\begingroup$
Here's an example of a magic trick that works with high probability, based on a careful analysis of the riffle shuffle, in which an audience member performs a number of riffle shuffles and then moves a single card, and the magician guesses which card has been moved.
$\endgroup$
$\begingroup$
Peter Suber writes:
By the way, the single best knot trick I've ever found is at pp. 98-99 of Louis Kauffman's On Knots, a mathematical treatise listed below with the books on knot theory. I'm sure you've seen the trick in which someone ties an overhand knot by crossing their arms before picking up the cord, and then uncrossing them. Kauffman shows you how to do the same trick without crossing your arms first. The version of this trick in Ashley #2576 and Budworth 1977 [p. 151] is not nearly as good.
Work out how it is possible for yourselves! A link to the book is here.
[Edit: This magic trick does not rely on mathematics -- instead it violates an important mathematical fact, that the trefoil is not unknotted! The Chinese rings have a similar feel, but the mathematics violated (linking number) is less deep.]
$\endgroup$
6
$\begingroup$
Place $K$ faced-down cards on a table, blindfold yourself and ask him/her for a number $1 < n < K$. Allow him/her to flip $n$ random cards up. Cover the cards with an opaque box that has two holes for you to put your hands in and claim that you can split the cards into 2 stacks, each with same number of faced-up cards.
Based on a well known logic puzzle: http://usna.edu/Users/physics/mungan/_files/documents/Scholarship/CoinPuzzle.pdf Modified the process to make it harder for audience to figure out what you did and used cards so that they will not think that you did it by differentiating the surface of the coins.
$\endgroup$
$\begingroup$
I forgot the historical name for this and I'm pretty sure this is classical and well-known.
Consider a circular disk and remove an interior circular region, not necessarily concentric. In this annulus we play the following game. Start at any point $p_{1}$ of the outer boundary and draw a line through this point which is tangent to the inner circle. This line intersects the outer circle at another point $p_2$. Now repeat the same procedure with $p_2$ and get $p_3$. Iterating this procedure ad infinitum we either conclude that these sequence of points are periodic or not. What's true is that the periodicity or lack of it is independent of the starting point $p_1$.
I believe there is a proof involving Lefschetz fixed point theorem involving the torus but any details on this and the history of this is more than welcome.
$\endgroup$
3
$\begingroup$
Magician: "Here is a deck of 27 cards. Select one, memorize it, put it back and shuffle at libitum. Now name a number between 1 and 27 inclusive (=: N)." Then the magician deals the cards face up into three heaps. You have to tell him in which heap the selected card lies, and he quickly ramasses the three heaps. This is done three times, then he hands you the deck, and you have to count N cards from its back. The N'th card is flipped over, and it turns out to be the card you have originally selected.
$\endgroup$
You must log in to answer this question.
Explore related questions
See similar questions with these tags.